快速入手八大排序,带你从入门到精通
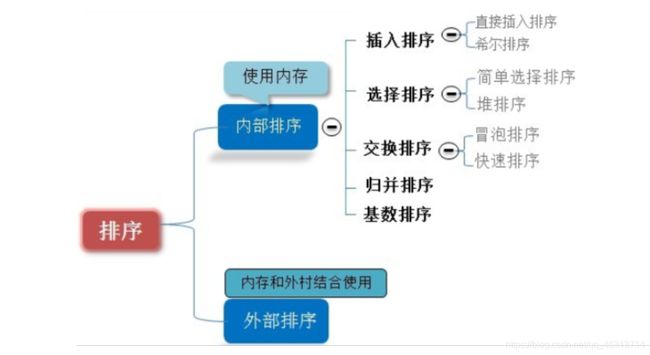
八大排序
- 冒泡排序
-
- 冒泡排序的优化:设立flag标志位。
- 选择排序
-
- 选择排序的优化:
- 直接插入排序
- 希尔排序(缩小增量的排序)
- 堆排
- 基数排序
- 快排
-
- 快排的递归做法
-
- 递归做法----hoare方法
- 递归做法------挖坑法
- 递归做法-----快慢指针方法
- 快排非递归写法
-
- 快排非递归方法---hoare方法。
- 快排非递归方法---挖坑法
- 快排非递归--快慢指针做法
- 快排的优化
-
- 取中间值法
- 利用插入排序来优化快排
- 快排的时间复杂度与空间复杂度及应用场景
- 归并排序
-
- 递归下的归并算法
- 非递归下的归并算法
- 归并排序与快速排序(快排)对比
- 巧记八大排序中各个算法稳定性
冒泡排序
冒泡排序定义:冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
动图演示:
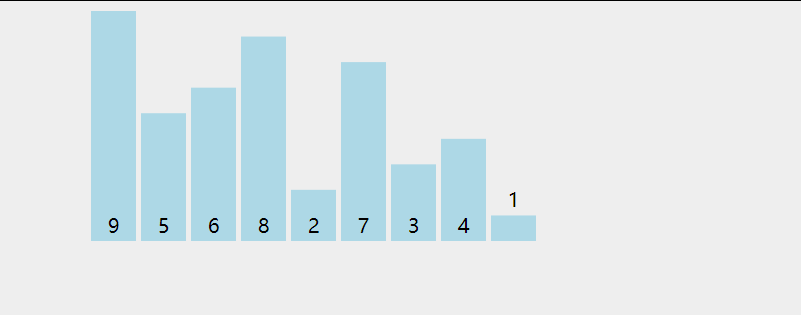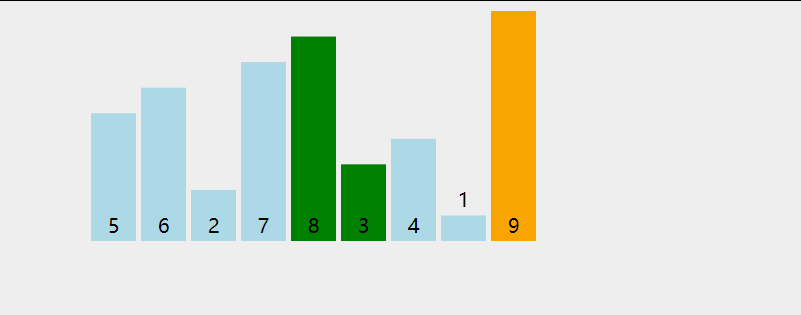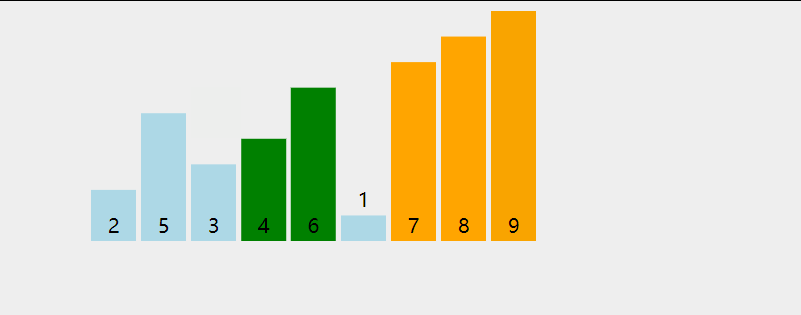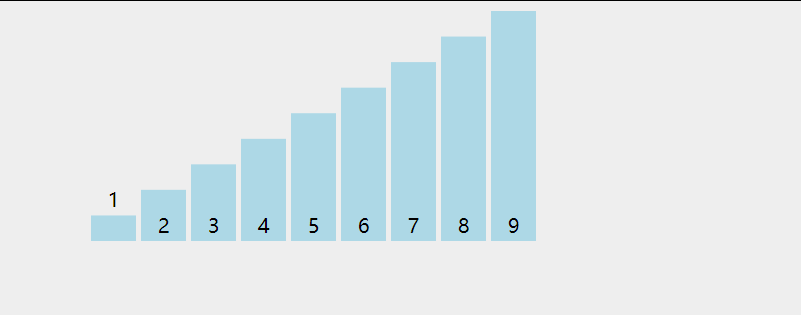
代码:
void bubble_sort(int arr[],int len)
{
for(int i=0;i<len-1;i++)//i控制趟数
{
for(int j=0;j<len-1-i;j++)//j控制比较到哪个元素截至,因为每次冒泡都可以选出最大的值,所以没必要每次走到数组尾再停。
{
if(arr[j]>arr[j+1])
{
swap(&arr[j],&arr[j+1]);
}
}
}
swap函数
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
冒泡排序的优化:设立flag标志位。
原因:冒泡排序每次冒泡都会选出该序列中的最大值或者最小值,若本次冒泡排序中没有任何元素交换的话,证明数组已经有序。避免了非必要的循环
int flag = 0;
for (int i = 0; i < len - 1; i++)
{
flag = 0;
for (int j = 0; j < len - 1 - i; j++)
{
if (arr[j] < arr[j + 1])
{
swap(&arr[j], &arr[j + 1]);
flag = 1;
}
}
if (flag == 0)
break;
}
算法稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
| 冒泡排序 | 对应的解 |
|---|---|
| 时间复杂度 | O(N^2) |
| 空间复杂度 | O(1) |
| 稳定性 | 稳定的(这块是不一定的,取决于自己判定条件,若判定条件写的是大于等于交换,则它不是稳定的) |
| 适用场景 | 适用于数据量较少的场景,数据量较多的话冒泡排序效率是很低的 |
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
动图演示:
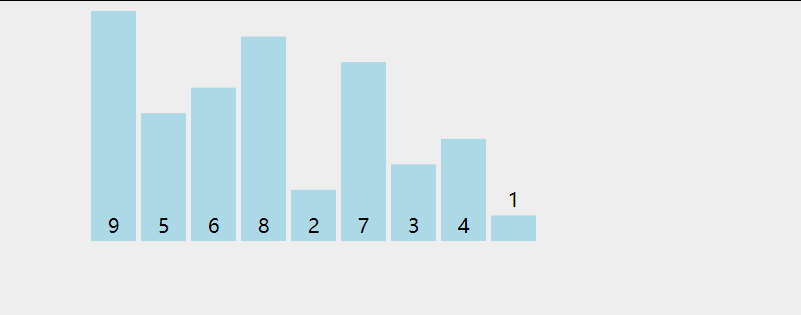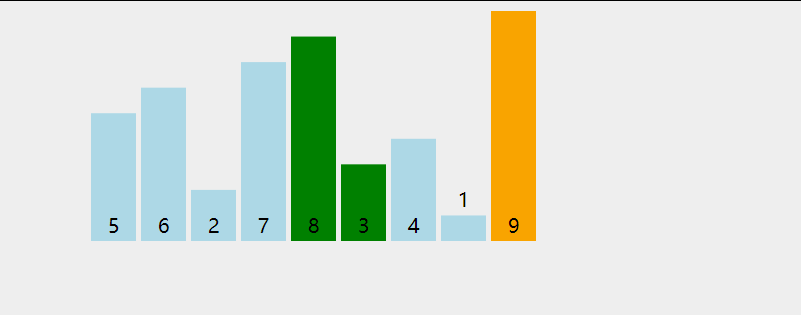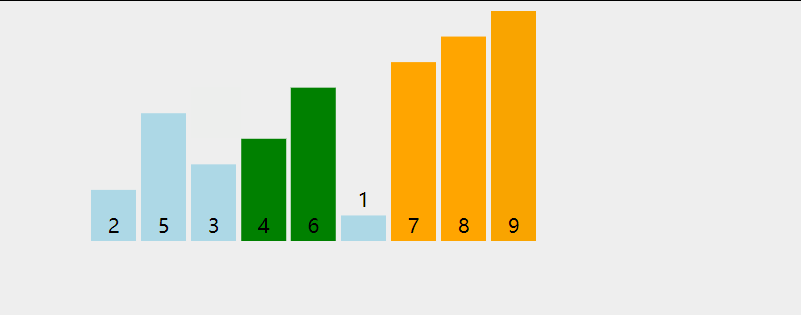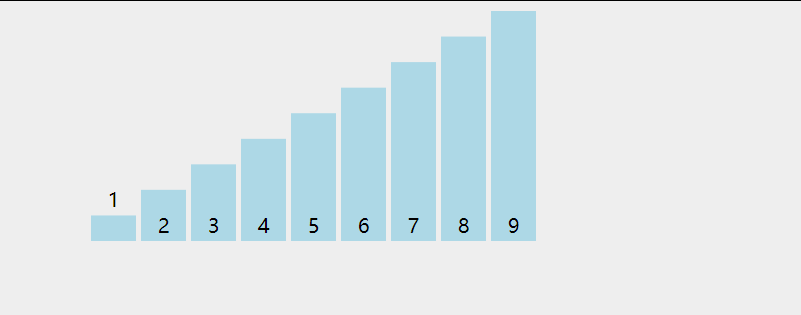
代码:
void select_sort(int arr[],int len)
{
for (int i = 0; i < len - 1; i++)
{
int max = i;
for (int j = i + 1; j < len; j++)
{
if (arr[max] < arr[j])
{
max = j;//更新max为最大元素的下标
}
}
if (max != i)
{
swap(&arr[i], &arr[max]);//swap函数如冒泡排序所示
}
}
}
选择排序的优化:
选择排序会出现很多次重复比较的情况,他每次都是象征性的给出一个最大元素的下标,然后做对比,比到最后一个,造成很大的程序开销,所以此次优化是为了减少比较的趟数,在每次遍历的基础上既选出最大的,又选出最小的。
void select_sort(int arr[],int len)
{
int left=0;
int right=n-1;
while(left<right)
{
int min=left;
int max=right;
for(int i=left;i<=right;i++)
{
if(arr[i]<arr[min]
min=i;
if(arr[i]>arr[max]
max=i;
}
if(min!=left)
{
swap(&arr[min],&arr[left]);
}
if(max!=right)
{
swap(&arr[max],arr[right]);
}
left++;
right--;
}
}
| 选择排序 | 对应的解 |
|---|---|
| 时间复杂度 | O(N^2) |
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
| 适用场景 | 适用于元素较少的情况 |
直接插入排序
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法 [1] 。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
动画演示:
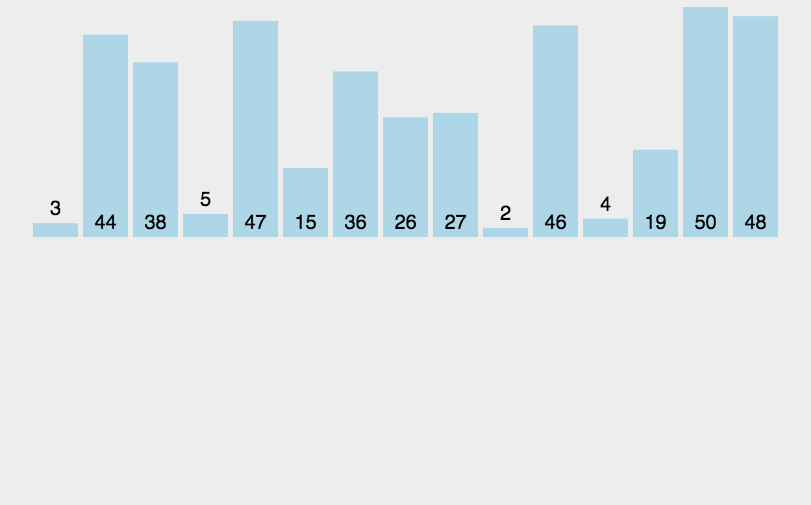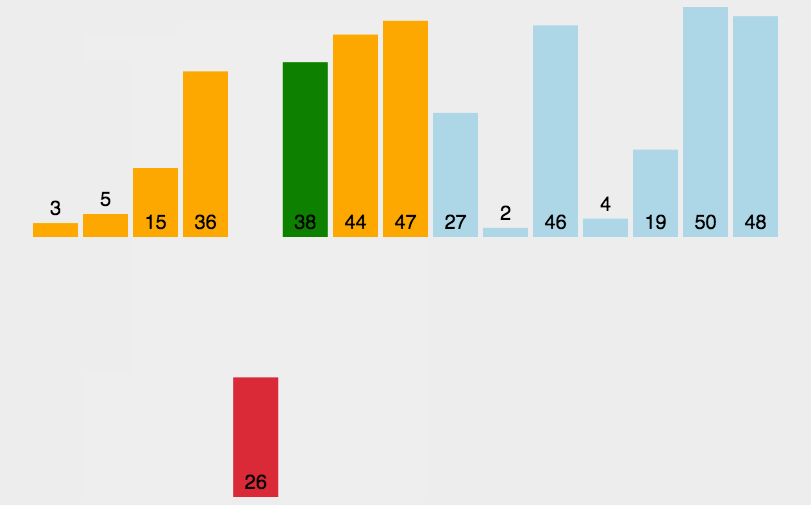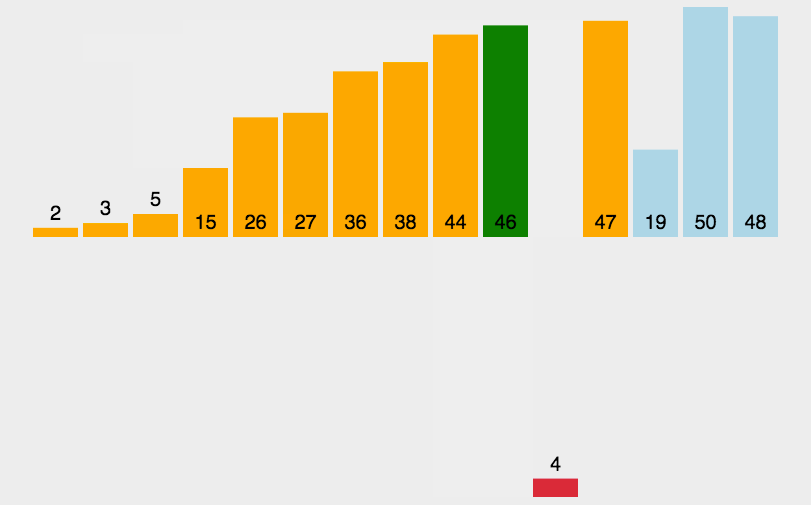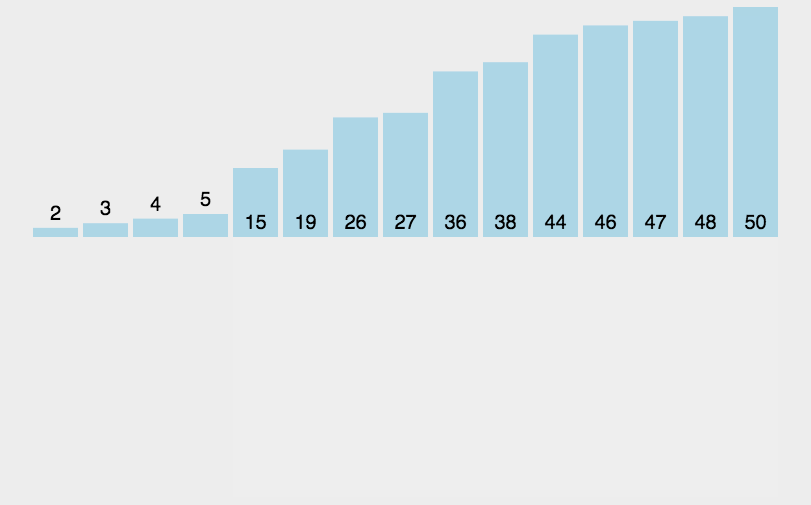
void insert_sort(int arr[],int len)
{
for (int i = 1; i < len; i++)
{
if (arr[i] < arr[i - 1])
{
int j = i - 1;
int temp = arr[i];
while (j >= 0 && temp < arr[j])
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = temp;
}
}
}
| 插入排序 | 对应的解 |
|---|---|
| 时间复杂度 | 最优的解O(N)(就意思是不需要走while语句,不需要移动元素,自身是已经排好序的),最差的是O(N^2)假设此时需要的刚好是原数组的逆序数组,这就比较裂开了。 |
| 空间复杂度 | O(1) |
| 稳定性 | 稳定的 |
| 适用场景 | 数据量小切数组接近有序最佳 |
希尔排序(缩小增量的排序)
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing lncrementSort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell 于 1959年提出而得名。
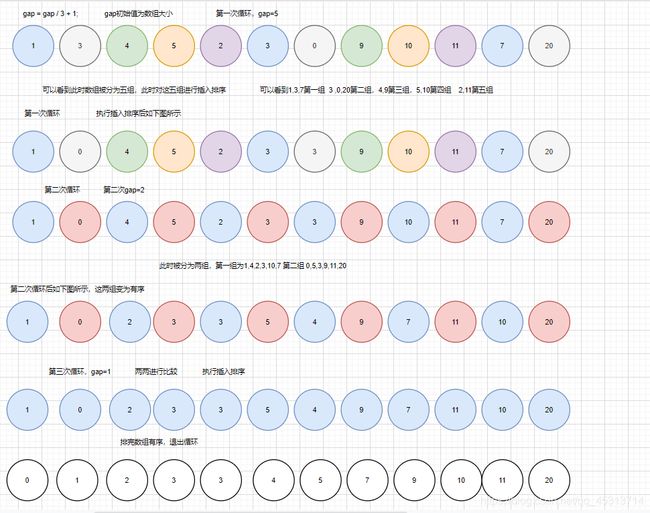
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
动画演示:
void shell_sort(int arr[],int len)
{
int key,i,j;
int gap = len;
while (gap > 1)
{
gap = gap / 3 + 1;
for ( i = gap; i < len; i++)
{
key = arr[i];//在一次循环中对多组进行操作
for ( j = i; j >= gap && key < arr[j - gap]; j -= gap)
{
arr[j] = arr[j - gap];
}
arr[j] = key;
}
}
}
| 希尔排序 | 对应的解 |
|---|---|
| 时间复杂度 | O(N^1.3)-O(N*N),跟gap取值有关,没有一个准确的值 |
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
| 适用场景 | 数据比较杂乱,适用于大型数组 |
堆排
动画演示:
堆排建堆:
因为我们此时要求的降序,所以建小堆
void adjust_down(int arr[], int n,int root)
{
int child = root * 2 + 1;
while (child < n)
{
if (child + 1 < n && arr[child + 1] < arr[child])
{
child += 1;
}
if (arr[child] < arr[root])
{
swap(&arr[child], &arr[root]);
root = child;
child = root * 2 + 1;
}
else
{
return;
}
}
}
思想:先求取它第一个非叶子结点,然后依次向下调整
for (int root = (len - 2) / 2; root >= 0; root--)
{
adjust_down(arr, len, root);
}
堆排代码:
利用删除思想,每次将堆顶元素置换到该堆的最后一个元素,同时再次执行向下调整,这样下次取出来的堆顶仍是当前堆的最小值
int end = len - 1;
while (end)
{
swap(&arr[end], &arr[0]);
adjust_down(arr, end, 0);
end--;
}
感觉这样呈现有点不清楚,还是把整个代码粘出来吧
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
void print(int arr[], int len)
{
for (int i = 0; i < len; i++)
{
printf("%3d", arr[i]);
}
printf("\n");
}
void adjust_down(int arr[], int n,int root)
{
int child = root * 2 + 1;
while (child < n)
{
if (child + 1 < n && arr[child + 1] < arr[child])
{
child += 1;
}
if (arr[child] < arr[root])
{
swap(&arr[child], &arr[root]);
root = child;
child = root * 2 + 1;
}
else
{
return;
}
}
}
void test01()
{
int arr[] = {
1,3,4,5,2,3,0,9,10 ,11, 7,20 };
int len = sizeof(arr) / sizeof(arr[0]);
for (int root = (len - 2) / 2; root >= 0; root--)
{
adjust_down(arr, len, root);
}
int end = len - 1;
while (end)
{
swap(&arr[end], &arr[0]);
adjust_down(arr, end, 0);
end--;
}
print(arr, len);
}
接下来分析一下时间复杂度:复杂度分为建堆的时间的复杂度+堆排的复杂度。

堆排时重新调整的复杂度,此时要循环n-1次,每次需要将堆顶元素向下调整log(n)步,所以堆排时重新调整的时间复杂度为O((n-1)log(n))≈O(nlogn)
总的时间复杂度等于建堆复杂度+堆排复杂度
O(n)=O(nlogn)+O(n)此时根据时间复杂度计算方法,舍弃掉较小的阶项
所以此时时间复杂度可以≈O(nlogn);
| 堆排序 | 对应的解 |
|---|---|
| 时间复杂度 | O(N*log(N) |
| 空间复杂度 | O(1) |
| 稳定性 | 不稳定 |
| 适用场景 | 适用于内存空间较少的情况,不能全部加载入内存,比如经典的top-K问题 |
基数排序
基数排序概念:基数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
动画演示
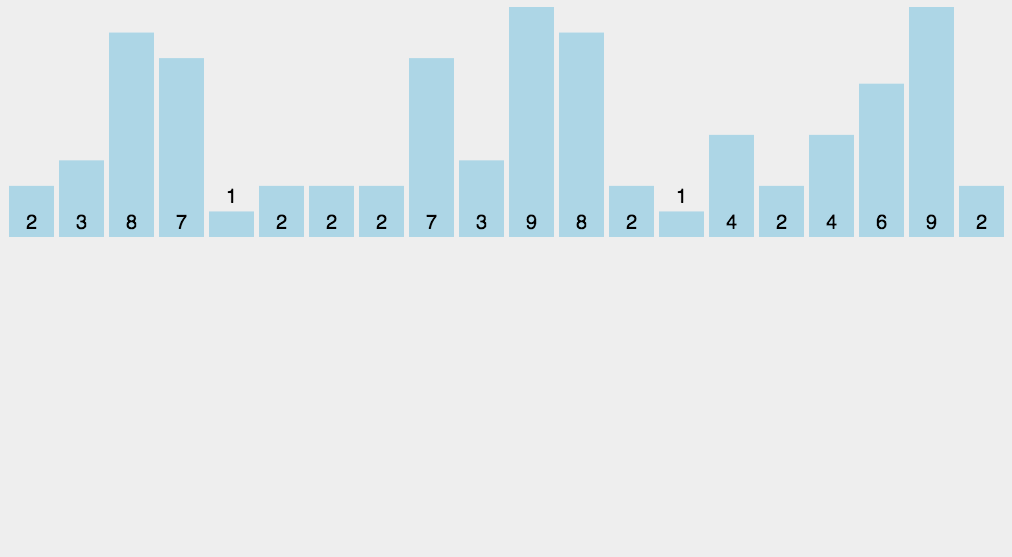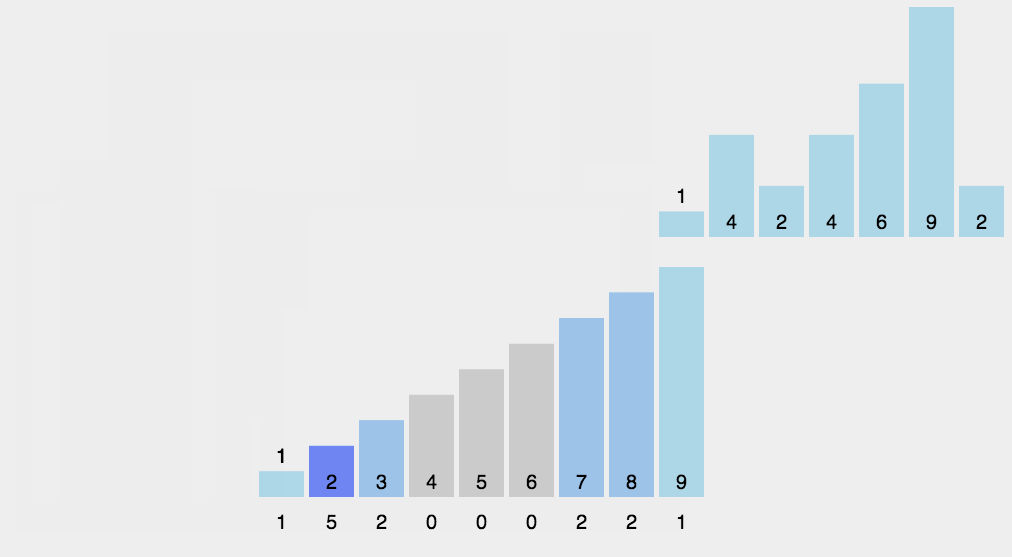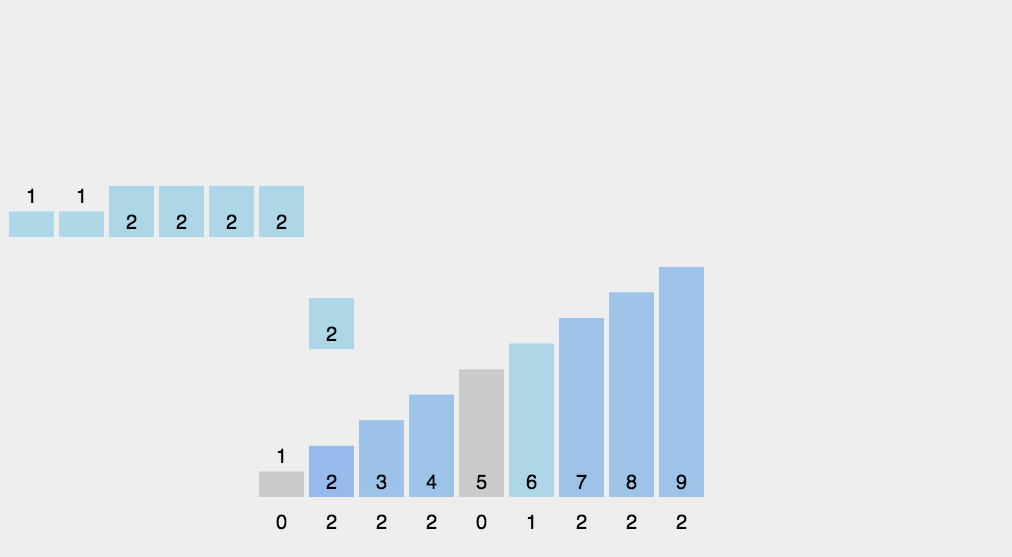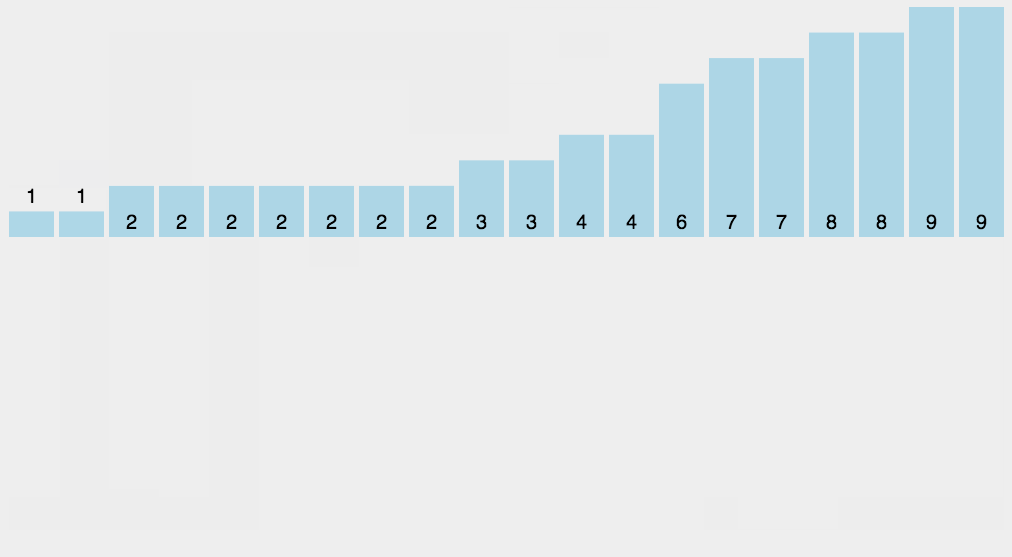
void cal_sort(int arr[],int size,int temp[])
{
for (int i = 0; i < len; i++)
{
temp[arr[i]]++;
}
}
void test()
{
int arr[] = {
1,2,3,1,2,3,4,1,2,3,4,8,5,6,7,9,10 };
int len = sizeof(arr) / sizeof(arr[0]);
int Max, Min;
Max = Min = 0;
for (int i = 1; i < len; i++)
{
if (arr[Max] < arr[i])
{
Max = i;
}
if (arr[Min] > arr[i])
{
Min = i;
}
}
int size = arr[Max] - arr[Min] + 1;//确定辅助空间大小
int* auxiliary_arr = (int*)calloc(sizeof(int) ,size);
//开辟辅助空间,将其初始值置为0;
if(auxiliary_arr==NULL)
{
return;
}
cal_sort(arr,len,auxiliary_arr);
//数组的复制,按区间每个元素每个元素重新赋值
int j=0;
for (int i = 0; i < size; i++)
{
int k = auxiliary_arr[i];//元素个数
while (k--)
{
arr[j++] = i;
}
}
//free()掉该部分空间
free(auxiliary_arr);
}
假设该部分区间的值集中在[m,n]中
| 计数排序 | 对应的解 |
|---|---|
| 时间复杂度 | O(N)N为元素个数 |
| 空间复杂度 | O(m-n+1) |
| 稳定性 | 稳定 |
| 适用场景 | 适用于数组中数值区间确定的,且数值范围不是很大的数组。不能是1到10000,那这样就得不偿失了。 |
同时,因为涉及到开辟额外空间,所以必须要释放掉该部分空间。
快排
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
从数列中挑出一个元素,称为 基准值。
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
快排动画演示图:
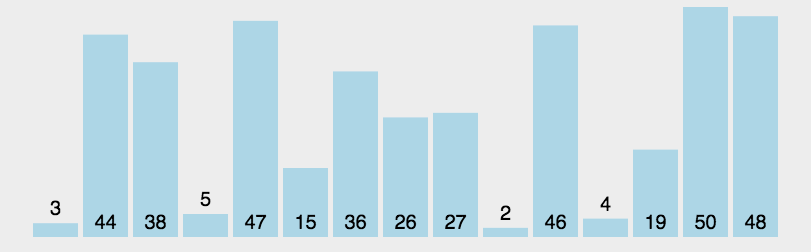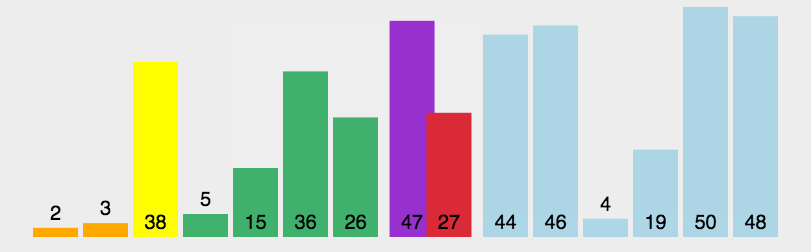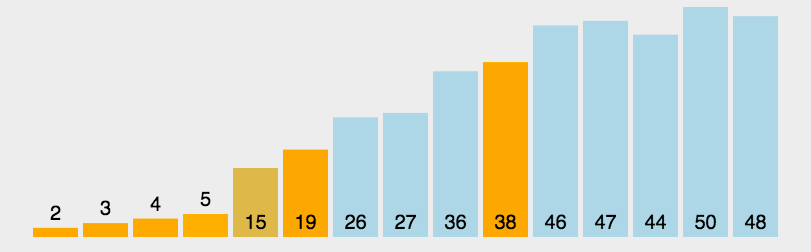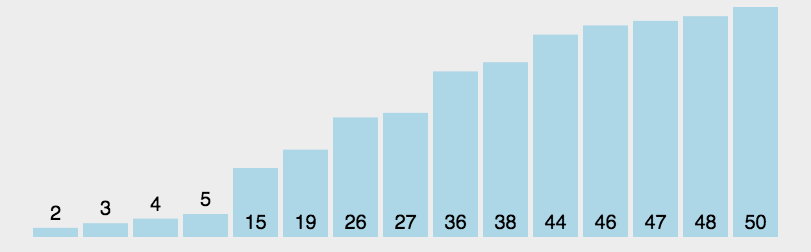
快排的递归做法
递归做法----hoare方法
算法思想:
1、找一个基准值key(一般三数取中法),本题中基准值为数组中最右的元素,再定义两个指针begin(指向首元素)和end(指向尾元素)
2、begin从前往后走找比基准值key大的元素(找到后停下),end从后往前走找比基准值小的元素(找到后也停下),
然后,交换array[begin]和array[end],依次循环操作。
3、当begin与end相遇,将array[begin]或array[end]与基准值交换。

交换值的函数,后面的swap均为该swap
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
int part(int arr[], int left, int right)
{
//将数组区间的最后一个元素作为它的基准值
int key = arr[right-1];
int begin = left;
int end = right - 1;
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
swap(&arr[begin], &arr[end]);
}
}
//交换基准值
if (begin != right - 1)
{
swap(&arr[begin], &arr[right - 1]);
}
return begin;
}
void Quick_sort(int arr[], int left, int right)
{
int div = 0;
if (right - left <1)
{
return;
}
div = part(arr, left, right);
//排左侧
Quick_sort(arr, left, div);
//排右侧
Quick_sort(arr, div + 1, right);
}
递归做法------挖坑法
1、定义begin和end分别指向数据的第一个元素和最后一个元素,基准值key为数组最后一个元素,array[end]元素的位置为一个坑
2、begin从前往后走,找比key大的值,找到之后,将array[begin]赋值给array[end],填充end位置的坑,此时begin位置为一个坑
3、end从后往前走,找比key小的值,找到之后,将array[end]赋值给array[begin],填充begin位置的坑,此时end位置为一个新的坑
4、此类方法依次填坑,当begin和end相遇,则循环结束,将key的值填最后一个坑。
//奈何博主的英语水平实在太垃圾,所以。。。
int wakeng(int arr[], int left, int right)
{
int begin = left;
int end = right - 1;
//记录一下该基准值
int key = arr[right - 1];
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
if (begin < end)
{
arr[end] = arr[begin];
end--;
}
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
arr[begin] = arr[end];
begin++;
}
}
//填最后一个坑
arr[begin] = key;
return begin;
}
void Quick_sort(int arr[], int left, int right)
{
int div = 0;
if (right - left < 1)
{
return;
}
div = wakeng(arr, left, right);
//排左侧
Quick_sort(arr, left, div);
//排右侧
Quick_sort(arr, div + 1, right);
}
递归做法-----快慢指针方法
算法思想:
1、选择一个基准值key,定义两个指针pre和cur(pre指向cur的前一个位置),pre和cur同时走,
当cur标记的元素比key大时,只有cur继续向前走(此时pre停下来),当cur走到标记的元素比pre小时,cur停下,此时交换array[cur]和array[pre+1],然后,pre往前走一步,cur继续往前走。
2、当cur走出界了,则将pre+1位置的值与key交换。

int part2(int arr[], int left, int right)
{
int cur = left;
int prev = cur - 1;
int key = arr[right - 1];
while (cur < right)
{
if (arr[cur] > key && ++prev != cur)
{
swap(&arr[cur], &arr[prev]);
}
cur++;
}
if (++prev != right - 1)
{
swap(&arr[prev], &arr[right - 1]);
}
return prev;
}
void Quick_sort(int arr[], int left, int right)
{
int div = 0;
if (right - left <1)
{
return;
}
div = part2(arr, left, right);
//排左侧
Quick_sort(arr, left, div);
//排右侧
Quick_sort(arr, div + 1, right);
}
快排非递归写法
既然可以使用递归方法,那我们此时也可以采用非递归的那种写法,原理就是将每次划分的区间依次入栈,再采取出栈的方式对该部分区间进行划分,同样也可以得到排序的方法,这里需要我们首先构建出栈这个空间
栈的定义:
typedef int datatype1;
typedef struct Stack {
datatype1 *val;
int size;
int capacity;
}Stack;
栈的初始化
void init1(Stack* s)
{
assert(s);
s->val = (datatype1*)malloc(sizeof(datatype1) * 5);
s->capacity = 5;
s->size = 0;
}
栈的扩容
void extend(Stack* s)
{
if (s->size == s->capacity)
{
s->val = (datatype1 *)realloc(s->val,sizeof(datatype1)* s->capacity * 2);
if (s->val == NULL)
{
printf("内存扩容失败\n");
return;
}
s->capacity *= 2;
}
}
入栈操作
void pushStack(Stack* s, datatype1 val)
{
assert(s);
extend(s);
s->val[s->size++] = val;
}
判断栈是否为空
bool is_empty(Stack* s)
{
assert(s);
if (s->size != 0)
{
return false;
}
return true;
}
出栈操作
void popStack(Stack* s)
{
if (is_empty(s))
{
return;
}
else
{
s->size--;
}
}
返回栈顶元素
datatype1 return_top(Stack* s)
{
if (is_empty(s))
{
return;
}
else
{
return s->val[s->size - 1];
}
}
栈的销毁
void destory1(Stack* s)
{
assert(s);
if (s->val != NULL)
{
free(s->val);
s->val = NULL;
}
}
快排非递归方法—hoare方法。
int part(int arr[], int left, int right)
{
//将数组的最后一个元素作为它的基准值
int key = arr[right - 1];
int begin = left;
int end = right - 1;
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
swap(&arr[begin], &arr[end]);
}
}
//交换基准值
if (begin != right - 1)
{
swap(&arr[begin], &arr[right - 1]);
}
return begin;
}
void Quicksort(int arr[], int n)
{
Stack s;
init1(&s);
int left = 0;
int right = n;
//首先将它的整体区间入栈[0,n)因为栈特性时先进后出,所以先入右区间,再入左区间
pushStack(&s, right);
pushStack(&s, left);
while (!is_empty(&s))
{
left = return_top(&s);
popStack(&s);
right = return_top(&s);
popStack(&s);
if (right - left > 1)
{
int div = part(arr, left, right);
//将划分好的右区间入栈
pushStack(&s, right);
pushStack(&s, div + 1);
//将划分好的左区间入栈
pushStack(&s, div);
pushStack(&s, left);
}
}
destory1(&s);
}
快排非递归方法—挖坑法
int wakeng(int arr[], int left, int right)
{
int begin = left;
int end = right - 1;
//记录一下该基准值
int key = arr[right - 1];
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
if (begin < end)
{
arr[end] = arr[begin];
end--;
}
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
arr[begin] = arr[end];
begin++;
}
}
//填最后一个坑
arr[begin] = key;
return begin;
}
void Quicksort(int arr[], int n)
{
Stack s;
init1(&s);
int left = 0;
int right = n;
//首先将它的整体区间入栈[0,n)因为栈特性时先进后出,所以先入右区间,再入左区间
pushStack(&s, right);
pushStack(&s, left);
while (!is_empty(&s))
{
left = return_top(&s);
popStack(&s);
right = return_top(&s);
popStack(&s);
if (right - left > 1)
{
int div = wakeng(arr, left, right);
//将划分好的右区间入栈
pushStack(&s, right);
pushStack(&s, div + 1);
//将划分好的左区间入栈
pushStack(&s, div);
pushStack(&s, left);
}
}
destory1(&s);
}
快排非递归–快慢指针做法
int part2(int arr[], int left, int right)
{
int cur = left;
int prev = cur - 1;
int key = arr[right - 1];
while (cur < right)
{
if (arr[cur] > key && ++prev != cur)
{
swap(&arr[cur], &arr[prev]);
}
cur++;
}
if (++prev != right - 1)
{
swap(&arr[prev], &arr[right - 1]);
}
return prev;
}
void Quicksort(int arr[], int n)
{
Stack s;
init1(&s);
int left = 0;
int right = n;
pushStack(&s, right);
pushStack(&s, left);
while (!is_empty(&s))
{
left = return_top(&s);
popStack(&s);
right = return_top(&s);
popStack(&s);
if (right - left > 1)
{
int div = part2(arr, left, right);
pushStack(&s, right);
pushStack(&s, div + 1);
pushStack(&s, div);
pushStack(&s, left);
}
}
destory1(&s);
}
快排的优化
每次基准值的选取都是很重要的,基准值选取的不同,会造成很多差异,比如,假设自己运气很背,每次选取值的时候都选择了最大/最小的那一个,此时应该怎么办?

就像上图这样,那应该怎么办?
这里给出一个方法:便是取中间值法(是接近中间值,并不一定是),最本质作用是可以最大化的避免极值作为基准值的情况。
取中间值法
原理:获取区间的左值和右值和中间值,选取出他们的三个的中间值作为基准值。
int getMId(int arr[], int left, int right)
{
int mid = left + ((right - left) >> 1);
if (arr[left] < arr[right - 1])
{
if (arr[mid] < arr[left])
return left;
else
{
if (arr[mid] > arr[right - 1])
return right - 1;
else
return mid;
}
}
else
{
if (arr[mid] > arr[left])
return left;
else
{
if (arr[mid] < arr[right - 1])
return right - 1;
else
return mid;
}
}
}
这时候我们用hoare法做一个示范,后面两个方法同理
int part(int arr[], int left, int right)
{
//将数组的最后一个元素作为它的基准值
int mid = getMId(arr, left, right);
swap(&arr[mid], &arr[right - 1]);//为了保持后面的语句不改变,先将基准值交换到right-1的位置。
int key = arr[right - 1];
int begin = left;
int end = right - 1;
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
swap(&arr[begin], &arr[end]);
}
}
//交换基准值
if (begin != right - 1)
{
swap(&arr[begin], &arr[right - 1]);
}
return begin;
}
利用插入排序来优化快排
众所周知,插入排序在处理数据量小和接近有序数组的时候其效率是最好的,因为非递归还好,若采用递归的方式,如果数据量过大的话难免会造成栈的溢出。我们可以通过设置阈值,当right’-left<某一特定值时,采用插入排序,不让他一直递归下去。
这里还是非递归方式,递归方式同理:
这里给个完成代码把!
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
void print(int arr[], int len)
{
for (int i = 0; i < len; i++)
{
printf("%3d", arr[i]);
}
printf("\n");
}
int getMId(int arr[], int left, int right)
{
int mid = left + ((right - left) >> 1);
if (arr[left] < arr[right - 1])
{
if (arr[mid] < arr[left])
return left;
else
{
if (arr[mid] > arr[right - 1])
return right - 1;
else
return mid;
}
}
else
{
if (arr[mid] > arr[left])
return left;
else
{
if (arr[mid] < arr[right - 1])
return right - 1;
else
return mid;
}
}
}
int wakeng(int arr[], int left, int right)
{
int begin = left;
int end = right - 1;
//记录一下该基准值
int mid = getMId(arr, left, right);
swap(&arr[mid], &arr[right - 1]);
int key = arr[right - 1];
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
if (begin < end)
{
arr[end] = arr[begin];
end--;
}
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
arr[begin] = arr[end];
begin++;
}
}
//填最后一个坑
arr[begin] = key;
return begin;
}
int part2(int arr[], int left, int right)
{
int cur = left;
int prev = cur - 1;
int mid = getMId(arr, left, right);
swap(&arr[mid], &arr[right - 1]);
int key = arr[right - 1];
while (cur < right)
{
if (arr[cur] > key && ++prev != cur)
{
swap(&arr[cur], &arr[prev]);
}
cur++;
}
if (++prev != right - 1)
{
swap(&arr[prev], &arr[right - 1]);
}
return prev;
}
int part(int arr[], int left, int right)
{
//将数组的最后一个元素作为它的基准值
int mid = getMId(arr, left, right);
swap(&arr[mid], &arr[right - 1]);
int key = arr[right - 1];
int begin = left;
int end = right - 1;
while (begin < end)
{
while (begin < end && arr[begin] >= key)
begin++;
while (begin < end && arr[end] <= key)
end--;
if (begin < end)
{
swap(&arr[begin], &arr[end]);
}
}
//交换基准值
if (begin != right - 1)
{
swap(&arr[begin], &arr[right - 1]);
}
return begin;
}
void insert(int arr[], int left, int right)
{
for (int i = left + 1; i < right; i++)
{
if (arr[i] > arr[i - 1])
{
int j = i - 1;
int temp = arr[i];
while (j >= 0 && temp > arr[j])
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = temp;
}
}
}
void Quicksort(int arr[], int n)
{
Stack s;
init1(&s);
int left = 0;
int right = n;
pushStack(&s, right);
pushStack(&s, left);
while (!is_empty(&s))
{
left = return_top(&s);
popStack(&s);
right = return_top(&s);
popStack(&s);
//此处便是我设立的阈值,当区间内元素小于5的时候,采用插入来优化该算法。
if (right - left > 5)
{
int div = wakeng(arr, left, right);
pushStack(&s, right);
pushStack(&s, div + 1);
pushStack(&s, div);
pushStack(&s, left);
}
else
{
insert(arr, left, right);
}
}
destory1(&s);
}
快排的时间复杂度与空间复杂度及应用场景
| 快排 | 相关的解 |
|---|---|
| 时间复杂度 | O(N*logN) 极端情况下为O(N^2),就是每次基准值都选在了极值上 |
| 空间复杂度 | O(logN)表示的是递归的层数,假如它为完全二叉树情况下。极端情况下为单支树的情况,O(N)。在非递归下为O(1)因为不会有递归带来的栈消耗 |
| 稳定性 | 不稳定 |
| 应用场景 | 适用于数据量较大且分布较为杂乱的情况,这种情况下用快排和结合插入排序使用是比较好的,快排可以将区间中元素处理到较为有序,此时采用插入排序来进行局部排序。 |
归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
动画展示


递归下的归并算法
核心思想:先对整个区间的元素进行划分,直至划分到元素个数为1时停止划分,然后两两开始依据大小值进行归并。
合并算法
void merge(int arr[], int temp[], int left, int mid, int right)
{
//标记左半区的
int l_pos = left;
//标记右边的
int r_pos = mid;
//记录temp数组下标
int pos = left;
while (l_pos < mid && r_pos < right)
{
if (arr[l_pos] > arr[r_pos])
{
temp[pos++] = arr[l_pos++];
}
else
{
temp[pos++] = arr[r_pos++];
}
}
while (r_pos < right)
{
temp[pos++] = arr[r_pos++];
}
while (l_pos < mid )
{
temp[pos++] = arr[l_pos++];
}
//将归并好的区间值重新赋值回原数组
while (left < right)
{
arr[left] = temp[left];
left++;
}
}
划分算法
void msort(int arr[], int temp[], int left, int right)
{
//当它划分到只有一个元素的时候,此时停止划分
if (right - left <= 1)
{
return;
}
if (left < right)
{
//找中间点
int mid = (left + right) / 2;
//递归划分左边的
msort(arr, temp, left, mid);//区间都是左闭右开的区间[left,mid)
//递归划分右边的
msort(arr, temp, mid , right);//[mid,right)
//对划分的区间进行合并
merge(arr, temp, left, mid, right);
}
}
调用函数
void mergesort(int arr[],int len,int temp[])
{
msort(arr, temp, 0, len );
}
void test01()
{
int arr[] = {
1,3,4,5,2,3,0,9,10 ,11, 7,20 };
int len = sizeof(arr) / sizeof(arr[0]);
int* temp = (int*)malloc(sizeof(int) * len);
mergesort(arr, len,temp);
/*print(temp, 13);*/
free(temp);//开辟的空间是要释放的,此时在调用完后释放它
print(arr, len);
}
非递归下的归并算法
算法思想:既然递归归并是先划分为一个一个的小区间进行操作的,那我们此时为什么不能从小区间开始到大区间(整个数组)直接进行划分呢?下面便是我给出的方法。
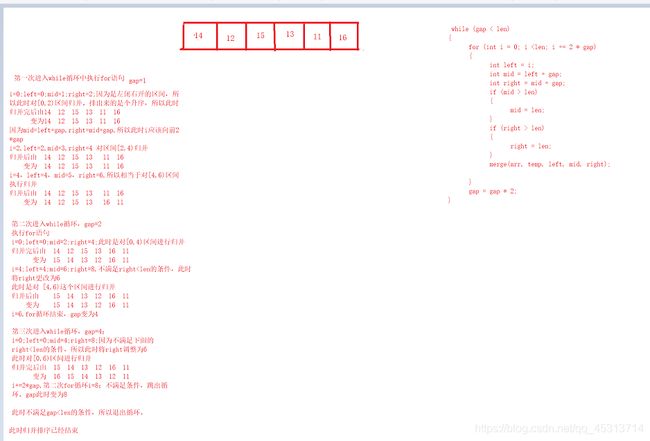
归并算法
void merge(int arr[], int temp[], int left, int mid, int right)
{
//标记左半区的
int l_pos = left;
//标记右边的
int r_pos = mid;
//记录temp数组下标
int pos = left;
while (l_pos < mid && r_pos < right)
{
if (arr[l_pos] > arr[r_pos])
{
temp[pos++] = arr[l_pos++];
}
else
{
temp[pos++] = arr[r_pos++];
}
}
while (r_pos < right)
{
temp[pos++] = arr[r_pos++];
}
while (l_pos < mid)
{
temp[pos++] = arr[l_pos++];
}
while (left < right)
{
arr[left] = temp[left];
left++;
}
}
//划分算法
void merge_sortno(int arr[], int temp[], int len)
{
int gap = 1;
while (gap < len)
{
for (int i = 0; i <len; i += 2 * gap)
{
int left = i;
int mid = left + gap;
int right = mid + gap;
if (mid > len)
{
mid = len;
}
if (right > len)
{
right = len;
}
merge(arr, temp, left, mid, right);
}
gap = gap * 2;
}
}
算法调用
void test01()
{
int arr[] = {
1,3,4,5,2,3,0,9,10 ,11, 7,20 };
int len = sizeof(arr) / sizeof(arr[0]);
int* temp = (int*)malloc(sizeof(int) * len);
merge_sortno(arr, temp, len);
free(temp);
print(arr, len);
}
| 归并排序 | 相应的解 |
|---|---|
| 时间复杂度 | 因为归并排序每次都是进行一分为二的操作,就可以把它视为一个完全二叉树,每层有n个元素,共有logn层,所以时间复杂度为O(nlogn) |
| 空间复杂度 | O(n) |
| 稳定性 | 稳定 |
| 适用场合 | 数组数据量较少,分布杂乱的情况 |
归并排序与快速排序(快排)对比
快排的优点:不需要借助辅助空间,在基准值选的较好的情况下可以达到时间复杂度为O(nlogn)的效果。
快排缺点:基准值若选的不好的话,此时划分出来的树为单支树,其时间复杂度退化为O(n^2);
归并排序优点:每次划分不用理睬基准值,都是一分为2的,所以它的时间度在最差与最好情况下皆为O(nlogn)
归并排序的缺点:需要借助辅助空间,类似于空间换时间的操作,所以在内部排序中,很少会采用归并排序,而是转去采用快速排序。因为归并排序会造成很大的内存消耗。得不偿失。
巧记八大排序中各个算法稳定性
快(快排)些(希尔排序)选(选择排序)一堆(堆排序)美女。。这是不稳定的
这样剩下的插入排序,归并排序,冒泡排序,基数排序便是稳定的。