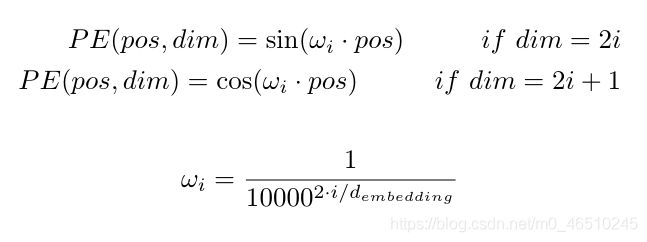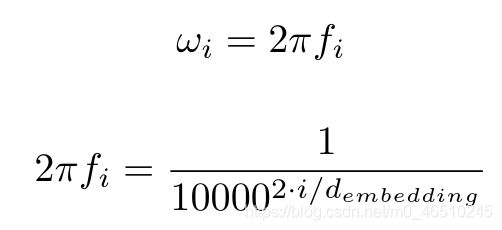位置编码在注意力机制中的作用

阅读本文的前置知识

• 神经网络知识。
• 有一种叫做注意机制的东西，但是你不需要知道注意力具体实现。
• RNN/LSTM的不足。

A. Vaswani等人的《Attention Is All You Need》被认为是解决了众所周知的LSTM/RNN体系结构在深度学习空间中的局限性的突破之一。本文介绍了transformers 在seq2seq任务中的应用。 该论文巧妙地利用了 D.Bahdanau 等人通过联合学习对齐和翻译的神经机器翻译注意机制的使用。 并且提供一些示例明确且详尽地解释了注意力机制的数学和应用。

在本文中，我将专注于注意力机制的位置编码部分及其数学。

假设您正在构建一个 seq2seq 学习任务，并且您想要开发一个模型，该模型将输入英语句子并将其翻译成其他 语言。
"All animals are equal but some are more equal than others "→Badhā prāṇī’ō samāna chē parantu kēṭalāka an’ya karatā vadhu samāna chē
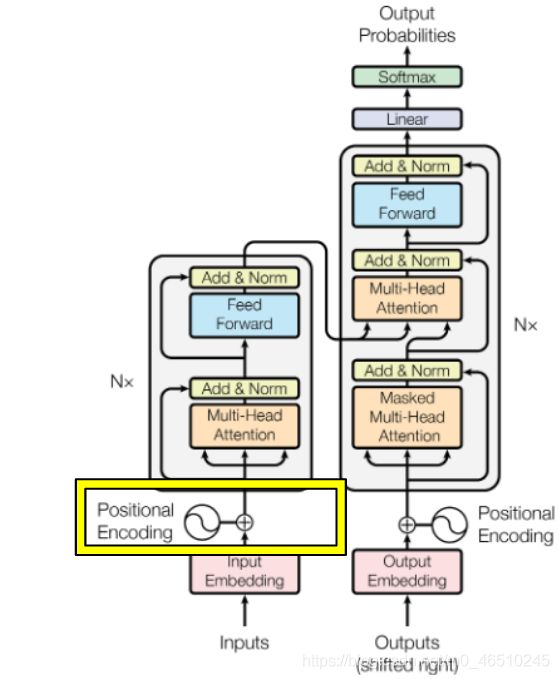
你的第一步是获取这个输入句子，运行一个分词器，将它转换成数字，然后将它传递给一个嵌入层，这可能会为这个句子中的每个单词添加一个额外的维度。在运行 RNN 或 LSTM 时，隐藏状态保留单词在句子中的相对位置信息。然而，在 Transformer 网络中，如果编码器包含一个前馈网络，那么只传递词嵌入就等于为您的模型增加了不必要的混乱，因为在词嵌入中没有捕获有关句子的顺序信息。为了处理单词相对位置的问题，位置编码的想法出现了。

在从嵌入层提取词嵌入后，位置编码被添加到这个嵌入向量中。

解释位置编码最简单的方法是为每个单词分配一个唯一的数字 ∈ ℕ 。或者为每个单词分配一个在 [0,1] ∈ ℝ 范围内的实数（如果输入句子很长，这样可以处理很大的值）。但是，上述两种方法都没有捕捉到单词之间时间步长的准确性。为了克服这个问题，本文使用了 sin 和 cosine 函数形式的位置编码。

打个比方，我们输入模型的序列，无论是句子、视频序列还是股票市场价格数据，都将始终是时域信号。表示时域信号的最佳方式是通过正弦方程 sin(ωt)。如果我们巧妙地使用这个波动方程，我们可以在一次拍摄中捕获词嵌入的时间和维度信息。

让我们看一下这个等式，在接下来的步骤中，我们将尝试把它形象化。

让我们考虑一个简单的句子，它被分词，然后它的词嵌入被提取。句子长度为5，嵌入维数为8。因此，每个单词都表示为1x8的向量。

现在我们在时间维度上取一个序列把正弦PE向量加到这个嵌入向量上。

进一步，我们对沿dim维数的其他向量做类似的操作。

本文在嵌入向量中交替加入正弦和余弦。如果dim是偶数，则sin级数相加，如果dim是奇数，则cos级数相加。

这很好地捕获了沿时间维度（或等式中描述的 pos 维度。我将 pos 和 time 互换使用，因为它们意味着相同的事情）但是如何也捕获沿dims维度的相对位置信息呢？ 这里的答案也在于等式本身。 ω 项。

随着 i 从 0 增加到 d_embedding/2，频率也从 1/2π 减少到 1/(2π.10000)

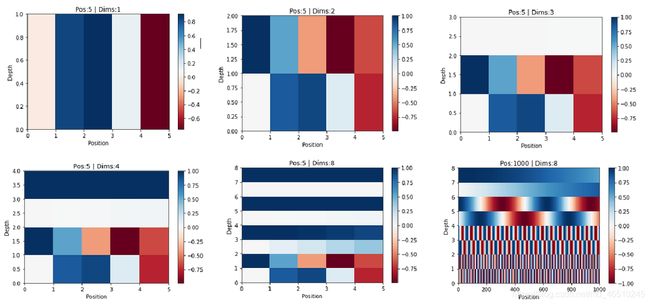
因此我们看到，沿着无序方向的每个向量，位置的唯一性被捕获。 该论文还描述了这种编码的鲁棒性。 但是我仍然无法找出为什么特别使用数字 10000 进行位置编码（它可能是一个超参数吗？）。 这个解释粗略地展示了如何使用正弦和余弦对于模型理解是非常合理和有效的。 下面的图表本身讲述了位置编码如何随位置（时间）和尺寸变化。

人们可以很容易地看到，这些是简单的时频图，其中位置代表时间，深度代表频率。 时间频率图已被用于从射电天文学到材料光谱分析的许多应用中。 因此，从现有的现实世界系统构建类比确实可以更好地理解问题。

这是我对注意力机制中使用的位置编码的看法。 在接下来的系列中，我将尝试撰写有关编码器-解码器部分的内容，并将注意力应用于现实世界的规模问题。

的看法。 在接下来的系列中，我将尝试撰写有关编码器-解码器部分的内容，并将注意力应用于现实世界的规模问题。