前言
在上一篇文章中,我们了解了k近邻算法,也学习了KNN算法的流程,并且手动实现了python代码和封装。
那么在得到了分类的结果之后,它的效果如何呢?预测的准不准确?
这里我们学习一些评估分类问题常用的指标
判断模型好坏
训练数据集和测试数据集
当我们训练好一个模型之后,一般是不能直接拿到生产环境中直接使用的,我们首先要考虑和评估这个模型准确度如何。但是拿到真实环境中,数据是没有标签的,我们没有办法验证,那么该这么办呢?
既然是这样,那么我们可以将原始数据中的一部分作为训练数据,另一部分作为测试数据,训练好模型之后,使用测试数据进行验证模型的好坏。
那么如何对原始数据进行拆分呢?
有时候我们的数据可能是直接排序好的,这样的话,直接拆分可能会导致测试数据的类型标签形成了一定的规律,所以我们先对数据进行一个shuffle操作把数据打乱。
如果数据集的特征和标签是在一起的,那么可以直接shuffle之后再分解成特征和标签。
如果特征和标签不在一起,可以使用下面的两种方法解决这一问题:
1、将X和y合并为同一个矩阵,然后对矩阵进行shuffle,之后再分解
2、对y的索引进行乱序,根据索引确定与X的对应关系,最后再通过乱序的索引进行赋值
(在后面的实现代码中会给出具体代码)
得到分割好的训练集和测试集之后,就可以应用到KNN算法中去。训练集传入fit函数中进行训练,然后对测试集的特征集进行预测,得到预测的标签集。再对预测的标签集和实际测试集的标签集进行对比。可以得到预测正确的比例。
指标1-分类准确度accuracy
到这里我们就可以引入第一个指标的概念:accuracy(分类准确度)。上面的预测的标签集中正确的比例就是分类的准确度
这里我们利用之前手写的KNN算法整体实现一下数据切分和训练得出分类准确度
使用得数据集是鸢尾花数据集,特征有4个,种类有三个标签。
代码实现:
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
import collections
#定义一个将多维数据转为一维数据的函数
def flatten(x):
result = []
for el in x:
if isinstance(x, collections.Iterable) and not isinstance(el, str) and not isinstance(el, float):
result.extend(flatten(el))
else:
result.append(el)
return result
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 切分训练集和测试集方法1
# 使用concatenate函数进行拼接,因为传入的矩阵必须具有相同的形状。
#因此需要对label进行reshape操作,reshape(-1,1)表示行数自动计算,1列。axis=1表示纵向拼接。
tempConcat = np.concatenate((X, y.reshape(-1,1)), axis=1)
# 拼接好后,直接进行乱序操作
np.random.shuffle(tempConcat)
# 再将shuffle后的数组使用split方法拆分
shuffle_X,shuffle_y = np.split(tempConcat, [4], axis=1)
# 设置划分的比例
test_ratio = 0.2
test_size = int(len(X) * test_ratio)
X_train = shuffle_X[test_size:]
y_train = shuffle_y[test_size:]
X_test = shuffle_X[:test_size]
y_test = shuffle_y[:test_size]
#转化方法1 这里需要降维转化是因为我们手写的knn算法中需要这种数据格式 下面转化2方法也是同理。
y_train = flatten(y_train)
y_train = np.array(y_train)
#转化2
# y_train = y_train.tolist()
# y_train1=[]
# for y_ in y_train:
# y_train1.append(y_[0])
# y_train1= np.array(y_train1)
# print(y_train1)
# # 切分训练集和测试集方法2
# # 将x长度这么多的数,返回一个新的打乱顺序的数组,
# #注意,数组中的元素不是原来的数据,而是混乱的索引
# shuffle_index = np.random.permutation(len(X))
# # 指定测试数据的比例
# test_ratio = 0.2
# test_size = int(len(X) * test_ratio)
# test_index = shuffle_index[:test_size]
# train_index = shuffle_index[test_size:]
# X_train = X[train_index]
# X_test = X[test_index]
# y_train = y[train_index]
# y_test = y[test_index]
# print(y_train)
%run myKnn/kNN.py
#from myKnn.kNN import kNNClassifier
knn_clf = kNNClassifier(k=3)
knn_clf.fit(X_train, y_train)
y_predict = knn_clf.predict(X_test)
print(y_predict)
print(np.array(flatten(y_test)))
# 两个向量的比较,返回一个布尔型向量,对这个布尔向量(faluse=1,true=0)sum,
true_sum=sum(y_predict ==np.array(flatten(y_test)))
accuracy=true_sum/len(y_test)
accuracy
结果:
[0. 2. 0. 1. 0. 1. 0. 2. 0. 1. 1. 1. 1. 2. 2. 1. 2. 1. 0. 2. 2. 0. 2. 2.
0. 2. 0. 1. 2. 0.]
[0. 2. 0. 1. 0. 1. 0. 2. 0. 1. 1. 1. 1. 2. 2. 1. 2. 1. 0. 2. 2. 0. 2. 1.
0. 2. 0. 1. 2. 0.]
0.9666666666666667
accuracy指标定义清洗、计算方法简单,因此经常被使用。但是只使用accuracy评价分类算法,是有很大问题的。
比如,对于一个癌症预测系统,,输入检查指标,判断是否患有癌症,预测准确度99.9%,那这个系统是好还是坏呢?
很显然,如果癌症的发生率是0.1%,那其实不使用任何机器学习算法,只要系统预测所有人都健康,就可以达到99.9%的准确度,也就是说对于极度偏斜(Skewed Data)的数据,只使用分类准确度是不能衡量的。
这就需要使用混淆矩阵(Confusion Matrix)做进一步分析。
混淆矩阵
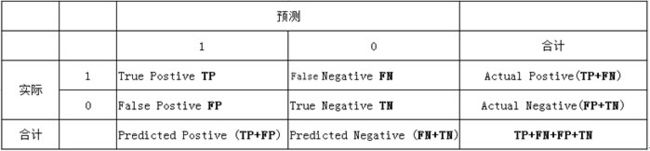
我们来看经典的混淆矩阵图
针对一个二分类问题,将实例分成正类(postive)或者负类(negative)。但是实际中分类时,会出现四种情况:
(1)真正类(True Positive , TP):被模型预测为正类的正样本
(2)假正类(False Positive , FP):被模型预测为正类的负样本
(3)假负类(False Negative , FN):被模型预测为负类的正样本
(4)真负类(True Negative , TN):被模型预测为负类的负样本
列联表如下,1代表正类,0代表负类:
现在假设有1万人进行预测,填入混淆矩阵如下:
对于1万个人中,有9978个人本身并没有癌症,我们的算法也判断他没有癌症;有12个人本身没有癌症,但是我们的算法却错误地预测他有癌症;有2个人确实有癌症,但我们算法预测他没有癌症;有8个人确实有癌症,而且我们也预测对了。
因为混淆矩阵表达的信息比简单的分类准确度更全面,因此可以通过混淆矩阵得到一些有效的指标
指标2-精准率和召回率
根据混淆矩阵可以求得指标:
精准率:precision = TP/(TP+FP) ,即精准率为8/(8+12)=40%。所谓的精准率是:分母为所有预测为1的个数,分子是其中预测对了的个数,即预测值为1,且预测对了的比例。
为什么管它叫精准率呢?在有偏的数据中,我们通常更关注值为1的特征,比如“患病”,比如“有风险”。在100次结果为患病的预测,平均有40次预测是对的。即精准率为我们关注的那个事件,预测的有多准。
召回率:recall = TP/(TP+FN),即召回率为8/(8+2)=80%。所谓召回率是:所有真实值为1的数据中,预测对了的个数。每当有100个癌症患者,算法可以成功的预测出8个 。也就是我们关注的那个事件真实的发生情况下,我们成功预测的比例是多少。
那么为什么需要精准率和召回率呢?还是下面的这个例子,有10000个人,混淆矩阵如下:
如果我们粗暴的认为所有人都是健康的,那算法的准确率是99.78%,但这是毫无意义的。如果算精准率则是40%,召回率是80%。
更关注哪个呢?
精准率(查准率):预测值为1,且预测对了的比例,即:我们关注的那个事件,预测的有多准。
召回率(查全率):所有真实值为1的数据中,预测对了的个数,即:我们关注的那个事件真实的发生情况下,我们成功预测的比例是多少。
有时候,对于一个算法而言,精准率和召回率没有达到同时高或者低,这时候我们需要根据场景而定来取舍依赖的指标。
比如我们做了一个股票预测系统,未来股票是还是这样一个二分类问题。很显然“涨”才是我们关注的焦点,那么我们肯定希望:系统预测上涨的股票中,真正上涨的比例越大越好,这就是希望查准率高。那么我们是否关注查全率呢?在大盘中有太多的真实上涨股票,虽然我们漏掉了一些上升周期,但是我们没有买进,也就没有损失。但是如果查准率不高,预测上涨的结果下跌了,那就是实实在在的亏钱了。所以在这个场景中,查准率更重要。
当然也有追求召回率的场景,在医疗领域做疾病诊断,如果召回率低,意味着本来有一个病人得病了,但是没有正确预测出来,病情就恶化了。我们希望尽可能地将所有有病的患者都预测出来,而不是在看在预测有病的样例中有多准。
但是,在实际业务场景中,也有很多没有这么明显的选择。那么在同时需要关注精准率和召回率,如何在两个指标中取得平衡呢?在这种情况下,我们使用一种新的指标:F1 Score。
指标2-二者兼顾 F1 Score
如果要我们综合精准率和召回率这两个指标,我们可能会想到取平均值这样的方法。F1 Score的思想也差不多:
F1 Score 是精准率和召回率的调和平均值。
指标3-ROC曲线和AUC
在了解ROC曲线之前,先了解三个概念:分类阈值、TPR和FPR
分类阈值
分类阈值,即设置判断样本为正例的阈值thr
如果某个逻辑回归模型对某封电子邮件进行预测时返回的概率为 0.9995,则表示该模型预测这封邮件非常可能是垃圾邮件。相反,在同一个逻辑回归模型中预测分数为 0.0003 的另一封电子邮件很可能不是垃圾邮件。可如果某封电子邮件的预测分数为 0.6 呢?为了将逻辑回归值映射到二元类别,您必须指定分类阈值(也称为判定阈值)。如果值高于该阈值,则表示“垃圾邮件”;如果值低于该阈值,则表示“非垃圾邮件”。人们往往会认为分类阈值应始终为 0.5,但阈值取决于具体问题,因此您必须对其进行调整。
TPR和FPR
借助之前的图我们看一下:
TPR:预测为1,且预测对了的数量,占真实值为1的数据百分比。很好理解,就是召回率。
TPR = recall = TP/(TP+FN)
FPR:预测为1,但预测错了的数量,占真实值不为1的数据百分比。与TPR相对应,FPR除以真实值为0的这一行所有的数字和 。
ROC曲线
ROC曲线(Receiver Operation Characteristic Cureve),描述TPR和FPR之间的关系。x轴是FPR,y轴是TPR
假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如0.6,概率大于等于0.6的为正类,小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。
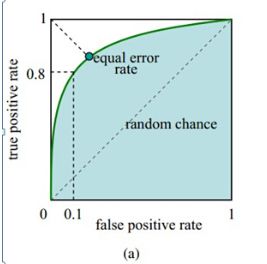
如下面这幅图,(a)图中实线为ROC曲线,线上每个点对应一个阈值。
我们已经知道, TPR就是所有正例中,有多少被正确地判定为正;FPR是所有负例中,有多少被错误地判定为正。 分类阈值取不同值,TPR和FPR的计算结果也不同,最理想情况下,我们希望所有正例 & 负例 都被成功预测 TPR=1,FPR=0,即 所有的正例预测值 > 所有的负例预测值,此时阈值取最小正例预测值与最大负例预测值之间的值即可。
TPR越大越好,FPR越小越好,但这两个指标通常是矛盾的。为了增大TPR,可以预测更多的样本为正例,与此同时也增加了更多负例被误判为正例的情况。
AUC
一般在ROC曲线中,我们关注是曲线下面的面积, 称为AUC(Area Under Curve)。这个AUC是横轴范围(0,1 ),纵轴是(0,1)所以总面积是小于1的。
ROC和AUC的主要应用:比较两个模型哪个好?主要通过AUC能够直观看出来。
ROC曲线下方由梯形组成,矩形可以看成特征的梯形。因此,AUC的面积可以这样算:(上底+下底)* 高 / 2,曲线下面的面积可以由多个梯形面积叠加得到。AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样,模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
以下示例三种AUC值(曲线下面积)
为什么我们使用ROC和AUC呢
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
总结
这一节我们了解了各种评价分类模型好坏的指标,具体使用哪一种,是依据应用场景而定
参考:https://blog.csdn.net/guohecang/article/details/52276548