Python小白的数学建模课-09 微分方程模型

小白往往听到微分方程就觉得害怕，其实数学建模中的微分方程模型不仅没那么复杂，而且很容易写出高水平的数模论文。

本文介绍微分方程模型的建模与求解，通过常微分方程、常微分方程组、高阶常微分方程 3个案例手把手教你搞定微分方程。

通过二阶 RLC 电路问题，学习微分方程模型的建模、求解和讨论。

欢迎关注『Python小白的数学建模课 @ Youcans』系列，每周持续更新

---

1. 微分方程

1.1 基本概念

微分方程是描述系统的状态随时间和空间演化的数学工具。物理中许多涉及变力的运动学、动力学问题，如空气的阻力为速度函数的落体运动等问题，很多可以用微分方程求解。微分方程在化学、工程学、经济学和人口统计等领域也有广泛应用。

具体来说，微分方程是指含有未知函数及其导数的关系式。

• 微分方程按自变量个数分为：只有一个自变量的常微分方程（Ordinary Differential Equations）和包含两个或两个以上独立变量的偏微分方程（Partial Differential Equations）。
• 微分方程按阶数分为：一阶、二阶、高阶，微分方程的阶数取决于方程中最高次导数的阶数。
• 微分方程还可以分为：（非）齐次，常（变）系数，（非）线性，初值问题/边界问题…

以上内容看看就算了，看多了就吓跑了。

欢迎关注 『Python小白的数学建模课 @ Youcans』 系列，持续更新
Python小白的数学建模课-A1.国赛赛题类型分析
Python小白的数学建模课-A2.2021年数维杯C题探讨
Python小白的数学建模课-A3.12个新冠疫情数模竞赛赛题及短评
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型

1.2 微分方程的数学建模

微分方程的数学建模其实并不复杂，基本过程就是分析题目属于哪一类问题、可以选择什么微分方程模型，然后如何使用现有的微分方程模型建模。

在数学、力学、物理、化学等各个学科领域的课程中，针对该学科的各种问题都会建立适当的数学模型。在中学课程中，各学科的数学模型主要是线性或非线性方程，而在大学物理和各专业的课程中，越来越多地出现用微分方程描述的数学模型。

数学建模中的微分方程问题，通常还是这些专业课程中相对简单的模型，专业课程的教材在介绍一个模型时，往往都做了非常详细的讲解。只要搞清楚问题的类型、选择好数学模型，建模和求解并不是很难，而且在撰写论文时对问题背景、使用范围、假设条件、求解过程有大量现成的内容可以复制参考。

小白之所以害怕，一是看到微分方程就心里发怵，二是缺乏专业背景，不知道从哪里查资料、不能判断问题的类型、不知道选择什么模型、不善于从题目内容得出模型参数，也不知道如何编程求解。所以，老师说，一看这就是××问题，显然就可以用××模型。小白说，我们还是换 B题吧。

本系列将会从简单的微分方程模型入手，重点介绍微分方程数值解法的编程实现，并通过分析问题、建立模型的案例帮助小白树立信心和动力。

希望你在学习本系列之后，会发现微分方程模型是数学建模中最容易的题型：模型找教材，建模找例题，求解有例程，讨论有套路，论文够档次。

1.3 微分方程的数值解法

在学习专业课程时，经常会推导和求解微分方程的解析解，小白对微分方程模型的恐惧就是从高等数学“微分方程”开始，经过专业课的不断强化而形成的。实际上，只有很少的微分方程可以解析求解，大多数的微分方程只能采用数值方法进行求解。

微分方程的数值求解是先把时间和空间离散化，然后将微分化为差分，建立递推关系，然后反复进行迭代计算，得到任意时间和空间的值。

如果你还是觉得头晕目眩，我们可以说的更简单一些。建模就是把专业课教材上的公式抄下来，求解就是把公式的参数输入到 Python 函数中。

我们先说求解。求解常微分方程的基本方法，有欧拉法、龙格库塔法等，可以详见各种教材，撰写数模竞赛论文时还是可以抄几段的。本文沿用“编程方案”的概念，不涉及这些算法的具体内容，只探讨如何使用 Python 的工具包、库函数，零基础求解微分方程模型。

我们的选择是 Python 常用工具包三剑客：Scipy、Numpy 和 Matplotlib：

• Scipy 是 Python 算法库和数学工具包，包括最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号和图像处理、常微分方程求解等模块。有人介绍 Scipy 就是 Python 语言的 Matlab，所以大部分数学建模问题都可以用它搞定。
• Numpy 提供了高维数组的实现与计算的功能，如线性代数运算、傅里叶变换及随机数生成，另外还提供了与 C/C++ 等语言的集成工具。
• Matplotlib 是可视化工具包，可以方便地绘制各种数据可视化图表，如折线图、散点图、直方图、条形图、箱形图、饼图、三维图，等等。

顺便说一句，还有一个 Python 符号运算工具包 SymPy，以解析方式求解积分、微分方程，也就是说给出的结果是微分方程的解析解表达式。很牛，但只能求解有解析解的微分方程，所以，你知道就可以了。

---

2. SciPy 求解常微分方程（组）

2.1 一阶常微分方程（组）模型

给定初始条件的一阶常微分方程（组）的标准形式是：
$$\{\begin{array}{l}\begin{array}{rl}& \frac{dy}{dt}=f(y,t)\\ & y(t_0)=y_0\end{array}\end{array}$$

式中的 y 在常微分方程中是标量，在常微分方程组中是数组向量。

2.2 scipy.integrate.odeint() 函数

SciPy 提供了两种方式求解常微分方程：基于 odeint 函数的 API 比较简单易学，基于 ode 类的面向对象的 API 更加灵活。

**scipy.integrate.odeint() **是求解微分方程的具体方法，通过数值积分来求解常微分方程组。在 odeint 函数内部使用 FORTRAN 库 odepack 中的 lsoda，可以求解一阶刚性系统和非刚性系统的初值问题。官网介绍详见： scipy.integrate.odeint — SciPy v1.6.3 Reference Guide 。

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

odeint 的主要参数：

求解标准形式的微分方程（组）主要使用前三个参数：

• func: callable(y, t, …) 　　导数函数 $f(y,t)$ ，即 y 在 t 处的导数，以函数的形式表示
• y0: array：　　初始条件 $y_0$，对于常微分方程组 $y_0$ 则为数组向量
• t: array：　　求解函数值对应的时间点的序列。序列的第一个元素是与初始条件 $y_0$ 对应的初始时间 $t_0$；时间序列必须是单调递增或单调递减的，允许重复值。

其它参数简介如下：

• args: 向导数函数 func 传递参数。当导数函数 $f(y,t,p1,p2,..)$ 包括可变参数 p1,p2… 时，通过 args =(p1,p2,…) 可以将参数p1,p2… 传递给导数函数 func。argus 的用法参见 2.4 中的实例2。

• Dfun: func 的雅可比矩阵，行优先。如果 Dfun 未给出，则算法自动推导。

• col_deriv: 自动推导 Dfun的方式。

• printmessg: 布尔值。控制是否打印收敛信息。

• 其它参数用于控制求解算法的参数，一般情况可以忽略。

odeint 的主要返回值：

• y: array 　　数组，形状为 (len(t),len(y0)，给出时间序列 t 中每个时刻的 y 值。

---

3. 实例1：Scipy 求解一阶常微分方程

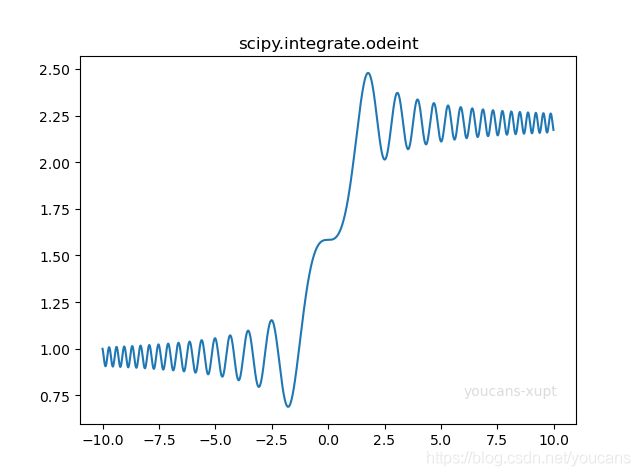
3.1 例题 1：求微分方程的数值解

$$\{\begin{array}{l}\begin{array}{rl}& \frac{dy}{dt}=sin(t^2)\\ & y(-10)=1\end{array}\end{array}$$

3.2 常微分方程的编程步骤

以该题为例讲解 scipy.integrate.odeint() 求解常微分方程初值问题的步骤：

1. 导入 scipy、numpy、matplotlib 包；

2. 定义导数函数 $f(y,t)=sin(t^2)$ ；

3. 定义初值 $y_0$ 和 $y$ 的定义区间 $[t_0,t]$；

4. 调用 odeint() 求 $y$ 在定义区间 $[t_0,t]$ 的数值解。

3.3 Python 例程

# 1. 求解微分方程初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

def dy_dt(y, t):  # 定义函数 f(y,t)
    return np.sin(t**2)

y0 = [1]  # y0 = 1 也可以
t = np.arange(-10,10,0.01)  # (start,stop,step)
y = odeint(dy_dt, y0, t)  # 求解微分方程初值问题

# 绘图
plt.plot(t, y)
plt.title("scipy.integrate.odeint")
plt.show()

3.4 Python 例程运行结果

---

4. 实例2：Scipy 求解一阶常微分方程组

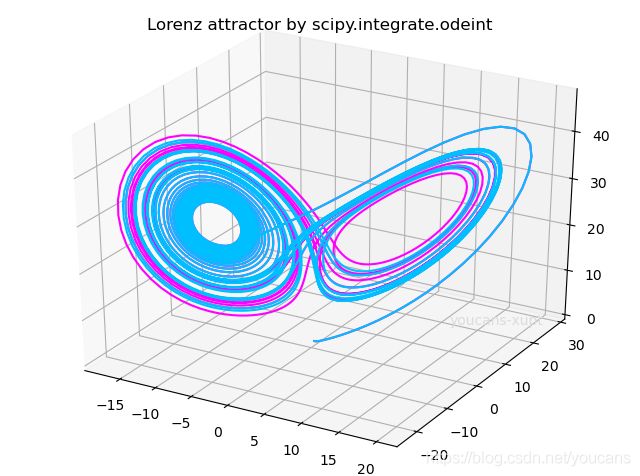
4.1 例题 2：求洛伦兹（Lorenz）方程的数值解

洛伦兹（Lorenz）混沌吸引子的轨迹可以由如下的 3个微分方程描述：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{dx}{dt}=\sigma (y-x)\\ & \frac{dy}{dt}=x(\rho -z)-y\\ & \frac{dz}{dt}=xy-\beta z\end{array}\end{array}$$

洛伦兹方程将大气流体运动的强度 x 与水平和垂直方向的温度变化 y 和 z 联系起来，进行大气对流系统的模拟，现已广泛应用于天气预报、空气污染和全球气候变化的研究。参数 $\sigma$ 称为普兰特数，$\rho$ 是规范化的瑞利数，$\beta$ 和几何形状相关。洛伦兹方程是非线性微分方程组，无法求出解析解，只能使用数值方法求解。

4.2 洛伦兹（Lorenz）方程问题的编程步骤

以该题为例讲解 scipy.integrate.odeint() 求解常微分方程初值问题的步骤：

1. 导入 scipy、numpy、matplotlib 包；

2. 定义导数函数 lorenz(W, t, p, r, b)

   注意 odeint() 函数中定义导数函数的标准形式是 $f(y,t)$ ，对于微分方程组 y 表示向量。

   为避免混淆，我们记为 $W=[x,y,z]$，函数 lorenz(W,t) 定义导数函数 $f(W,t)$ 。

   用 p,r,b 分别表示方程中的参数 $\sigma 、\rho 、\beta$，则对导数定义函数编程如下：

# 导数函数，求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W,t,p,r,b):
    x, y, z = W  # W=[x,y,z]
    dx_dt = p*(y-x)  # dx/dt = p*(y-x), p: sigma
    dy_dt = x*(r-z) - y  # dy/dt = x*(r-z)-y, r:rho
    dz_dt = x*y - b*z  # dz/dt = x*y - b*z, b;beta
    return np.array([dx_dt,dy_dt,dz_dt])

3. 定义初值 $W_0$ 和 $W$ 的定义区间 $[t_0,t]$；

4. 调用 odeint() 求 $W$ 在定义区间 $[t_0,t]$ 的数值解。

   注意例程中通过 args=paras 或 args = (10.0,28.0,3.0) 将参数 (p,r,b) 传递给导数函数 lorenz(W,t,p,r,b)。参数 (p,r,b) 当然也可以不作为函数参数传递，而是在导数函数 lorenz() 中直接设置。但例程的参数传递方法，使导数函数结构清晰、更为通用。另外，对于可变参数问题，使用这种参数传递方式就非常方便。

4.3 洛伦兹（Lorenz）方程问题 Python 例程

# 2. 求解微分方程组初值问题(scipy.integrate.odeint)
from scipy.integrate import odeint    # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 导数函数, 求 W=[x,y,z] 点的导数 dW/dt
def lorenz(W,t,p,r,b):  # by youcans
    x, y, z = W  # W=[x,y,z]
    dx_dt = p*(y-x)  # dx/dt = p*(y-x), p: sigma
    dy_dt = x*(r-z) - y  # dy/dt = x*(r-z)-y, r:rho
    dz_dt = x*y - b*z  # dz/dt = x*y - b*z, b;beta
    return np.array([dx_dt,dy_dt,dz_dt])

t = np.arange(0, 30, 0.01)  # 创建时间点 (start,stop,step)
paras = (10.0, 28.0, 3.0)  # 设置 Lorenz 方程中的参数 (p,r,b)

# 调用ode对lorenz进行求解, 用两个不同的初始值 W1、W2 分别求解
W1 = (0.0, 1.00, 0.0)  # 定义初值为 W1
track1 = odeint(lorenz, W1, t, args=(10.0, 28.0, 3.0))  # args 设置导数函数的参数
W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2], color='magenta') # 绘制轨迹 1
ax.plot(track2[:,0], track2[:,1], track2[:,2], color='deepskyblue') # 绘制轨迹 2
ax.set_title("Lorenz attractor by scipy.integrate.odeint")
plt.show()

4.4 洛伦兹（Lorenz）方程问题 Python 例程运行结果

---

5. 实例3：Scipy 求解高阶常微分方程

高阶常微分方程，必须做变量替换，化为一阶微分方程组，再用 odeint 求数值解。

5.1 例题 3：求二阶 RLC 振荡电路的数值解

零输入响应的 RLC 振荡电路可以由如下的二阶微分方程描述：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{d^{2}u}{d{t}^2}+\frac{R}{L}\ast \frac{du}{dt}+\frac{1}{LC}\ast u=0\\ & u(0)=U_0\\ & u^{\prime }(0)=0\end{array}\end{array}$$

令 $ \alpha = R/2L$、$\omega_0^2=1/LC$，在零输入响应 $u_s=0$ 时上式可以写成：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{d^{2}u}{d{t}^2}+2\alpha \frac{du}{dt}+{\omega }_0^{2}u=0\\ & u(0)=U_0\\ & u^{\prime }(0)=0\end{array}\end{array}$$
对二阶微分方程问题，引入变量 $v=du/dt$，通过变量替换就把原方程化为如下的微分方程组：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{du}{dt}=v\\ & \frac{dv}{dt}=-2\alpha v-{\omega }_0^{2}u\\ & u(0)=U_0\\ & v(0)=0\end{array}\end{array}$$

这样就可以用上节求解微分方程组的方法来求解高阶微分方程问题。

5.2 二阶微分方程问题的编程步骤

以RLC 振荡电路为例讲解 scipy.integrate.odeint() 求解高阶常微分方程初值问题的步骤：

1. 导入 scipy、numpy、matplotlib 包；

2. 定义导数函数 deriv(Y, t, a, w)

   注意 odeint() 函数中定义导数函数的标准形式是 $f(y,t)$ ，本问题中 y 表示向量，记为 $Y=[u,v]$

   导数定义函数 deriv(Y, t, a, w) 编程如下，其中 a, w 分别表示方程中的参数 $\alpha 、\omega$：

# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2*a*v-w*w*u]
    return dY_dt

3. 定义初值 $Y_0=[u_0,v_0]$ 和 $Y$ 的定义区间 $[t_0,t]$；

4. 调用 odeint() 求 $Y=[u,v]$ 在定义区间 $[t_0,t]$ 的数值解。

   例程中通过 args=paras 将参数 (a,w) 传递给导数函数 deriv(Y, t, a, w) 。本例要考察不同参数对结果的影响，这种参数传递方法使用非常方便。

5.3 二阶微分方程问题 Python 例程

# 3. 求解二阶微分方程初值问题(scipy.integrate.odeint)
# Second ODE by scipy.integrate.odeint
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2*a*v-w*w*u]
    return dY_dt

t = np.arange(0, 20, 0.01)  # 创建时间点 (start,stop,step)
# 设置导数函数中的参数 (a, w)
paras1 = (1, 0.6)  # 过阻尼：a^2 - w^2 > 0
paras2 = (1, 1)  # 临界阻尼：a^2 - w^2 = 0
paras3 = (0.3, 1)  # 欠阻尼：a^2 - w^2 < 0

# 调用ode对进行求解, 用两个不同的初始值 W1、W2 分别求解
Y0 = (1.0, 0.0)  # 定义初值为 Y0=[u0,v0]
Y1 = odeint(deriv, Y0, t, args=paras1)  # args 设置导数函数的参数
Y2 = odeint(deriv, Y0, t, args=paras2)  # args 设置导数函数的参数
Y3 = odeint(deriv, Y0, t, args=paras3)  # args 设置导数函数的参数
# W2 = (0.0, 1.01, 0.0)  # 定义初值为 W2
# track2 = odeint(lorenz, W2, t, args=paras)  # 通过 paras 传递导数函数的参数

# 绘图
plt.plot(t, Y1[:, 0], 'r-', label='u1(t)')
plt.plot(t, Y2[:, 0], 'b-', label='u2(t)')
plt.plot(t, Y3[:, 0], 'g-', label='u3(t)')
plt.plot(t, Y1[:, 1], 'r:', label='v1(t)')
plt.plot(t, Y2[:, 1], 'b:', label='v2(t)')
plt.plot(t, Y3[:, 1], 'g:', label='v3(t)')
plt.axis([0, 20, -0.8, 1.2])
plt.legend(loc='best')
plt.title("Second ODE by scipy.integrate.odeint")
plt.show()

5.4 二阶方程问题 Python 例程运行结果

结果讨论：

RLC串联电路是典型的二阶系统，在零输入条件下根据 $\alpha$ 与 $\omega$ 的关系，电路的输出响应存在四种情况：

1. 过阻尼： ${\alpha }^2-{\omega }^2>0$ ，有 2 个不相等的负实数根；
2. 临界阻尼： ${\alpha }^2-{\omega }^2=0$，有 2 个相等的负实数根；
3. 欠阻尼： ${\alpha }^2-{\omega }^2<0$，有一对共轭复数根；
4. 无阻尼：$R=0$，有一对纯虚根。

例程中所选择的 3 组参数分别对应过阻尼、临界阻尼和欠阻尼的条件，微分方程的数值结果很好地体现了不同情况的相应曲线。

---

6. 小结

1. 小白首先要有信心，用 Scipy 工具包求解标准形式的微分方程（组），编程实现是非常简单、容易掌握的。
2. 其次要认识到，由于微分方程的解的特性是与模型参数密切相关的，不同参数的解可能具有完全不同的形态。这就涉及模型稳定性、灵敏度的分析，很容易使论文写的非常丰富和精彩。
3. 不会从问题建立微分方程模型怎么办，不会展开参数对稳定性、灵敏度的影响进行讨论怎么办？谁让你自己做呢，当然是先去找相关专业的教材、论文，从中选择比较接近、比较简单的理论和模型，然后通过各种假设强行将题目简化为模型中的条件，这就可以照猫画虎了。

【本节完】

版权声明：

欢迎关注『Python小白的数学建模课 @ Youcans』 原创作品

原创作品，转载必须标注原文链接：(https://blog.csdn.net/youcans/article/details/117702996)。

Copyright 2021 Youcans, XUPT

Crated：2021-06-08

欢迎关注『Python小白的数学建模课 @ Youcans』系列，每周持续更新
Python小白的数学建模课-A1.国赛赛题类型分析
Python小白的数学建模课-A2.2021年数维杯C题探讨
Python小白的数学建模课-A3.12个新冠疫情数模竞赛赛题及短评
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python小白的数学建模课-04.整数规划
Python小白的数学建模课-05.0-1规划
Python小白的数学建模课-06.固定费用问题
Python小白的数学建模课-07.选址问题
Python小白的数学建模课-09.微分方程模型
Python数模笔记-StatsModels 统计回归
Python数模笔记-Sklearn（5）支持向量机
Python数模笔记-NetworkX（5）关键路径法
Python数模笔记-模拟退火算法（4）旅行商问题