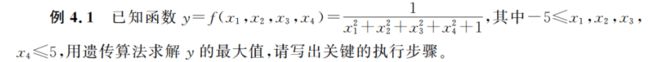就这?智能优化算法《计算智能》张军 超详细讲解
别只收藏不点赞的啊,一键三连走起来!
前言
由于最近新参与了一个与智能优化相关的科研课题,所以需要了解一些计算智能的算法知识。经老师推荐,从网上购买了张军老师的这本《计算智能》,尽管出版年份距今已有一些年日,但因该领域多年来并未有太多新的大改变,且该书对新手相对友好,故仍具很大研读价值。
整理感悟:静下心来学,世界一切都变得那么美好。
希望大家也能沉下心来,学完这本书,或者看完这篇博客。共勉!
(需要算法源码的朋友可以关注并点赞收藏,留下你的邮箱,我会第一时间将源码发给你)
目录
- 前言
- 第1章 绪论
-
- 1.1 最优化问题
- 1.1.1 函数优化问题
- 1.1.2 组合优化问题
- 1.2.1 计算复杂性
- 1.2.2 NP理论
- 1.3 计算智能方法
- 1.3.1 计算智能的分类与理论
- 1.3.2 计算智能的研究与发展
- 1.3.3 计算智能的特征与应用
- 第2章 神经网络
-
- 2.1.1 基本原理
- 2.1.2 研究进展
- 2.2 神经网络的典型结构
- 2.2.1 单层感知器网络
- 2.2.2 前馈型网络
- 2.2.3 前馈内层互联网络
- 2.2.4 反馈型网络
- 2.2.5 全互联网络
- 2.3 神经网络的学习算法
- 2.3.1 学习方法
- 2.3.2 学习规则
- 2.4 BP神经网络
- 2.4.1 基本思想
- 2.4.2 算法流程
- 2.5 进化神经网络
- 2.6 神经网络的应用
- 第3章 模糊逻辑
-
- 为什么需要模糊逻辑
- 3.1 模糊逻辑简介
- 3.2 模糊集合与模糊逻辑
- 3.2.1 模糊集合与隶属度函数
- 3.2.2 模糊集合上的运算定律
- 3.2.3 模糊逻辑
- 3.2.4 模糊关系及其合成运算
- 3.3 模糊推理
- 3.3.1 模糊规则、语言变量和语言算子
- 3.4 模糊计算的流程
- 3.5 模糊逻辑的应用
- 第4章 遗传算法
-
- 4.1 遗传算法简介
- 4.1.1 基本原理
- 4.1.2 研究进展
- 4.2 遗传算法的流程
- 4.3 遗传算法的改进
- 4.3.1 算子选择
- 4.3.2 参数设置
- 4.3.3 混合遗传算法
- 4.3.4 并行遗传算法
- 4.4 遗传算法的应用
- 第5章 蚁群优化算法
-
- 5.1 基本原理
- 5.2 算法流程
- 5.2.1 基本流程
- 5.2.2 应用举例
- 5.3 改进版本
- 5.3.1 精华蚂蚁系统
- 5.3.2 基于排列的蚂蚁系统
- 5.3.3 最大最小蚂蚁系统
- 5.3.4 蚁群系统
- 5.3.5 连续正交蚁群系统
- 5.4 参数设置
- 第6章 粒子群优化算法
-
- 6.1 粒子群优化算法简介
- 6.1.1 思想来源
- 6.1.2 基本原理
- 6.2.1 基本流程
- 6.2.2 应用举例
- 6.3 粒子群优化算法的改进研究
- 6.3.1 理论研究改进
- 6.3.2 拓扑结构改进
- 6.3.3 混合算法改进
- 6.3.4 离散版本改进
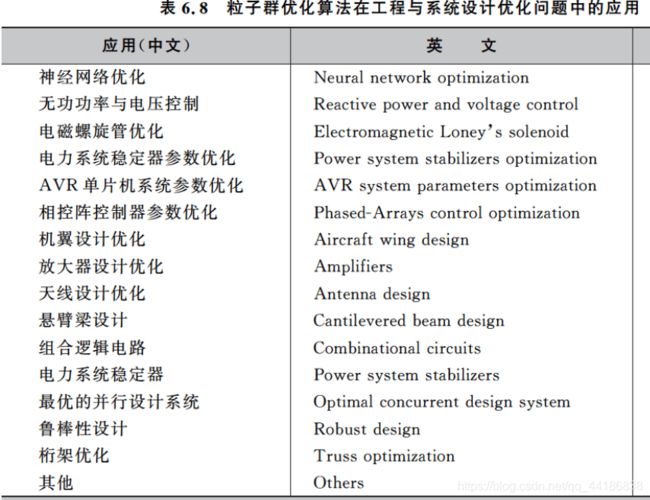
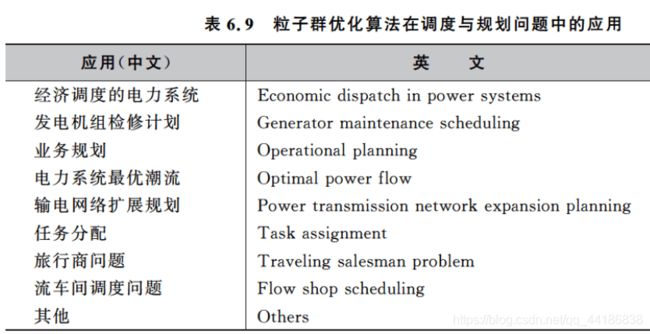
- 6.4 相关应用
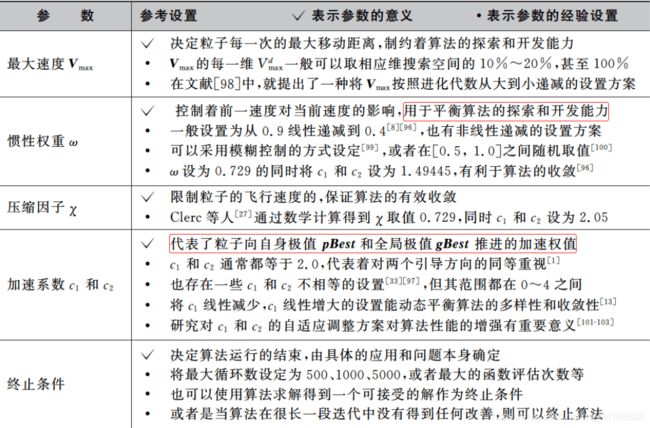
- 6.5 参数设置
- 第7章 免疫算法
-
- 7.1 算法简介
- 7.1.1 思想来源
- 7.1.2 免疫算法的生物模型
- 7.1.3 二进制模型
- 7.2 免疫算法的基本流程
- 7.2.1 基本流程
- 7.2.2 更一般的基本免疫算法
- 7.3 常用免疫算法
- 7.3.1 负选择算法
- 7.3.2 克隆选择算法
- 7.3.3 免疫算法与智能计算
- 7.4 免疫算法的应用
- 第8章 分布估计算法
-
- 8.1 分布估计算法简介
- 8.1.1 产生背景
- 8.1.2 分布估计算法的发展历史
- 8.2 基本流程
- 8.2.1 基本的分布估计算法
- 8.2.2 一个简单分布估计算的例子
- 8.3 分布估计算法的改进及理论研究
- 8.3.1 概率模型的改进
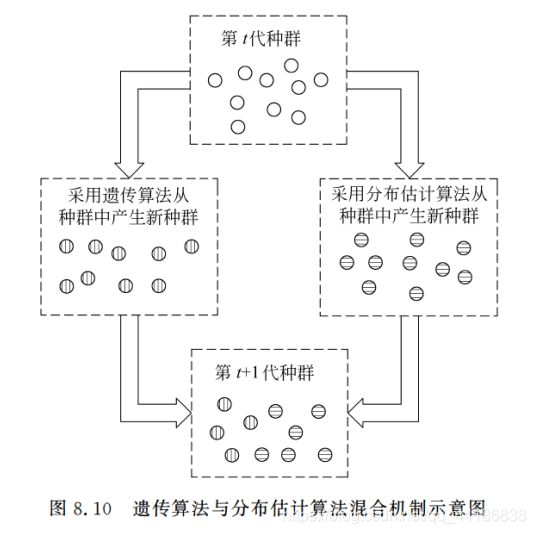
- 8.3.2 混合分布估计算法
- 8.3.3 并行分布估计算法
- 8.4 分布估计算法的应用
- 第9章 Memetic算法
-
- 9.1 Memetic算法的基本思想
- 9.2 Memetic算法的框架
- 9.3 静态Memetic算法
- 9.3.1 局部搜索的位置
- 9.3.2 Lamarckian模式Baldwinian模式
- 9.4 动态Memetic算法
- 9.4.1 动态Memetic算法
- 9.4.2 Meta-Lamarckian学习型MA
- 9.4.3 超启发式Memetic算法
- 9.4.4 协同进化Memetic算法
- 第10章 模拟退火与禁忌搜索
-
- 10.1 模拟退火算法
- 10.1.1 算法思想
- 10.1.2 基本流程
- 10.1.3 应用举例
- 10.2 禁忌搜索算法
- 10.2.1 算法思想
- 10.2.2 基本流程
- 10.2.3 应用举例
- 结束语
第1章 绪论
1.1 最优化问题
最优化问题的求解模型如下公式所示:
![]()
其中D是问题的解空间,X是D中的一个合法解。一般可将X表示为X = (x1, x2, …, xn),表示一组决策变量。
最优化问题就是在解空间中寻找一个合法的解X(一组最佳的决策变量),使得X对应的函数映射值f(X)最小(最大)。
简单理解的话,就是把f(x)看做花费值,怎么让你花的最少,就是最优化问题。
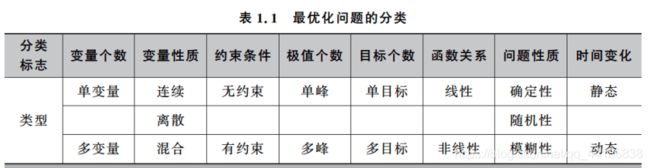
根据决策变量xi的取值类型,我们可以将最优化问题分为函数优化问题和组合优化问题两大类。
决策变量均为连续变量的最优化问题为函数优化问题,而均为离散变量的最优化问题则为组合优化问题。
啥?不懂什么是函数优化问题和什么是组合优化问题?没事,这下面不就准备跟你讲了嘛。
1.1.1 函数优化问题

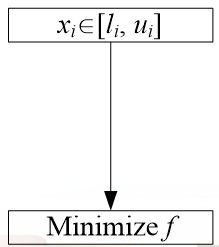
例如:
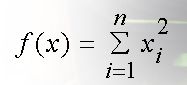
其中,n=30表示问题空间的维数,xi∈ [-100,100]是定义域,这个函数的最小值为0。
那这其实就是一个最简单的函数优化问题,对应上文所讲的“连续变量”。
那啥时候需要用到函数优化问题呢?
其实很多情况下都会遇到,也不知道你们是不是曾经沦为过无情的模型调参机器人(反正我是有过呜呜呜)
很多科学实验参数配置和工农业生产实践都需要面临这种类型的最优化问题,像是设计神经网络的过程中,需要确定神经元节点间的网络连接权重,从而使得网络性能达到最优。
在这种问题中,需要优化的变量的取值是某个连续区间上的值,是一个实数。各个决策变量之间可能是独立的,也可能是相互关联、相互制约的,它们的取值组合构成了问题的一个解。
由于决策变量是连续值,因此对每个变量进行枚举是不可能的。在这种情况下,必须借助最优化方法对问题进行求解。
1.1.2 组合优化问题
其实组合优化问题我想大家肯定是遇到过的,因为可能现在在看这篇博客的同学都学过了算法程序设计或者数据结构等的课程。那么你们肯定见过所谓的0-1背包问题,这个问题就是很典型的组合优化问题。当然啦还有旅行商问题等也属于组合优化问题。
很多离散组合优化问题都是从运筹学(Operations Research,OR)中演化出来的。
组合优化其所研究的问题涉及到信息技术、经济管理、工业工程、交通运输、通信网络等众多领域,在科学研究和生产实践中都起着重要的作用。
我们不难发现,其实这些问题解决的方法其实很简单,比方说0-1背包,那无非就是n个物品,每个物品要么带要么不带,即为2^n的情况,得到所有情况然后取出价值最大的那种方法就可以了。
是呀,这样子的话真的是老简单了。
哈哈,开个玩笑。只要是稍微多想一想都能发现我们上述的穷举法有一个很致命的问题,就是当你的n值过大时,对应的计算量可是呈指数暴增的。
所以这个时候,就需要我们借助智能优化计算方法,可以在合理的时间内求解得到令人满意的解,从而满足实践的需要。
对于算法的计算复杂性,我们一般很容易进行判断,例如使用蛮力法去枚举旅行商问题或者0-1背包问题的算法,就是具有指数计算复杂性的算法。
诶,啥是计算复杂性?下文介绍。
1.2.1 计算复杂性
啥是计算复杂性呢?
简单讲就是用来描述求解问题的难易程度或者算法执行效率的高低。
对于算法的计算复杂性,我们一般很容易进行判断,例如使用蛮力法去枚举旅行商问题或者0-1背包问题的算法,就是具有指数计算复杂性的算法。
对于某问题的计算复杂性进行判断却不是一件简单的事情。
问题的计算复杂性是问题规模的函数,故需要首先定义问题的规模。
例如对于矩阵运算,矩阵的阶数可被作为问题的规模。
(1)如果求解一个问题需要的运算次数或步骤数是问题规模n的指数函数,则称该问题有指数时间复杂性。
(2)如果所需的运算次数是n的多项式函数,则称它有多项式时间复杂性。
对于某个具体问题,其复杂性上界是已知求解该问题的最快算法的复杂性,而复杂性下界只能通过理论证明来建立。
证明一个问题的复杂性下界就需要证明不存在任何复杂性低于下界的算法。显然,建立下界要比确定上界困难得多。
1.2.2 NP理论
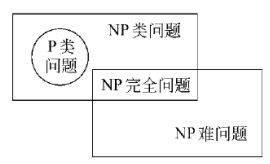
下面将介绍几种属于NP类别的问题,并会讲述其之间的关系。
P类问题是指一类能够用确定性算法在多项式时间内求解的判定问题。其实,在非正式的定义中,我们可以把那些在多项式时间内求解的问题当作P类问题。
NP类问题(Non-deterministic Polynomial Problem)
NP类问题是指一类可以用不确定性多项式算法求解的判定问题。例如旅行商问题的判定版本就是一个NP类问题。我们虽然还不能找到一个多项式的确定性算法求解最小的周游路线,但是可以在一个多项式时间内对任意生成的一条“路线”判定是否是合法(经过每个城市一次且仅仅一次)。比较P类问题和NP类问题的定义,我们很容易得到一个结论:P ⊆ \subseteq ⊆NP。
NP完全问题(NP Complete Problem)
我们称一个判定问题D是NP完全问题,条件是:
(1)D属于NP类;
(2)NP中的任何问题都能够在多项式时间内转化为D。
另外,一个满足条件(2)但不满足条件(1)的问题被称为NP难问题。也就是说,NP难问题不一定是NP类问题,例如图灵停机问题。正式地说,一个NP难问题至少跟NP完全问题一样难,也许更难!例如在某些任意大的棋盘游戏走出必胜的下法,就是一个NP难的问题,这个问题甚至比那些NP完全问题还难。
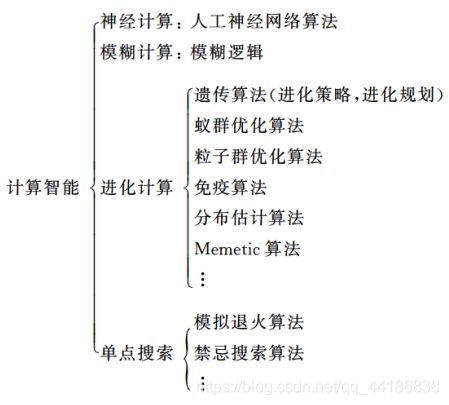
1.3 计算智能方法
计算智能算法是人工智能的一个分支,是联结主义的典型代表,又称为仿生学派或生理学派。
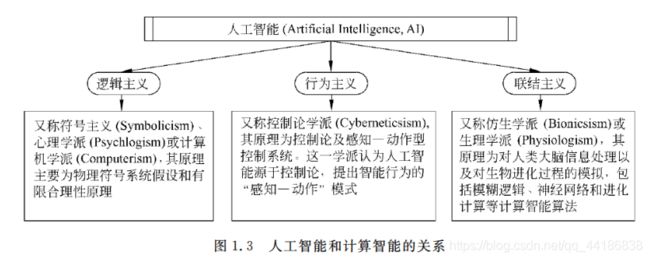
下面简单讲下计算智能的存在目的及意义:
随着技术的进步、工程实践问题变得越来越复杂,传统的计算方法面临着计算复杂度高、计算时间长等问题(如上文提到的0-1背包穷举法)。
那么,计算智能啥作用呢?
(1)计算智能方法采用启发式的随机搜索策略,在问题的全局空间中进行搜索寻优,能在可接受的时间内找到全局最优解或者可接受解。
(2)计算智能算法在处理优化问题的时候,对求解问题不需要严格的数学推导,而且有很好的全局搜索能力,具有普遍的适应性和求解的鲁棒性。
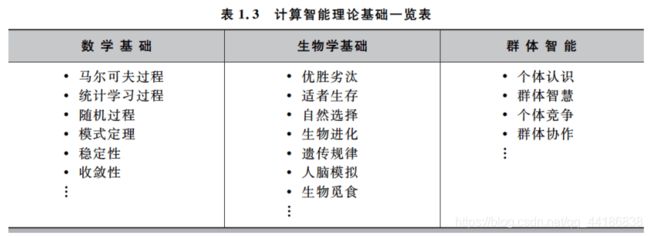
1.3.1 计算智能的分类与理论
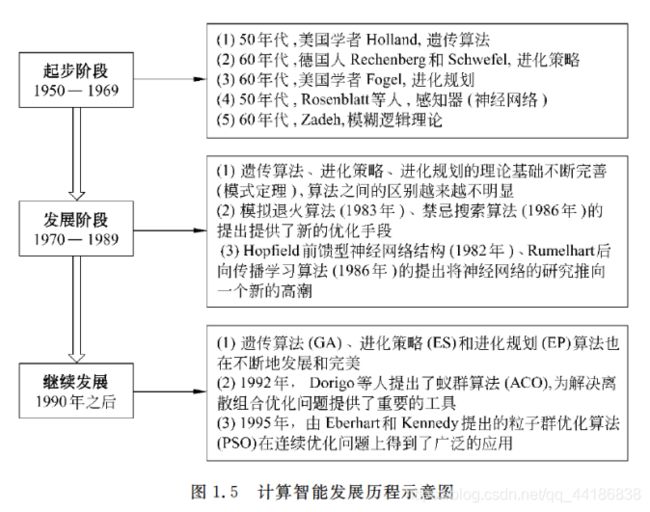
1.3.2 计算智能的研究与发展
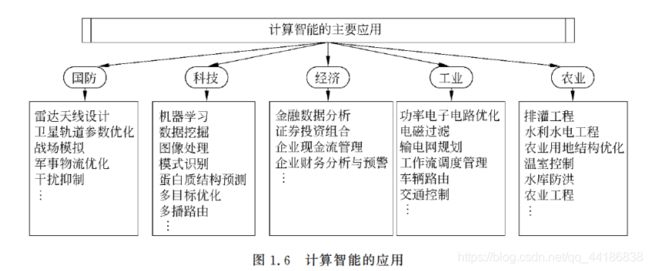
1.3.3 计算智能的特征与应用
第2章 神经网络
说实话昂,神经网络这东西大家可能或多或少都有接触过了,而且这本书由于年代久远,所以一些专业词汇也跟我们现在有些许不同。
但说实话论基础知识来说的话,讲的是真滴详细,我就当复复习咯。
2.1.1 基本原理
神经网络(Neural Network,NN)一般也称为人工神经网络(Artificial Neural Network,ANN)。
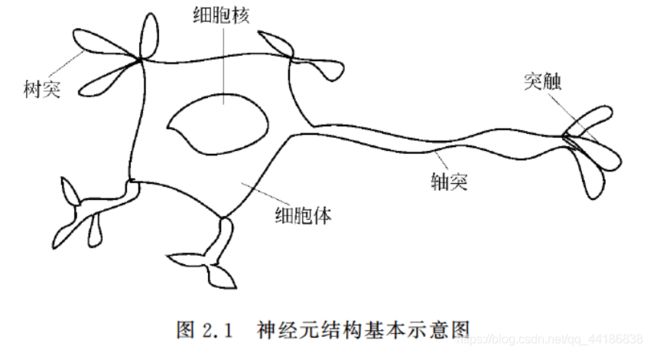
书中前部分花了大幅篇章讲述生物学知识,如上述图中的轴突树突细胞体等,看了难免会回忆当初高中。
不过这里就不赘述相关生物知识了,放下生物神经元与人工神经元关系对照表以及人工神经元结构及功能示意图。
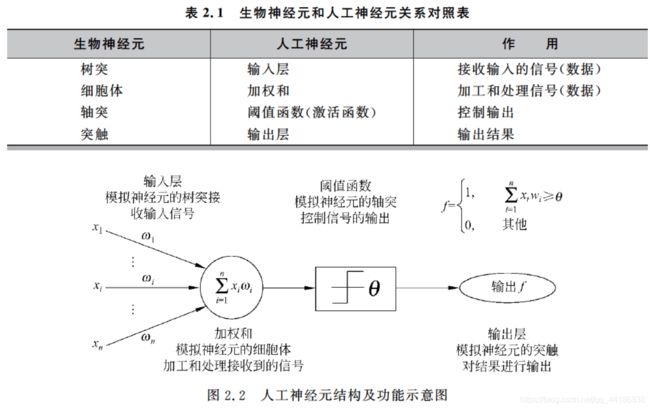
从图中我们也大致可以看出人工神经元是如何模仿生物的神经元进行工作的。
2.1.2 研究进展
这就没啥好说的了,毕竟距今十来年了。。。
反正大家应该也都知道现在神经网络和深度学习有多么火了哈哈。
2.2 神经网络的典型结构
按网络的结构区分
前向网络
反馈网络
按学习方式区分
有教师(监督)学习网络
无教师(监督)学习网络
按网络的性能区分
连续型和离散型网络
随机型和确定型网络
按突触性质区分
一阶线性关联网络
高阶非线性关联网络
按对生物神经系统的层次模拟区分
神经元层次模型
组合式模型
网络层次模型
神经系统层次模型
智能型模型
2.2.1 单层感知器网络
单层感知器是最早使用的,也是最简单的神经网络结构,由一个或多个线性阈值单元组成。
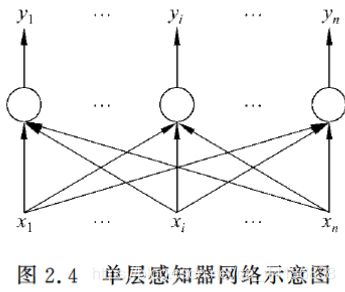
由于这种网络结构相对简单,因此能力也非常的有限,一般比较少用。
2.2.2 前馈型网络
前馈型网络的信号由输入层到输出层单向传输。
每层的神经元仅与其前一层的神经元相连,仅接受前一层传输来的信息。
是一种当时最为广泛使用的神经网络模型,因为它本身的结构也不太复杂,学习和调整方案也比较容易操作,而且由于采用了多层的网络结构,其求解问题的能力也得到明显的加强,基本上可以满足使用要求。
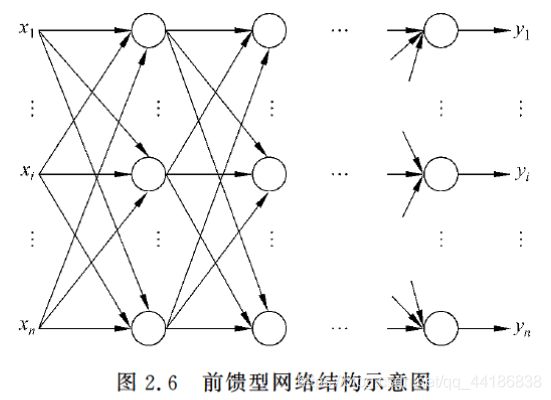
2.2.3 前馈内层互联网络
这种网络结构从外部看还是一个前馈型的网络,但是内部有一些节点在层内互连。
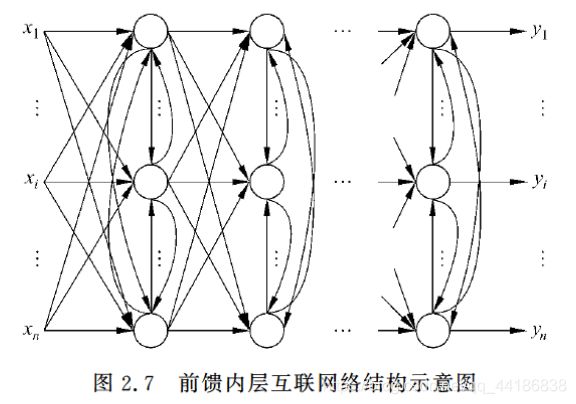
2.2.4 反馈型网络
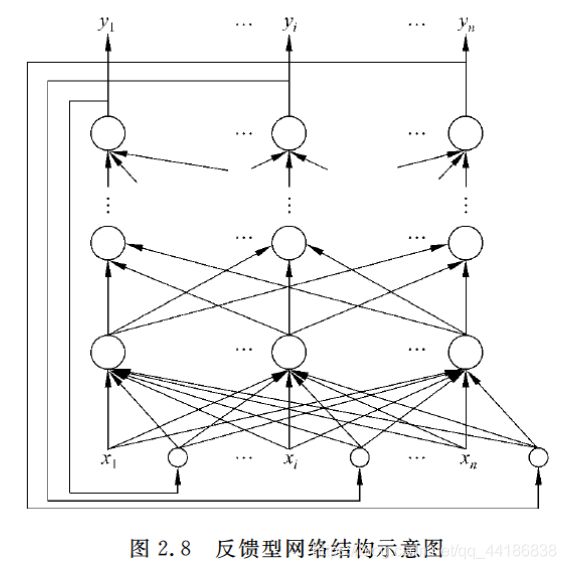
这种网络结构在输入输出之间还建立了另外一种关系,就是网络的输出层存在一个反馈回路到输入层作为输入层的一个输入,而网络本身还是前馈型的。
这种神经网络的输入层不仅接受外界的输入信号,同时接受网络自身的输出信号。输出反馈信号可以是原始输出信号,也可以是经过转化的输出信号;可以是本时刻的输出信号,也可以是经过一定延迟的输出信号。
此种网络经常用于系统控制、实时信号处理等需要根据系统当前状态进行调节的场合。
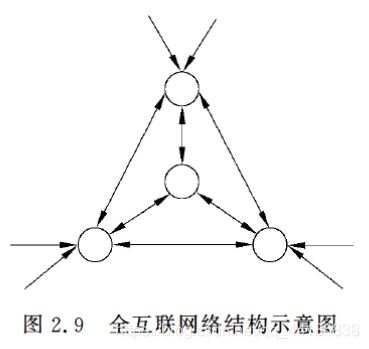
2.2.5 全互联网络
如Hopfiled和Boltgmann网络都是这种类型。
2.3 神经网络的学习算法

讲实话,这里面有不少学习规则是我自始至终没有听说过的。所以学习一下新知识也未尝不可。
2.3.1 学习方法
说到这,就让我想到我另外一篇博客:https://blog.csdn.net/qq_44186838/article/details/107748555
这篇介绍的可要详细多了。
那这里我们简单提一下:
Supervised learning 监督学习
是有特征(feature)和标签(label)的,即便是没有标签的,机器也是可以通过特征和标签之间的关系,判断出标签。
Unsupervised learning 无监督学习
只有特征,没有标签。
Semi-Supervised learning 半监督学习
使用的数据,一部分是标记过的,而大部分是没有标记的。和监督学习相比较,半监督学习的成本较低,但是又能达到较高的准确度。
Reinforcement learning 强化学习
强化学习也是使用未标记的数据,但是可以通过一些方法知道你是离正确答案越来越近还是越来越远(奖惩函数)。
2.3.2 学习规则
Hebb学习规则
简单理解就是,如果处理单元从另一个处理单元接受到一个输入,并且如果两个单元都处于高度活动状态,这时两单元间的连接权重就要被加强。
Hebb学习规则是一种没有指导的学习方法,它只根据神经元连接间的激活水平改变权重,因此此这种方法又称为相关学习或并联学习。
Delta( δ \delta δ)学习规则
Delta规则是最常用的学习规则,其要点是改变单元间的连接权重来减小系统实际输出与应有的输出间的误差。
这个规则也叫Widrow-Hoff学习规则,首先在Adaline模型中应用,也可称为最小均方差规则。
BP网络的学习算法称为BP算法,是在Delta规则基础上发展起来的,可在多层网络上有效地学习。
梯度下降学习规则
梯度下降学习规则的要点为在学习过程中,保持误差曲线的梯度下降。
误差曲线可能会出现局部的最小值,在网络学习时,应尽可能摆脱误差的局部最小值,而达到真正的误差最小值 。
目前我们接触到的很多降低损失函数值的算法利用的就是梯度下降的学习规则。而梯度下降具体也有很多种类别,感兴趣的可以自行去了解哦。
Kohonen学习规则
该规则是由Teuvo Kohonen在研究生物系统学习的基础上提出的,只用于没有指导下训练的网络。
后向传播学习规则
后向传播(Back Propagation,BP)学习,是当时应用最为广泛的神经网络学习规则。
概率式学习规则
从统计力学、分子热力学和概率论中关于系统稳态能量的标准出发,进行神经网络学习的方式称概率式学习。
误差曲线可能会出现局部的最小值,在网络学习时,应尽可能摆脱误差的局部最小值,而达到真正的误差最小值 。
竞争式学习规则
竞争式学习属于无监督学习方式。这种学习方式是利用不同层间的神经元发生兴奋性联接以及同一层内距离很近的神经元间发生同样的兴奋性联接,而距离较远的神经无产生抑制性联接。
竞争式学习规则的本质在于神经网络中高层次的神经元对低层次神经元的输入模式进行竞争识别。
2.4 BP神经网络
2.4.1 基本思想
BP神经网络也称:后向传播学习的前馈型神经网络(Back Propagation Feed-forward Neural Network,BPFNN/BPNN),是一种应用最为广泛的神经网络。
在BPNN中,后向传播是一种学习算法,体现为BPNN的训练过程,该过程是需要教师指导的;前馈型网络是一种结构,体现为BPNN的网络构架。
反向传播算法通过迭代处理的方式,不断地调整连接神经元的网络权重,使得最终输出结果和预期结果的误差最小。
BPNN是一种典型的神经网络,广泛应用于各种分类系统,它也包括了训练和使用两个阶段。由于训练阶段是BPNN能够投入使用的基础和前提,而使用阶段本身是一个非常简单的过程,也就是给出输入,BPNN会根据已经训练好的参数进行运算,得到输出结果。
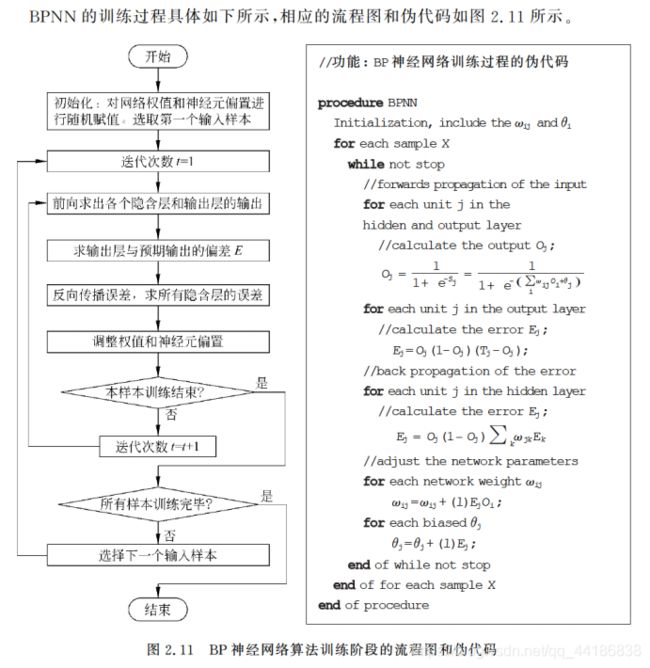
2.4.2 算法流程
(1)先是初始化网络权重,即参数的值。通常取值范围是-1.0-1.0。
(2)然后向前传播,计算每一层的输出(k层的输出即为k+1层的输入)。
(3)然后反向误差传播,什么意思呢?就是通过与预期输出的比较得到每个输出单元的误差,且得到的误差需要从后往前传播,前面一层的误差可以通过和它连接的后面的一层所有单元的误差计算所得,从后往前依次得到每一层每一个神经元的误差。
(4)然后进行网络权重与神经元偏置的调整。
![]()
![]()
其中l为学习率,通常取0-1之间的常数。
可能有些同学不太了解学习率,这里我简单讲一下。
其实学习率可以看做你每次要利用多少个误差点(即真实值与预测值不同的数据),学习率越低,损失函数的变化速度就越慢,容易过拟合。虽然使用低学习率可以确保我们不会错过任何局部极小值,但也意味着我们将花费更长的时间来进行收敛,特别是在被困在局部最优点的时候。而学习率过高容易发生梯度爆炸,loss振动幅度较大,模型难以收敛。
一个经验规则是将学习率设置为迭代次数t的倒数,也就是1/t。
(5)判断结束
当输出误差我们能够接受或者迭代达到我们规定的阈值时,选取下一个样本,继续重复(2)-(5)的工作,否则,迭代次数加1,然后转到(2)利用当前样本继续训练。
2.5 进化神经网络
还记得我在最开始提到的函数优化问题中到调参机器人吗?
对于某一具体问题,人工神经网络的设计是极其复杂的工作,至今仍没有系统的规律可以遵循。
目前,一般凭设计者主观经验与反复实验挑选ANN 设计所需的工具。
这样不仅使得设计工作的效率很低,而且还不能保证设计出的网络结构和权重等参数是最优的,从而造成资源的大量浪费和网络的性能低下。
这样就导致了我们成为了“无情的调参机器人”。
而进化神经网络,就可以帮助我们解决这样的问题。
使用进化算法去优化神经网络,通过进化算法和人工神经网络的结合使得神经网络能够在进化的过程中自适应地调整其连接权重、网络结构、学习规则等这些在使用神经网络的时候难以确定的参数,从而形成了进化神经网络(Evolutionary Neural Networks,ENN/EANN)。
进化算法和神经网络的结合给神经网络指明了新的发展方向,对突破神经网络结构复杂、参数难调等问题起到了重大的作用。
2.6 神经网络的应用
不多说,反正神经网络现在已经是无处不在了。
第3章 模糊逻辑
为什么需要模糊逻辑
著名的“沙堆问题”
“从一个沙堆里拿走一粒沙子,这还是一个沙堆吗?”
如果有人正正经经地问你这个问题,那你毫无疑问是会回答“是”。
但如果每拿一粒就问你这个问题,问题的答案会一直都是“是”吗?
如果每次都是拿走一粒,始终还是一个沙堆的话,那么到最后一粒沙都没有的沙堆也能成为沙堆咯。
这显然是违背我们认知的,那么这里的问题出在哪呢?
这里的问题就在于“沙堆”这个概念是模糊的,没有一个清晰的界限将“沙堆”与“非沙堆”分开。我们没有办法明确指出,在这个不断拿走沙子的过程中,什么时候“沙堆”不再是“沙堆”。
与“沙堆”相似的模糊概念还有“年轻人”、“小个子”、“大房子”等。这种在生活中常见的模糊概念,在用传统数学方法处理时,往往会出现问题。
那么,如果尝试消除这些概念的模糊性,会怎样呢?
如果规定沙堆只能由10000粒以上的沙子组成,“沙堆”这个概念的模糊性就消除了。10000粒沙子组成的是沙堆,9999粒沙子组成的不是沙堆:这在数学上没有任何问题。
然而,仅仅取走微不足道的一粒沙子,就将“沙堆”变为“非沙堆”,这又不符合我们日常生活中的思维习惯。
在企图用数学处理生活中的问题时,精确的数学语言和模糊的思维习惯产生了矛盾。
传统的数学方法常常试图进行精确定义,而人关于真实世界中事物的概念往往是模糊的,没有精确的界限和定义。在处理一些问题时,精确性和有效性形成了矛盾,诉诸精确性的传统数学方法变得无效,而具有模糊性的人类思维却能轻易解决。例如人脸识别问题。
所以,模糊逻辑就是用来解决这一矛盾的工具之一。
3.1 模糊逻辑简介
经典二值逻辑中,通常以0表示“假”以1表示“真”,一个命题非真即假 。
在模糊逻辑中,一个命题不再非真即假,它可以被认为是“部分的真” 。
模糊逻辑取消二值之间非此即彼的对立,用隶属度表示二值间的过度状态 。
打个比方,身高一米178是高个子。这句话无论你认为是真还是否,其实都是不准确的。
然后结合上文我们提到的隶属度,可以认为身高178对“高个子”的隶属度为0.7。
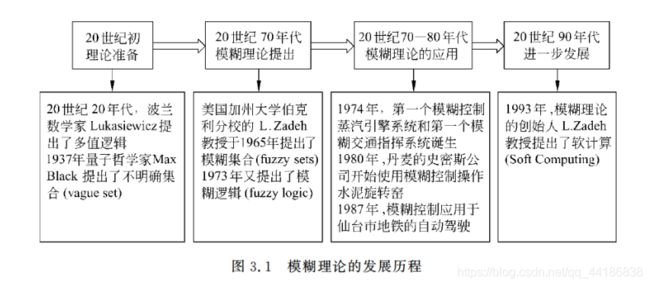
下文放一张模糊理论的发展历程图。
3.2 模糊集合与模糊逻辑
在介绍模糊集合之间,我们先来回忆一下我们之前学习过的古典集合。
古典集合:对于任意一个集合A,论域中的任何一个元素x,或者属于A,或者不属于A。集合A也可以由其特征函数定义:
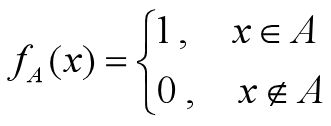
而模糊集合呢,则是论域上的元素可以“部分地属于”集合A 。一个元素属于集合A的程度称为隶属度,模糊集合可用隶属度函数定义。
模糊集合的完整定义如下:
设存在一个普通集合U,U到[0,1]区间的任一映射f都可以确定U的一个模糊子集,称为U上的模糊集合A。其中映射f叫做模糊集的隶属度函数,对于U上一个元素u, f(u)叫做u对于模糊集的隶属度,也可写作A(u) 。
看不懂这句话就多看几遍,哈哈。然后还可以结合下文的内容,增进理解。
3.2.1 模糊集合与隶属度函数
隶属度表示程度,它的值越大,表明u属于A的程度越高,反之则表明u属于A的程度越低 。
古典集合可以看作一种退化的模糊集合,即论域中不属于该古典集合的元素隶属度为0,其余元素隶属度为1。
模糊集合的表示法
一共有两种表示方法,分别如下所示。
(1)Zadeh表示法
当论域U为离散集合时,一个模糊集合可以表示为:
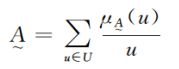
当论域U为连续集合时,一个模糊集合可以表示为:
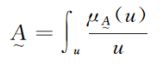
需要注意的是,这里仅仅是借用了求和与积分的符号,并不表示求和与积分。
(2)序对表示法
对于一个模糊集合来说,如果给出了论域上所有的元素以及其对应的隶属度,就等于表示出了该集合。所以,序对表示法出现了。
![]()
括号里面这两个是啥意思,我想不用多说了吧。
模糊集合表示法示例
书中给出了示例,来看一下。
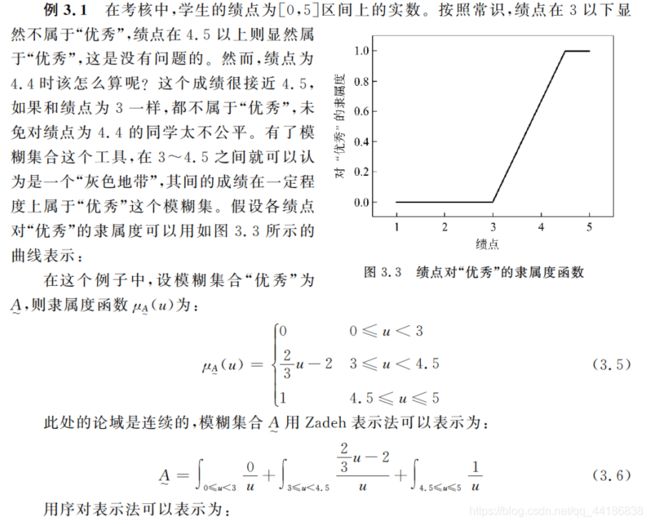
![]()
简单总结一下就是,模糊集合可以让很多情况的分类不显得那么绝对,而显得相对。
至于上文提到的隶属度函数,显而易见的是,隶属度函数十分重要,而不同问题对应的隶属度函数也不同,并且往往需要专家提供专业知识。
3.2.2 模糊集合上的运算定律
没啥好说的,基本同古典集合的运算定律一致。除了在古典集合中成立的矛盾律和排中律在模糊集合上不成立外。
定义:当且仅当对论域上任意元素u,都有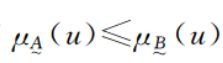
则称模糊集合A是模糊集合B的子集。
3.2.3 模糊逻辑
经典逻辑是二值逻辑,其中一个变元只有“真”和“假”(1和0)两种取值,其间不存在任何第三值。
模糊逻辑也属于一种多值逻辑,在模糊逻辑中,变元的值可以是[0,1]区间上的任意实数。
设P、Q为两个变元,模糊逻辑的基本运算定义如下:

3.2.4 模糊关系及其合成运算
模糊关系也是模糊集合上的一种映射。像经典关系一样,模糊关系上也定义了映射特有的合成运算。
设X,Y,Z为论域,R是X×Y上的模糊关系,S是Y×Z上的模糊关系,T是R到S的合成,记为T=R◦S,其隶属度函数定义如下:
![]()

这里稍微提一句,3.33这个公式后面会经常用到。
3.3 模糊推理
模糊推理可以认为是一种不精确的推理,是通过模糊规则将给定输入转化为输出的过程。
模糊推理是将输入的模糊集通过一定运算对应到特定输出模糊集的计算过程。模糊规则是在进行模糊推理时依赖的规则,通常可以用自然语言表述。
3.3.1 模糊规则、语言变量和语言算子
啥叫模糊规则?举个例子:“如果天气比较热,那么教室就应该开空调。”
但如果想具体了解模糊规则,那首先得了解一下几个概念。
语言变量 :对应于自然语言中的一个词或者一个短语、句子。它的取值就是模糊集合。

语言算子 :用于对模糊集进行修饰。作用类似于在自然语言常常的“可能”、“大约”、“比较”、“很”等,表示可能性、近似性和程度。
如果-则”规则 :模糊规则的一般形式。基础的“如果-则”规则表述如下:
If x is A then y is B(若x是A,那么y是B)
其中,设A的论域是U,B的论域是V,A与B均是语言变量的具体取值,即模糊集,x与y是变量名。规则中的“If x is A ”又称前件,“y is B”又称后件。“如果张三比较胖则运动量比较大”中,x就是“张三”,y为“运动量”,“比较胖”和“比较大”分别为x和y的取值之一。
模糊集A与B之间的关系是A×B上的模糊蕴含关系 ,记作A→ B,其定义有多种,常见的两种是最小运算(Mamdani)和积运算(Larsen)。
大家应该都听说过三段式推理吧,即:猫是人类的主人,小白是猫;结论:小白是人类的主人。
下面看下一个比较有趣的东西:
大前提(规则):若x是A,那么y是B。
小前提(输入):x是C。
结论(输出):y是 D。
???
如果你没接触古模糊推理的话,那肯定是???这种反应。那现在我们来具体解释一下。
即:在模糊推理中,小前提没有必要与大前提的前件一致(A与C不必完全一致),结论没有必要与大前提的后件一致(B与D不必完全一致)。
关于模糊蕴含的推理方式有两种:肯定式的推理和否定式的推理。下文将主要介绍肯定式推理。


上式中的合成操作有不同的定义方法,最常用的就是最大-最小合成。
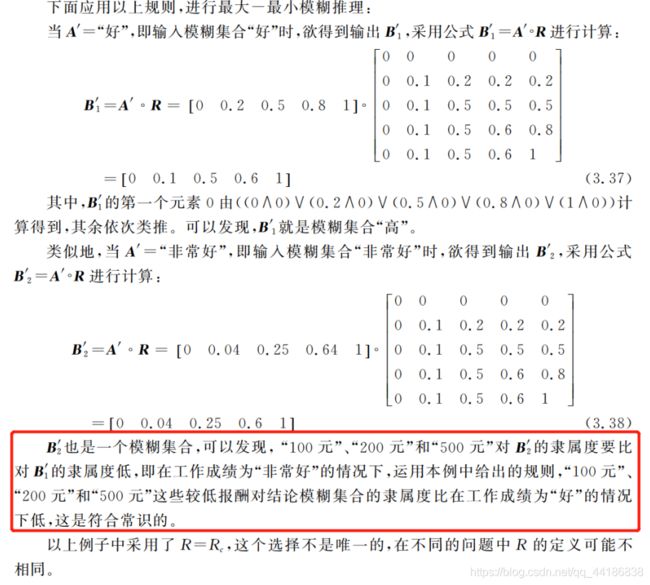
如果看到这不是很懂怎么操作的话,下面阔以看一下书中的这个实例。
稍微解释一下题中B’1的求解,这里就是用到了最大—最小合成。即:
![]()
3.4 模糊计算的流程
生活中经常能遇到这样的情况:要根据几个变量的输入,以及一组自然语言表述的经验规则,来决定输出。 这就是一个模糊计算的过程。
如现实生活中,我们在夏天往往会根据温度和湿度,决定开空调的温度。
模糊计算的过程可以分为四个模块:
模糊规则库、模糊化、推理方法和去模糊化
模糊规则库是专家提供的模糊规则。模糊化是根据隶属度函数从具体的输入得到对模糊集隶属度的过程。推理方法是从模糊规则和输入对相关模糊集的隶属度得到模糊结论的方法。去模糊化就是将模糊结论转化为具体的、精确的输出的过程。
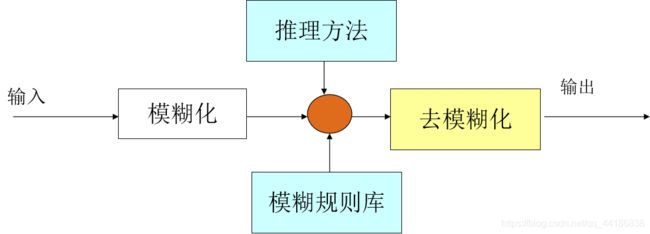
最后来看下实例。
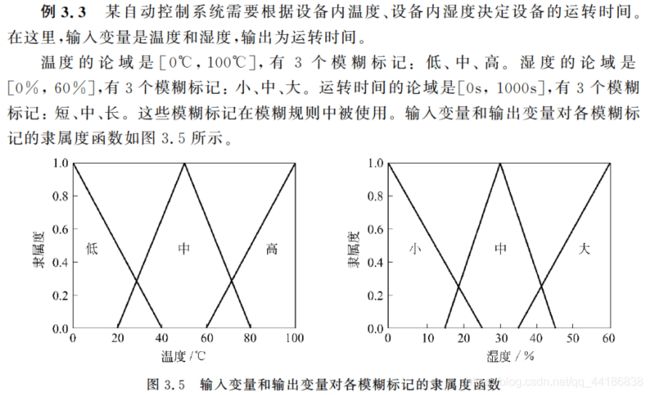
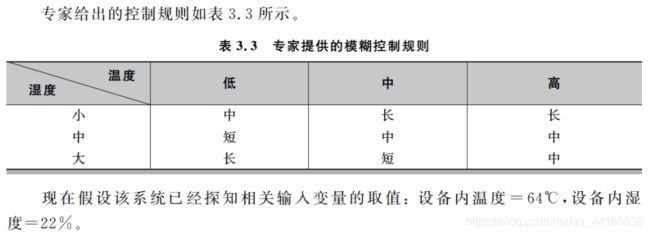
计算输出过程如下:
(1) 输入变量模糊化并激活相应规则
输入变量模糊化,得到隶属度如表:
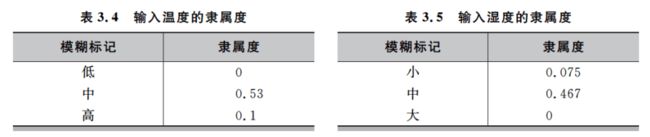
由于温度对“低”的隶属度为0,而湿度对“大”的隶属度为0,故控制规则表内条件包含低温度和大湿度的规则不被激活。而有如下4条规则被激活:
a. 若温度为高且湿度为小,则运转时间为长。
b. 若温度为中且湿度为中,则运转时间为中。
c. 若温度为中且湿度为小,则运转时间为长。
d. 若温度为高且湿度为中,则运转时间为中。
(2) 计算模糊控制规则的强度
这一步骤属于“推理方法”模块。采用不同的推理方法,(2)的具体步骤也不相同。
由于规则条件中连接两个条件的是“且”,故在此选用取最小值法确定四条规则的强度:
规则a:温度对“高”隶书度为0.1,湿度对“小”隶属度为0.075,min(0.1, 0.075)=0.075
规则b:温度对“中”隶书度为0.53,湿度对“中”隶属度为0.467,min(0.53, 0.467)=0.467
规则c:温度对“中”隶书度为0.53,湿度对“小”隶属度为0.075,min(0.53,0.075)=0.075
规则d:温度对“高”隶书度为0.1,湿度对“中”隶属度为0.467,min(0.1,0.467)=0.1
(3)确定模糊输出并去模糊化
这一步骤属于“推理方法”和“去模糊化”模块。采用不同的推理方法,(3)的具体步骤也不相同。
规则a和规则c的结论是运转时间为长,规则b和规则d的结论是运转时间为中。故运转时间对“长”的隶属度是规则a和规则c强度较大者0.075,运转时间对“中”的隶属度是规则b和规则d强度较大者0.467。
进行去模糊化,最终的输出为:
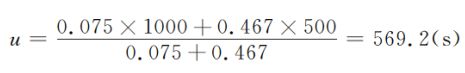
总结一下,其实我们不难发现,上述实现过程非常简单。尽管现实生活中的实例要更复杂得多,但是只要我们掌握了模糊逻辑的思想,一切都会慢慢变得简单的!
3.5 模糊逻辑的应用
模糊计算适用于:
(1)复杂且没有完整数学模型的非线性问题
可在不知晓具体模型的情况下利用经验规则求解。
(2)与其它智能算法结合实现优势互补
提供了将人类在识别、决策、理解等方面的模糊性引入机器及其控制的途径 。
模糊系统与神经网络
模糊系统适合于描述自然语言与人类思维中的模糊性,而神经网络具有学习、联想、记忆的能力。模糊系统与神经网络结合,实现了优势互补。
模糊逻辑与进化计算
(1)在进化计算算法运行时使用模糊控制来调整群智能算法的参数。
(2)在模糊系统中用进化计算算法来产生、挑选和优化模糊控制规则与隶属度函数。
第4章 遗传算法
4.1 遗传算法简介
4.1.1 基本原理
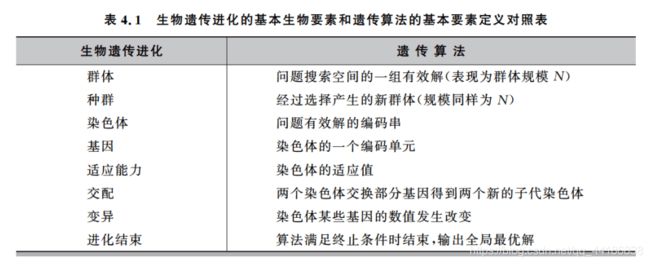
同第二章神经网络一样,这一章开头也提到了很多生物学的知识。
遗传算法(Genetic Algorithm,GA)是进化计算的一个分支,是一种模拟自然界生物进化过程的随机搜索算法。
GA思想源于自然界“自然选择”和“优胜劣汰”的进化规律,通过模拟生物进化中的自然选择和交配变异寻找问题的全局最优解。它最早由美国密歇根大学教授John H. Holland提出,现在已经广泛应用于各种工程领域的优化问题之中。
遗传算法通过比较适应值区分染色体的优劣,适应值越大的染色体越优秀。评估函数涌过来计算染色体对应的适应值。
选择算子按一定的规则对群体的染色体进行选择,得到父代种群。(一般的,越优秀的染色体被选中的次数越多。)
交配算子作用于每两个成功交配的染色体,染色体交换各自部分的基因,形成两个子代染色体。子代染色体取代父代进入新种群,而没有交配的染色体自动进入新的种群。
变异算子使得新种群进行小概率的变异。染色体发生变异的基因改变数值,经过变异的新种群替代原种群进入下一次进化。

Holland的模式定理提出,遗传算法的实质是通过选择、交配和变异算子对模式进行搜索,低阶、定义长度较小且平均适应值高于群体平均适应值的模式在群体中的比例将呈指数级增长。即随着进化的不断进行,较优染色体的个数将快速增加。
积木块假设
积木块:指低阶、定义长度较小且平均适应值高于群体平均适应值的模式 。
积木块假设认为在遗传算法运行过程中,积木块在遗传算子的影响下能够相互结合,产生新的更加优秀的积木块,最终接近全局最优解 。
4.1.2 研究进展
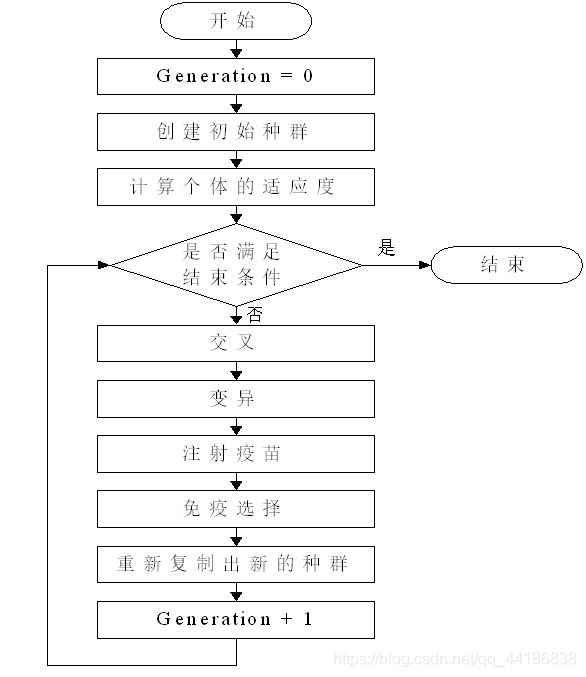
4.2 遗传算法的流程
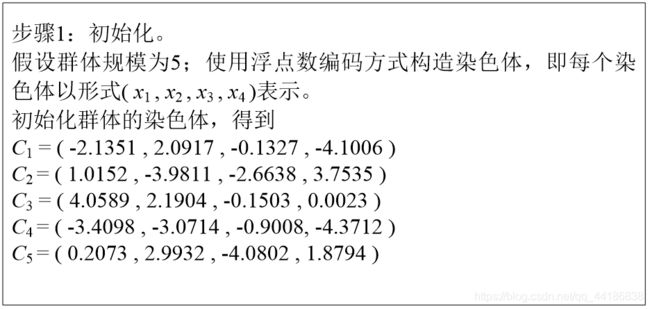
(1)染色体编码
目前用于染色体编码的方法有格雷码编码、字母编码、多参数交叉编码等。这里仅给出两种常见的较为简单的编码方法:二进制编码方法和浮点数编码方法。
二进制编码方法

![]()
二进制编码操作简单,但当你的L较大时,计算难度会增大,难以解决精度要求高的问题,因此,我们需要寻求另外的编码方法。
一般情况下,遗传算法在群体初始化阶段采用的是随机数初始化方法。采用生成随机数的方法,对染色体的每一维变量进行初始化赋值。初始化染色体时必须注意染色体是否满足优化问题对有效解的定义。
如果在进化开始时保证初始群体已经是一定程度上的优良群体的话,将能够有效提高算法找到全局最优解的能力。
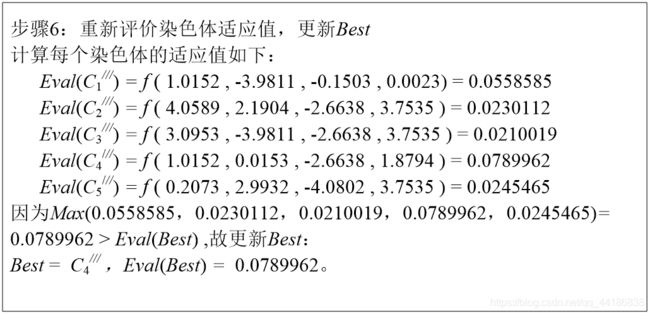
(3)适应值评价
评估函数用于评估各个染色体的适应值,进而区分优劣。评估函数常常根据问题的优化目标来确定,比如在求解函数优化问题时,问题定义的目标函数可以作为评估函数的原型。
在遗传算法中,规定适应值越大的染色体越优。因此对于一些求解最大值的数值优化问题,我们可以直接套用问题定义的函数表达式。但是对于其他优化问题,问题定义的目标函数表达式必须经过一定的变换。
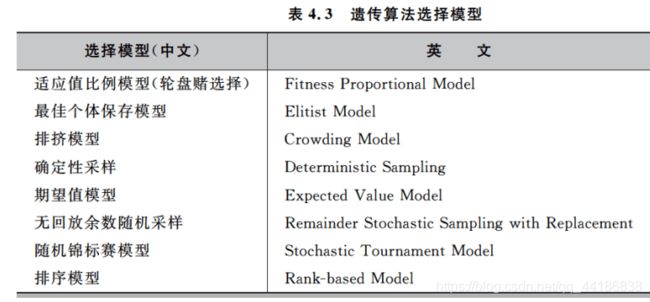
(4)选择算子
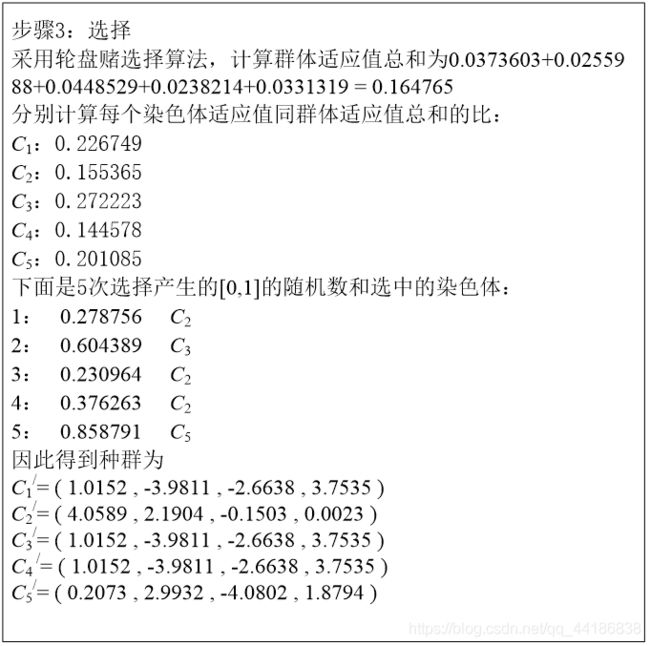
轮盘赌选择法
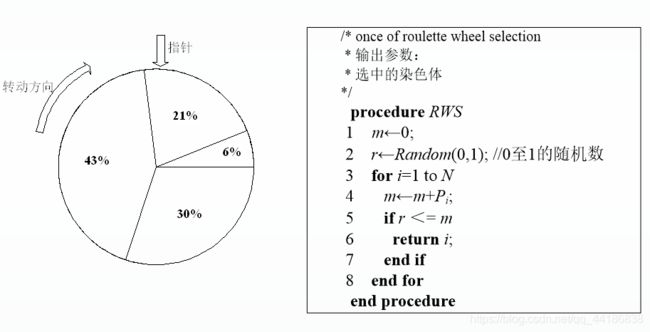
按适应值大小切分区域大小,即适应值越大的染色体占比越大,越有可能被选中,同时由于是随机选取,也保证了适应值小的染色体也有被选中的可能。
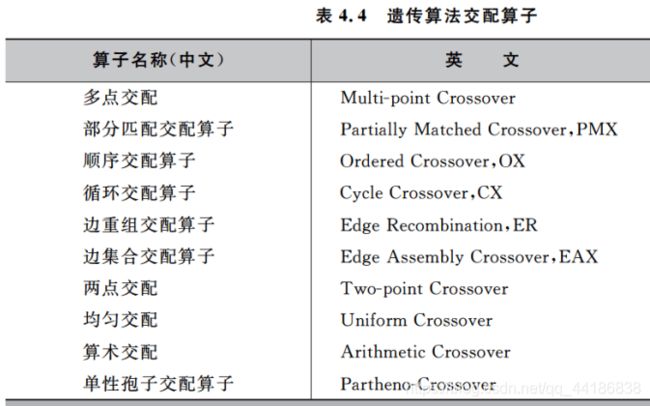
(5)交配算子
在染色体交配阶段,每个染色体能否进行交配由交配概率Pc(一般取值为0.4到0.99之间)决定,其具体过程为:对于每个染色体,如果Random(0, 1)小于Pc则表示该染色体可进行交配操作(其中Random(0, 1)为[0, 1]间均匀分布的随机数),否则染色体不参与交配直接复制到新种群中。
每两个按照Pc交配概率选择出来的染色体进行交配,经过交换各自的部分基因,产生两个新的子代染色体。具体操作是随机产生一个有效的交配位置,染色体交换位于该交配位置后的所有基因。
注意:因为父代是两个染色体,生成的子代也是两个染色体,故种群染色体总数N值不会改变。
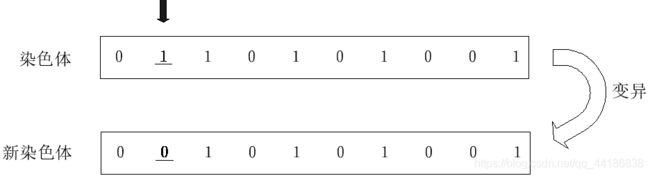
(6)变异算子
染色体的变异作用于基因之上,对于交配后新种群中染色体的每一位基因,根据变异概率Pm判断该基因是否进行变异。
如果Random(0, 1)小于Pm,则改变该基因的取值(其中Random(0, 1)为[0, 1]间均匀分布的随机数)。否则该基因不发生变异,保持不变。
够简单理解吧。
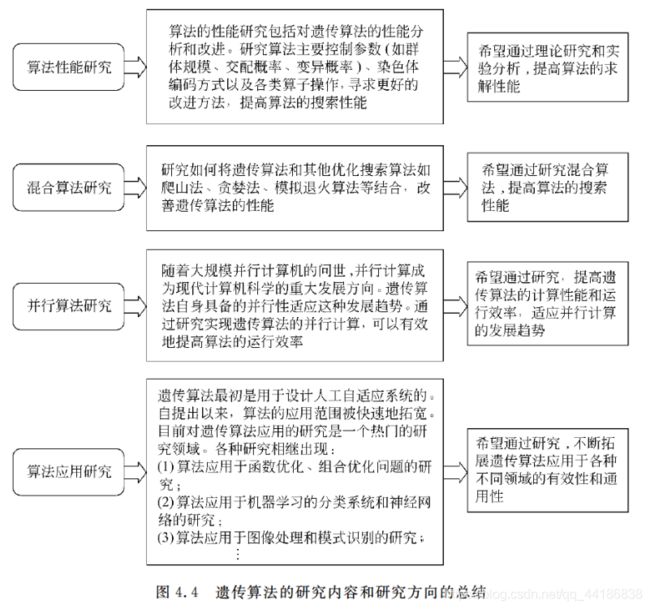
4.3 遗传算法的改进
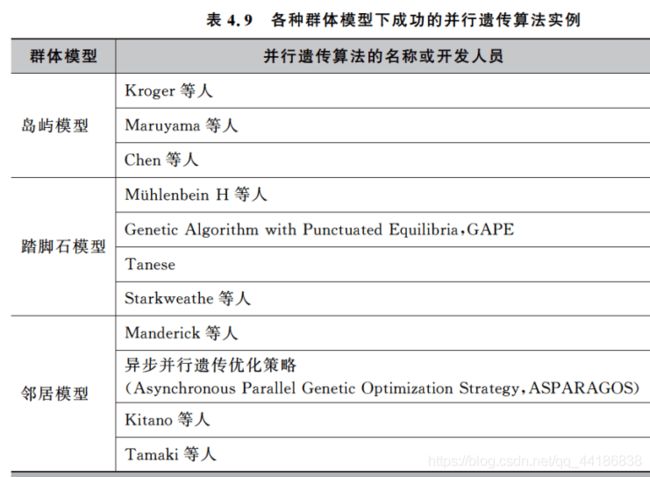
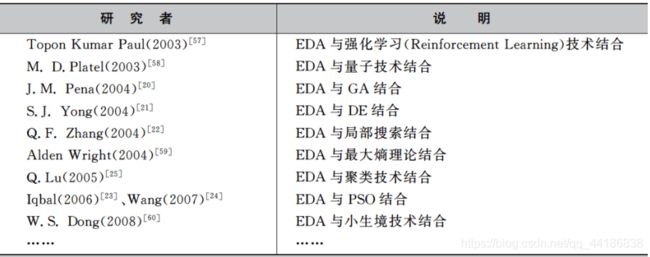
没有完美的算法,只有适合的算法。下文会贴出每种问题对应的多种研究,感兴趣的可以自行上网查看。
4.3.1 算子选择
4.3.2 参数设置
群体规模N
影响算法的搜索能力和运行效率。
若N设置较大,一次进化所覆盖的模式较多,可以保证群体的多样性,从而提高算法的搜索能力,但是由于群体中染色体的个数较多,势必增加算法的计算量,降低了算法的运行效率。
若N设置较小,虽然降低了计算量,但是同时降低了每次进化中群体包含更多较好染色体的能力。
N的设置一般为20~100。
染色体长度L
影响算法的计算量和交配变异操作的效果。
L的设置跟优化问题密切相关,一般由问题定义的解的形式和选择的编码方法决定。
对于二进制编码方法,染色体的长度L根据解的取值范围和规定精度要求选择大小。
对于浮点数编码方法,染色体的长度L 跟问题定义的解的维数D相同。
除了染色体长度一定的编码方法,Goldberg等人还提出了一种变长度染色体遗传算法Messy GA,其染色体的长度并不是固定的。
基因取值范围R
R视采用的染色体编码方案而定。
对于二进制编码方法,R ={0,1},而对于浮点数编码方法,R与优化问题定义的解每一维变量的取值范围相同。
交配概率Pc
决定了进化过程种群参加交配的染色体平均数目。
取值一般为0.4至0.99。也可采用自适应方法调整算法运行过程中的交配概率。
变异概率Pm
增加群体进化的多样性,决定了进化过程中群体发生变异的基因平均个数。
Pm的值不宜过大。因为变异对已找到的较优解具有一定的破坏作用,如果Pm的值太大,可能会导致算法目前处于的较好的搜索状态倒退回原来较差的情况。
Pm的取值一般为0.001至0.1之间。也可采用自适应方法调整算法运行过程中的Pm值。
适应值评价
影响算法对种群的选择,恰当的评估函数应该能够对染色体的优劣做出合适的区分,保证选择机制的有效性,从而提高群体的进化能力。
评估函数的设置同优化问题的求解目标有关。
评估函数应满足较优染色体的适应值较大的规定。
为了更好地提高选择的效能,可以对评估函数做出一定的修正。
目前主要的评估函数修正方法有:线性变换;乘幂变换;指数变换等。
终止条件
决定算法何时停止运行,输出找到的最优解,采用何种终止条件,跟具体问题的应用有关。
可以使算法在达到最大进化代数时停止,最大进化代数一般可设置为100~1000,根据具体问题可对该建议值作相应的修改。
也可以通过考察找到的当前最优解是否达到误差要求来控制算法的停止。
或者是算法在持续很长的一段进化时间内所找到的最优解没有得到改善时,算法可以停止。
4.3.3 混合遗传算法
提出混合遗传算法的原因有两个,一是遗传算法存在局部搜索能力较弱的缺陷,二是当遗传算法应用到专门的领域时往往不是最佳的方法。
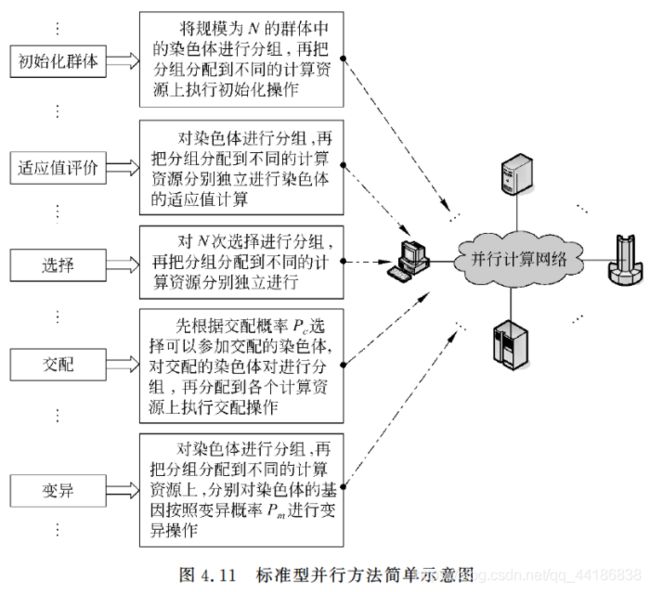
4.3.4 并行遗传算法
并行计算
单指令流多数据流计算机
多指令流多数据流计算机
并行计算网络
串行计算
单指令流单数据流处理器
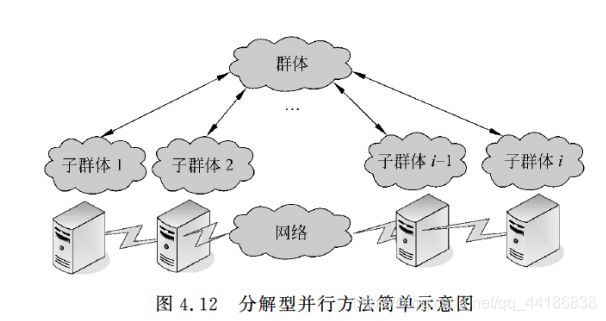
并行遗传算法一般有两种表现形式:标准型并行方法和分解型并行方法。
4.4 遗传算法的应用
第5章 蚁群优化算法
每看一章,我都会感觉这些数学家们怎么都这么聪明,有句话叫“艺术源于生活”,我想,其实数学也来源于生活。
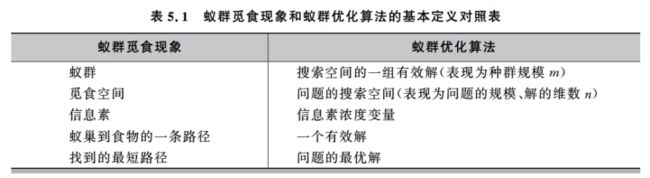
5.1 基本原理
先来聊下该算法的思想来源:
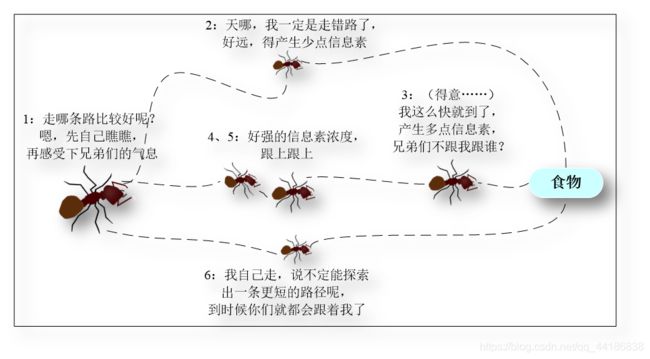
自然界蚂蚁群体在寻找食物的过程中,通过一种被称为信息素(Pheromone)的物质实现相互的间接通信,从而能够合作发现从蚁穴到食物源的最短路径。
通过对这种群体智能行为的抽象建模,研究者提出了蚁群优化算法(Ant Colony Optimization, ACO),为最优化问题、尤其是组合优化问题的求解提供了一强有力的手段。
蚂蚁在寻找食物的过程中往往是随机选择路径的,但它们能感知当前地面上的信息素浓度,并倾向于往信息素浓度高的方向行进。信息素由蚂蚁自身释放,是实现蚁群内间接通信的物质。由于较短路径上蚂蚁的往返时间比较短,单位时间内经过该路径的蚂蚁多,所以信息素的积累速度比较长路径快。因此,当后续蚂蚁在路口时,就能感知先前蚂蚁留下的信息,并倾向于选择一条较短的路径前行。这种正反馈机制使得越来越多的蚂蚁在巢穴与食物之间的最短路径上行进。由于其他路径上的信息素会随着时间蒸发,最终所有的蚂蚁都在最优路径上行进。
5.2 算法流程
下面以求解TSP(旅行商问题)为例,来描述蚁群优化算法的工作机制。
5.2.1 基本流程
蚂蚁系统(Ant System,AS)是最基本的ACO算法,是以TSP作为应用实例提出的。
AS对于TSP的求解流程大致可分为两部:路径构建和信息素更新。
(1)路径构建
伪随机比例选择规则(random proportional)。
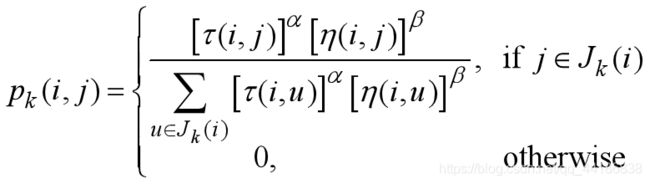
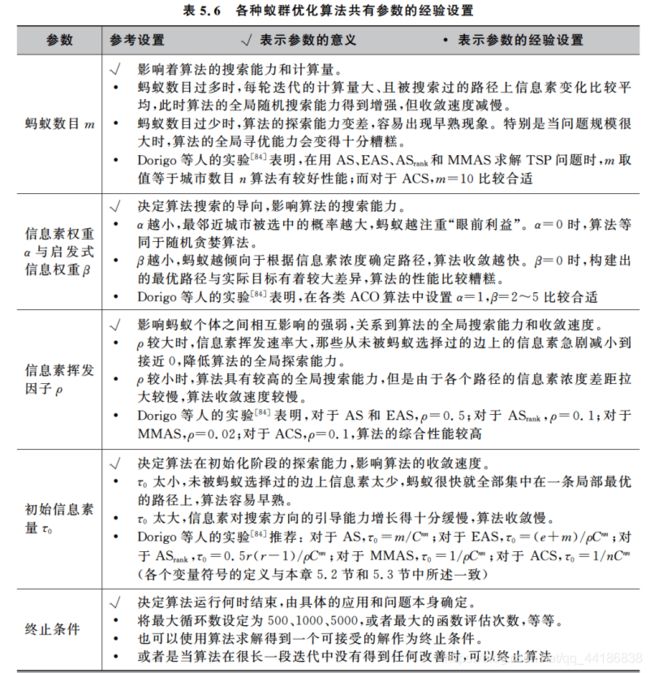
对于每只蚂蚁k,路径记忆向量 R k R^k Rk按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i,则其选择城市j作为下一个访问对象的概率如上式。 J k J_k Jk(i)表示从城市i可以直接到达的、且又不在蚂蚁访问过的城市序列 R k R^k Rk中的城市集合。 η \eta η(i, j)是一个启发式信息,通常由 η \eta η (i, j)=1/ d i j d_ij dij直接计算。 τ \tau τ(i, j)表示边(i, j)上的信息素量。
长度越短、信息素浓度越大的路径被蚂蚁选择的概率越大。a和b是两个预先设置的参数,用来控制启发式信息与信息素浓度作用的权重关系。当a=0时,算法演变成传统的随机贪心算法,最邻近城市被选中的概率最大。当b=0时,蚂蚁完全只根据信息素浓度确定路径,算法将快速收敛,这样构建出的最优路径往往与实际目标有着较大的差异,算法的性能比较糟糕。
(2)信息素更新
- 在算法初始化时,问题空间中所有的边上的信息素都被初始化为t0。
- 算法迭代每一轮,问题空间中的所有路径上的信息素都会发生蒸发,我们为所有边上的信息素乘上一个小于1的常数。信息素蒸发是自然界本身固有的特征,在算法中能够帮助避免信息素的无限积累,使得算法可以快速丢弃之前构建过的较差的路径。
- 蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素。蚂蚁构建的路径越短、释放的信息素就越多。一条边被蚂蚁爬过的次数越多、它所获得的信息素也越多。
- 迭代(2),直至算法终止。
看不懂?那结合下面公式来看。
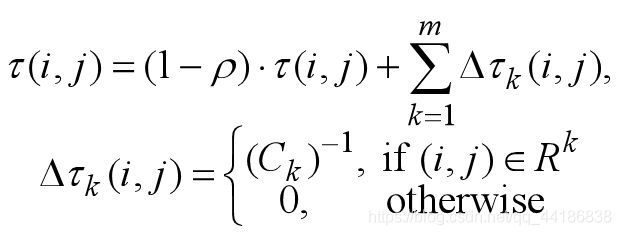
m是蚂蚁个数;r是信息素的蒸发率,规定0
5.2.2 应用举例
接着,我们结合一个实例来做进一步理解。
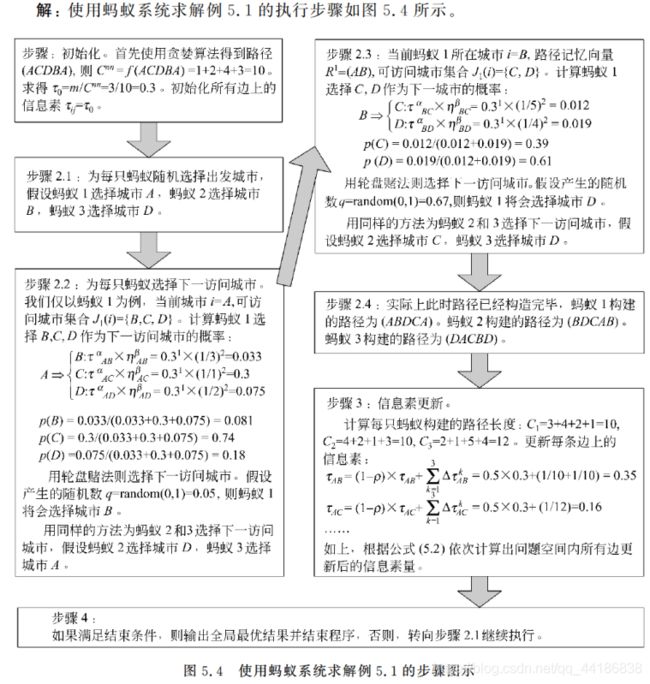
步骤2.2中有提到轮盘赌法。是的,和我们遗传算法用的是一样的(当然后面新的方法会有不一样)。
轮盘赌法具体怎么操作,我这里稍微解释一下:
比方说,现在A占比为0.2,B占比为0.5,C占比为0.3。
则当你随机值大小位于为0-0.2时,选A,大小位于0.2-0.7时,选B,大小位于0.7-1.0时,选C。
5.3 改进版本
5.3.1 精华蚂蚁系统
精华蚂蚁系统(Elitist Ant System,EAS)是对基础AS的第一次改进,它在原AS信息素更新原则的基础上增加了一个对至今最优路径的强化手段。
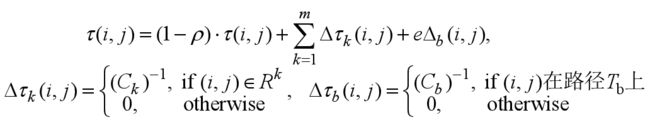
引入这种额外的信息素强化手段有助于更好地引导蚂蚁搜索的偏向,使算法更快收敛。
5.3.2 基于排列的蚂蚁系统
基于排列的蚂蚁系统(rank-based Ant System, A S r AS_r ASr a _a a n _n n k _k k)在AS的基础上给蚂蚁要释放的信息素大小加上一个权值,进一步加大各边信息素量的差异,以指导搜索。在每一轮所有蚂蚁构建完路径后,它们将按照所得路径的长短进行排名,只有生成了至今最优路径的蚂蚁和排名在前( ω \omega ω-1)的蚂蚁才被允许释放信息素,蚂蚁在边(i, j)上释放的信息素 的权值由蚂蚁的排名决定。
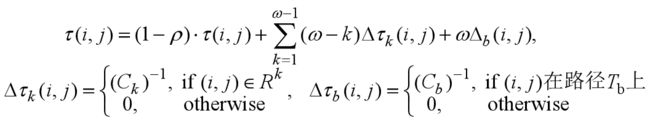
权值( ω \omega ω−k)对不同路径的信息素浓度差异起到了一个放大的作用, A S r AS_r ASr a _a a n _n n k _k k能更有力度地指导蚂蚁搜索。
5.3.3 最大最小蚂蚁系统
最大最小蚂蚁系统(MAX-MIN Ant System,MMAS)在基本AS算法的基础上进行了四项改进:
(1)只允许迭代最优蚂蚁(在本次迭代构建出最短路径的蚂蚁),或者至今最优蚂蚁释放信息素。(迭代最优更新规则和至今最优更新规则在MMAS中会被交替使用。)
如果只使用至今最优更新规则进行信息素的更新,搜索的导向性很强,算法会很快收敛到 T b T_b Tb附近;反之,如果只使用迭代最优更新规则,则算法的探索能力会得到增强,但收敛速度会下降。实验结果表明,对于小规模的TSP问题,仅仅使用迭代最优信息素更新方式即可。随着问题规模的增大,至今最优信息素规则的使用变得越来越重要。
(2)信息素量大小的取值范围被限制在一个区间[ τ m \tau_m τm i _i i n _n n, τ m \tau_m τm a _a a x _x x]内。
当信息素浓度也被限制在一个范围内以后,位于城市i的蚂蚁k选择城市j作为下一城市的概率也将被限制在一个区间内。算法有效避免了陷入停滞状态(所有蚂蚁不断重复搜索同一条路径)的可能性。
(3)信息素初始值为信息素取值区间的上限,并伴随一个较小的信息素蒸发速率。
利好:增强算法在初始阶段的探索能力,有助于蚂蚁“视野开阔地”进行全局范围内的搜索。
随后蚂蚁逐渐缩小搜索范围。
(4)每当系统进入停滞状态,问题空间内所有边上的信息素量都会被重新初始化。(我们通常通过对各条边上信息素量大小的统计或是观察算法在指定次数的迭代内至今最优路径有无被更新来判断算法是否停滞。)
有效地利用系统进入停滞状态后的迭代周期继续进行搜索,使算法具有更强的全局寻优能力。
5.3.4 蚁群系统
1997年,蚁群算法的创始人Dorigo在“Ant colony system: a cooperative learning approach to the traveling salesman problem”一文中提出了一种具有全新机制的ACO算法——蚁群系统(Ant Colony System,ACS),进一步提高了ACO算法的性能。
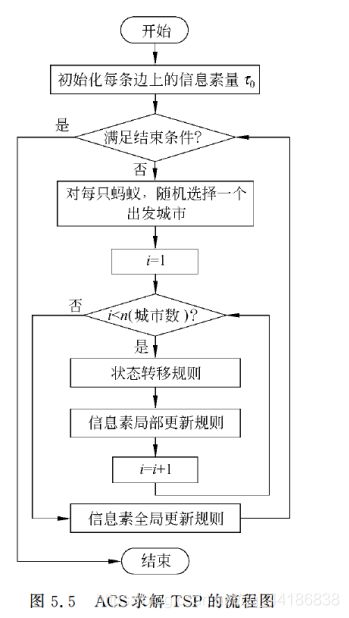
(1)使用一种伪随机比例规则(pseudorandom proportional)选择下城市节点,建立开发当前路径与探索新路径之间的平衡。
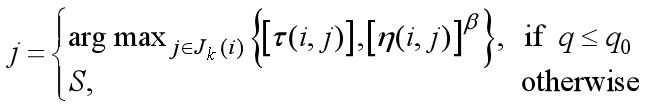
(1)使用一种伪随机比例规则(pseudorandom proportional)选择下城市节点,建立开发当前路径与探索新路径之间的平衡。
q0是一个[0, 1]区间内的参数,当产生的随机数q≤q0时,蚂蚁直接选择使启发式信息与信息素量的指数乘积最大的下城市节点,我们通常称之为开发(exploitation);反之,当产生的随机数q>q0时ACS将和各种AS算法一样使用轮盘赌选择策略,我们称之为偏向探索(bias exploration)。
通过调整q0,我们能有效调节“开发”与“探索”之间的平衡,以决定算法是集中开发最优路径附近的区域,还是探索其它的区域。
(2)使用信息素全局更新规则,每轮迭代中所有蚂蚁都已构建完路径后,在属于至今最优路径的边上蒸发和释放信息素。
![]()
其中 Δ \Delta Δ τ b \tau_b τb(i, j) = 1 / C b C_b Cb,不论是信息素的蒸发还是释放,都只在属于至今最优路径的边上进行,这里与AS有很大的区别。因为AS算法将信息素的更新应用到了系统的所有边上,信息素更新的计算复杂度为O( n 2 n^2 n2),而ACS算法的信息素更新计算复杂度降低为O(n)。参数 ρ \rho ρ代表信息素蒸发的速率,新增加的信息素 被乘上系数 ρ \rho ρ后,更新后的信息素浓度被控制在旧信息素量与新释放的信息素量之间,用一种隐含的又更简单的方式实现了MMAS算法中对信息素量取值范围的限制。
(3)引入信息素局部更新规则,在路径构建过程中,对每一只蚂蚁,每当其经过一条边(i, j)时,它将立刻对这条边进行信息素的更新。
![]()

信息素局部更新规则作用于某条边上会使得这条边被其他蚂蚁选中的概率减少。这种机制大大增加了算法的探索能力,后续蚂蚁倾向于探索未被使用过的边,有效地避免了算法进入停滞状态。
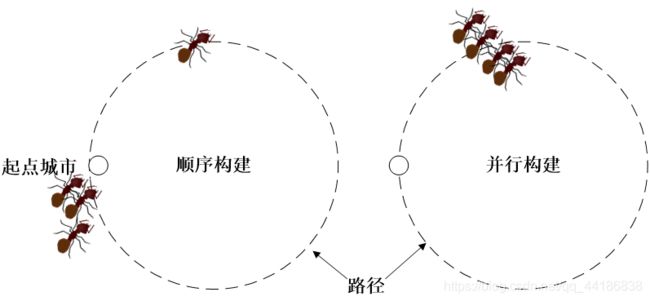
顺序构建和并行构建。顺序构建是指当一只蚂蚁完成一轮完整的构建并返回到初始城市之后,下一只蚂蚁才开始构建;并行构建是指所有蚂蚁同时开始构建,每次所有蚂蚁各走一步(从当前城市移动到下一个城市)。对于ACS,要注意到两种路径构建方式会造成算法行为的区别。
在ACS中通常我们选择让所有蚂蚁并行地工作。
5.3.5 连续正交蚁群系统
连续正交蚁群算法(Continuous Orthogonal Ant Colony, COAC):近年来,将应用领域扩展到连续空间的蚁群算法也在发展,连续正交蚁群就是其中比较优秀的一种。COAC通过在问题空间内自适应地选择和调整一定数量的区域,并利用蚂蚁在这些区域内进行正交搜索、在区域间进行状态转移、并更新各个区域的信息素来搜索问题空间中的最优解。
COAC的基本思想是利用正交试验的方法将连续空间离散化。
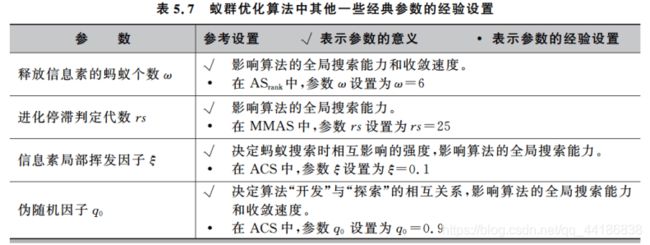
5.4 参数设置
第6章 粒子群优化算法
6.1 粒子群优化算法简介
粒子群优化算法(Particle Swarm Optimization,PSO)是进化计算的一个分支,是一种模拟自然界的生物活动的随机搜索算法。
PSO模拟了自然界鸟群捕食和鱼群捕食的过程。通过群体中的协作寻找到问题的全局最优解。它是1995年由美国学者Eberhart和Kennedy提出的,现在已经广泛应用于各种工程领域的优化问题之中。
6.1.1 思想来源
从动物界中的鸟群、兽群和鱼群等的迁移等群体活动而来。在群体活动中,群体中的每一个个体都会受益于所有成员在这个过程中所发现和累积的经验。
6.1.2 基本原理
在粒子群优化算法中,鸟群中的每个小鸟被称为“粒子”,且同小鸟一样,具有速度和位置。
通过随机产生一定数量的粒子(具体定多少数量后面会讲)作为问题搜索空间的有效解,然后进行迭代搜索,通过该问题对应的适应度函数确定粒子的适应值,得到优化结果。
那具体怎么迭代搜索呢?后面实例会具体讲到。
且这里记得有所谓的“粒子本身的历史最优解”和“群体的全局最优解”,这两个用来影响粒子的速度和下一个位置,借此求得最优解。
6.2.1 基本流程
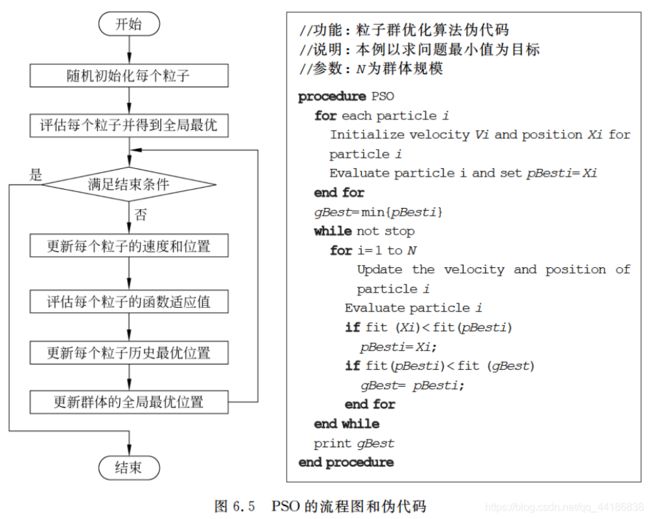
来看一下PSO的算法步骤:
(1)初始化所有粒子,即给它们的速度和位置赋值,并将个体的历史最优pBest设为当前位置,群体中的最优个体作为当前的gBest。
(2)在每一代的进化中,计算各个粒子的适应度函数值。
(3)如果当前适应度函数值优于历史最优值,则更新pBest。
(4)如果当前适应度函数值优于全局历史最优值,则更新gBest。
(5)对每个粒子i的第d维的速度和位置分别按照公式6.1和公式6.2进行更新:
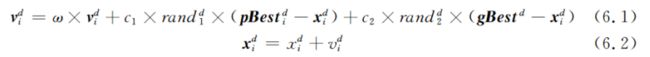

(6)判断是否达到了结束条件(具体怎么定义后面会提),否的话就转到(2)继续执行。
算法流程图和伪代码
6.2.2 应用举例
上面看不懂?
没关系,看了这个实例,保证你能理解最简单的PSO是如何实现的。
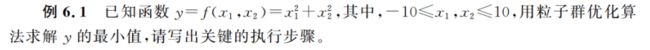

注意对于越界的位置,需要进行合法性调整,将超出定义范围的数值改成范围内的边界值。
6.3 粒子群优化算法的改进研究
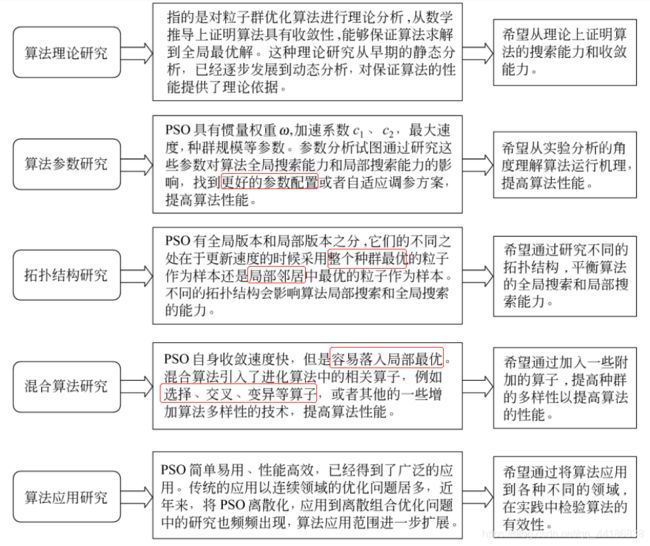
粒子群优化算法的研究内容和改进方向
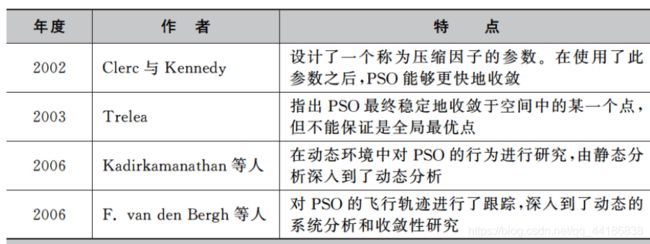
6.3.1 理论研究改进
年代久远,看看就成了。
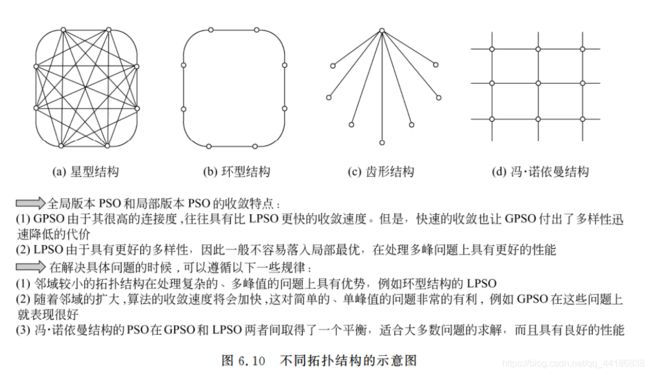
6.3.2 拓扑结构改进
1.静态拓扑结构‘’
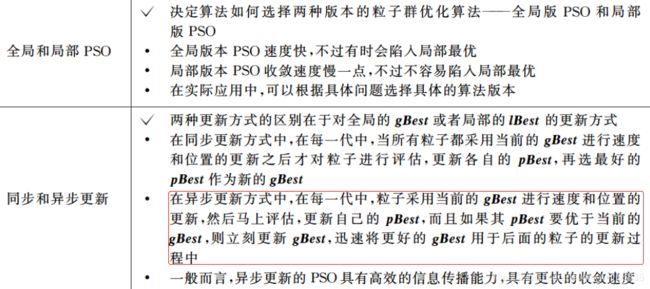
全局版本(Global Version PSO, GPSO)和局部版本(Local Version PSO, LPSO)两个主要范式。
两者主要区别在于社会网络结构的定义不同。
从全局和局部其实也不难看出,粒子在更新速度和位置的时候,前者使用到的是自身的历史最好位置pBest和整个群体中最好的位置gBest,而后者的话,每个粒子所处的“社会”不是整体,而是一个小的邻域。更新速度和位置时用到的除了自身最好的历史位置pBest外,还用到邻域中的最好位置lBest作为更新的向导。
不难发现,后者的多样性更好,在处理复杂的问题的时候,LPSO也会表现出更好的性能。
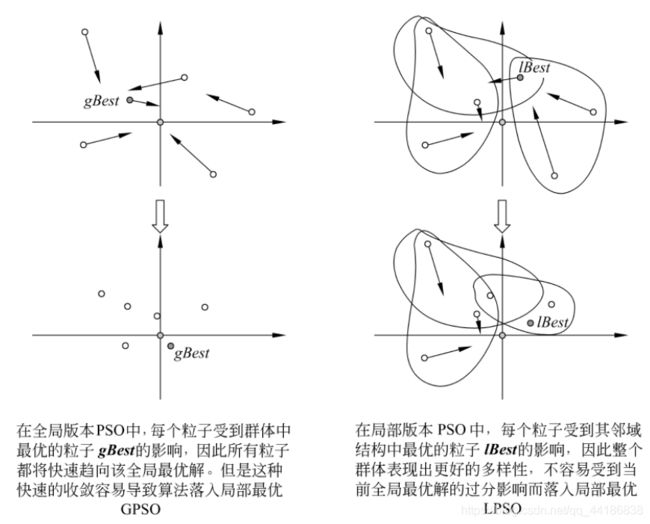
2.动态拓扑结构
由于即使是LPSO也很容易陷入局部最优的问题,而研究动态拓扑结构是希望能够通过在不同的进化阶段使用不同的拓扑结构,动态地改变算法的探索能力和开发能力,在保种群多样性和算法收敛性上取得动态的变化和平衡,以提高算法的整体性能。
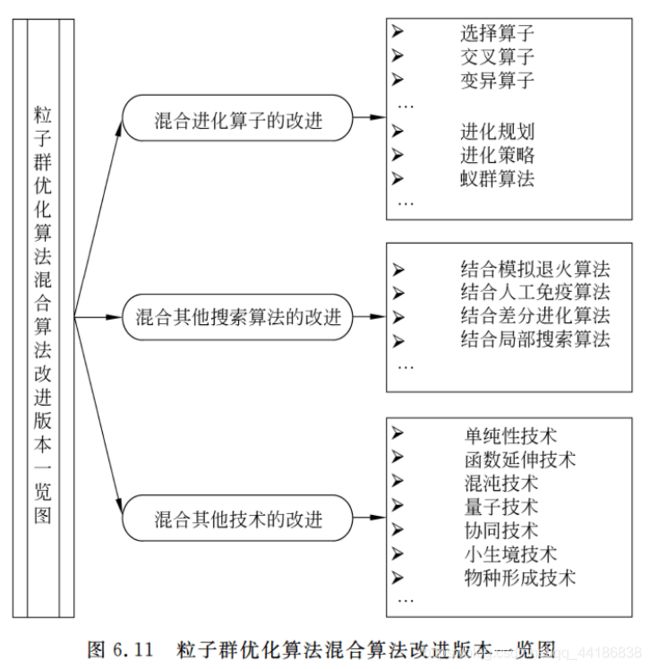
6.3.3 混合算法改进
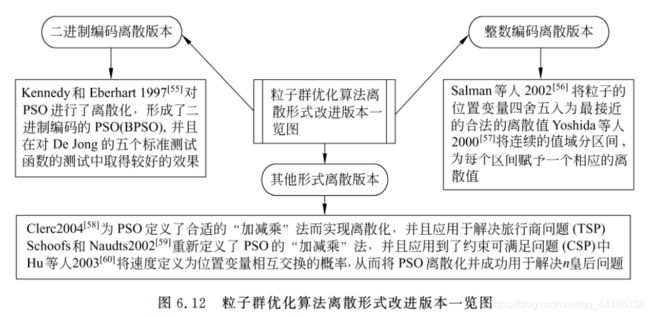
6.3.4 离散版本改进
PSO是非常适合于连续领域问题优化的算法,且已经在此取得相当成功的应用。
离散版本改进将PSO运用到离散领域(组合优化)之中。
在众多的离散PSO改进版本中,二进制编码PSO和整数编码PSO是常见的两种形式。
6.4 相关应用
6.5 参数设置
第7章 免疫算法
说实话,连续几天啃这本书,我有了些许疲惫。然后到了这一章,发现难度稍微大了一点,而且最可惜的是它竟然没有应用实例???
不过无所谓,没有就我自己网上搜呗。
然后这一章我照样会放公式上来,不过也希望大家在弄懂公式的同时,更加注重算法的实现思想,掌握了所谓的底层思想,算法自然也不会那么难了。
7.1 算法简介
免疫算法(Immune Algorithm,IA):是指以在人工免疫系统的理论为基础,实现了类似于生物免疫系统的抗原识别、细胞分化、记忆和自我调节的功能的一类算法。
引用目前百度对其的定义:

有没有看到这里好奇了的小伙伴?为啥遗传算法和免疫算法扯上了关系?
但其实学完免疫算法你会发现,两者其实非常的相似。
遗传算法的思想简单讲就是父代之间通过交叉互换以及变异产生子代,不断更新适应度更高的子代,从而达到优化的效果。
而免疫算法本质上其实也是更新亲和度(这里对应上面的适应度)的过程,抽取一个抗原(问题),取一个抗体(解)去解决,并计算其亲和度,而后选择样本进行变换操作(免疫处理),借此得到得分更高的解样本,在一次一次的变换过程中逐渐接近最后解。
7.1.1 思想来源
免疫算法最先起源于1973-1976年间Jernel的三篇关于免疫网络的文章,Jernel在文中提出了一组基于免疫独特型的微分方程,这就是最早的免疫系统。
免疫算法的主要会议:
International Conference on Artificial Immune Systems,ICARIS
7.1.2 免疫算法的生物模型
先来看一下人体免疫系统大致是怎么工作的:
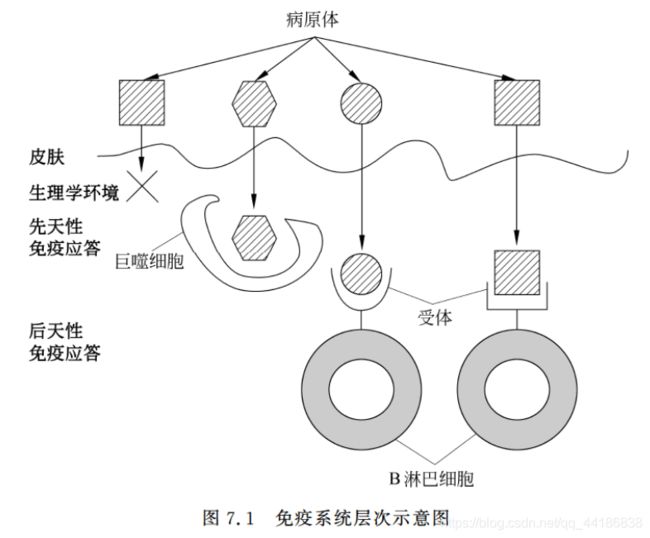
具体我就不多讲了好吧,大家可能懂得比我还多,毕竟我高中毕业已经很久了害。
7.1.3 二进制模型
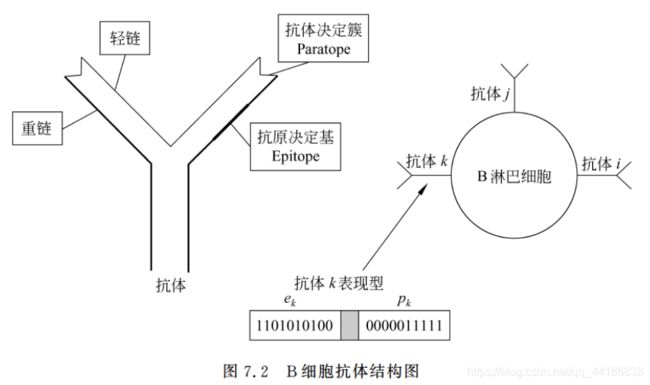
Farmer用二进制串表示那些描述了抗体决定簇和抗原决定基性质的氨基酸序列,然后假设每个抗原和每个康提醒分别只有一个抗原决定簇(实际都有很多)。通过这些决定基之间的匹配程度不同类型抗体的复制和减少,以达到优化系统的目的。
二进制模型模仿了免疫系统的工作原理,主要涉及识别和刺激两方面的内容。
那我这里简单讲下它的实现思想。
首先是识别:通过该环节得到两者之间的匹配度,为后面刺激新抗体的生成做准备。
刺激:生成更多亲和度高的抗体,抑制其他弱抗体的生成。
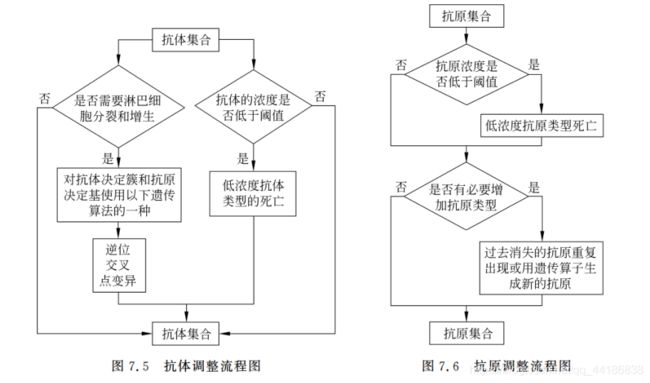
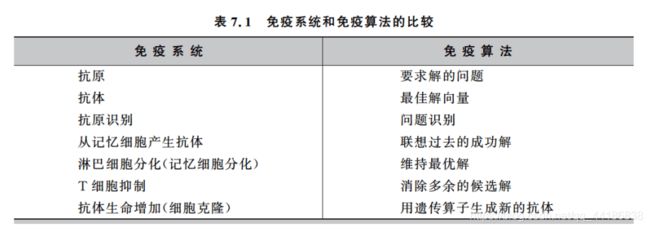
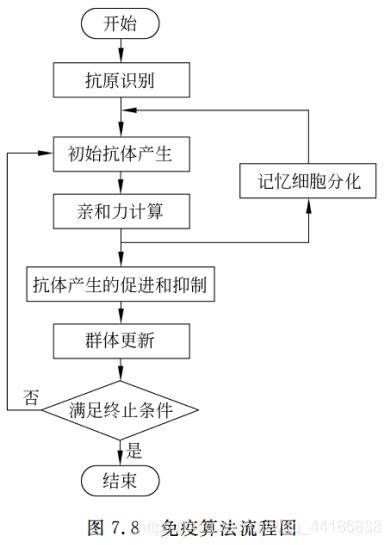
7.2 免疫算法的基本流程
7.2.1 基本流程
识别抗体,生成初始化的抗体,计算亲和度,记忆细胞分化,抗体促进和抑制,产生新的抗体,结束条件。
(1)识别抗体
把目标函数和约束作为抗体。
(2)生成初始化的抗体
随机生成独特型串维数为M的N个抗体。
(3)计算亲和度
这个步骤可以说是免疫算法的重点,同时也是最难点。


如果看到这遇到了问题,请放心,这些是正常情况,可以的话,大家阔以去参考一些实例问题,通过对实例的具体解决过程来读懂这些公式或许会更简单一些。
那这里我就稍微贴一下我觉得比较不错的推荐:https://www.bilibili.com/video/BV1pV411C7Sx?p=4
这里可能也需要大家有一定的matlab基础。
(4)记忆细胞分化
同人的免疫系统基本一致。
与抗原有最大亲和度的抗体加入了记忆细胞。由于记忆细胞数目有限,因此新生成的抗体将会代替记忆细胞中和它有最大亲和力者。
(5)抗体促进和抑制
最开始我介绍免疫算法其实就有提到这个。
通过计算抗体v的期望值,消除那些低期望值的抗体。
抗体v的期望值 e v e_v ev的计算公式为:
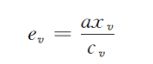
其中抗体v的密度的计算方法如下:
![]()
其中 q k q_k qk表示和抗体k有较大亲和力的抗体。通过这个公式能有效地抑制抗体的过分相似,避免算法的未成熟收敛。
(6)产生新的抗体
这里就对应我最开始提到的遗传算法和免疫算法相似地方了。
基于不同抗体和抗原亲和力的高低,使用轮盘赌的方法 ,选择两个抗体。然后把这两个抗体按一定变异概率做变异,之后再做交叉,得到新的抗体。重复操作(6)知道产生所有N个新抗体。可以说免疫算法产生新的抗体的过程需要遗传算子的辅助。
(7)结束条件
如果求出的最优解满足一定的结束条件,则结束算法。
7.2.2 更一般的基本免疫算法
1.求解多目标优化问题的免疫算法
先前我们提出的基本流程其实用于解决的知识单目标的优化问题,那如果是多目标呢?
思考一下,一个目标即一个问题,一个问题对应免疫算法其实就是一个抗原。
所以求解多目标优化问题,抗原将抗原从原先的一个扩展到L个,这个L的值即等于你一共目标的值。同时,抗原v和抗原 ω \omega ω的亲和度a x v x_v xv , _, , w _w w重新定义为:
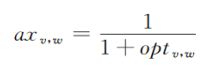
其中op t v t_v tv , _, , w _w w表示抗体v和抗原 ω \omega ω的结合强度,即抗体v在目标函数 ω \omega ω中的解和此函数最优解的接近程度,至于算法的其他步骤,变化不大。
2.求解更一般问题的免疫算法
7.3 常用免疫算法
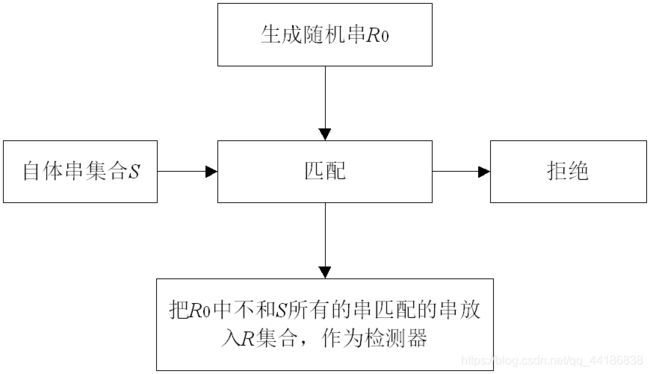
7.3.1 负选择算法
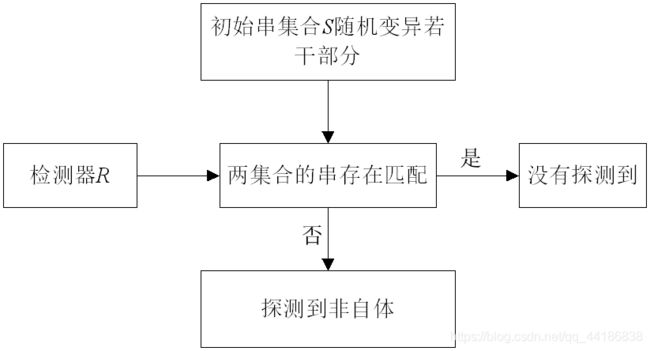
算法基本思想:需要两个字符串组成的集合R和R,通过先求一个和S不匹配的R集合,然后用R集合判断S集合是否发生了变化。
算法分成两部分,第一步是初始化R,第二步监视保护数据S。
初始化监测器R
7.3.2 克隆选择算法
克隆选择原理图
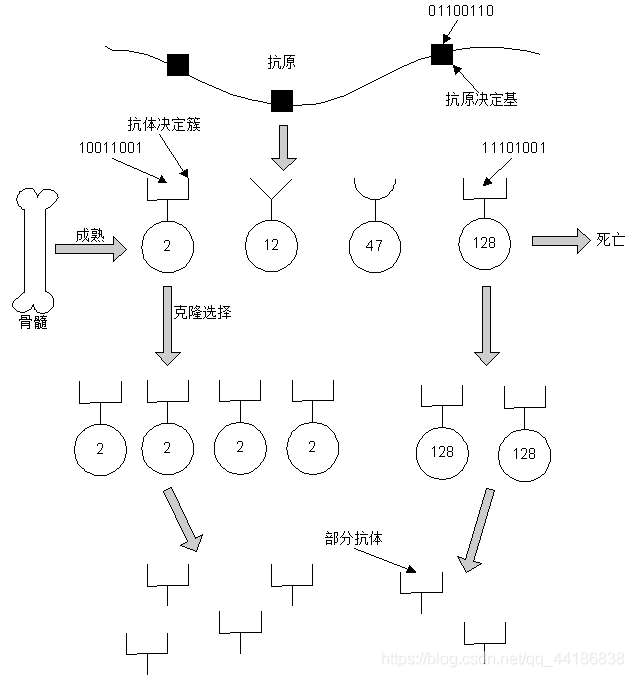
克隆选择流程图
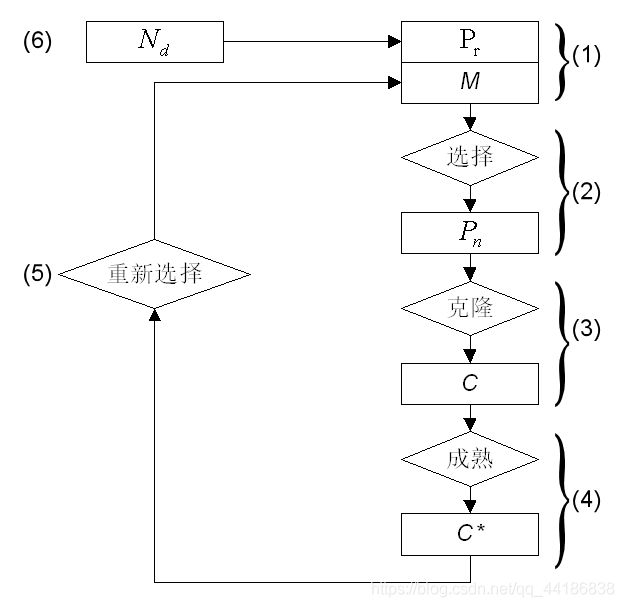


具体理解希望大家能结合代码实现具体应用问题来理解。
7.3.3 免疫算法与智能计算
免疫遗传算法
7.4 免疫算法的应用
识别与分类问题
优化问题
机器人学习与控制
数据挖掘等
第8章 分布估计算法
8.1 分布估计算法简介
8.1.1 产生背景
为啥分布估计算法会出现呢?或者说它出现是为了解决什么问题呢?
大家看到这的时候,或者或少也都了解过遗传算法了。这里简单回顾一下:遗传算法通过初始化种群,计算种群每个个体的适应度,然后通过交叉和变异得到新的种群,以此接近最优解。那在这个过程中,其实它面向的往往是具体到个体的层面(“积木块”),这样子导致当面对高维的问题时其性能较差。
所以这个时候如果我们想要解决这些问题,那就需要将面向层面提高到种群上,如果我们把种群的分布规律分析出来,是不是就可以用来提高算法的性能呢?
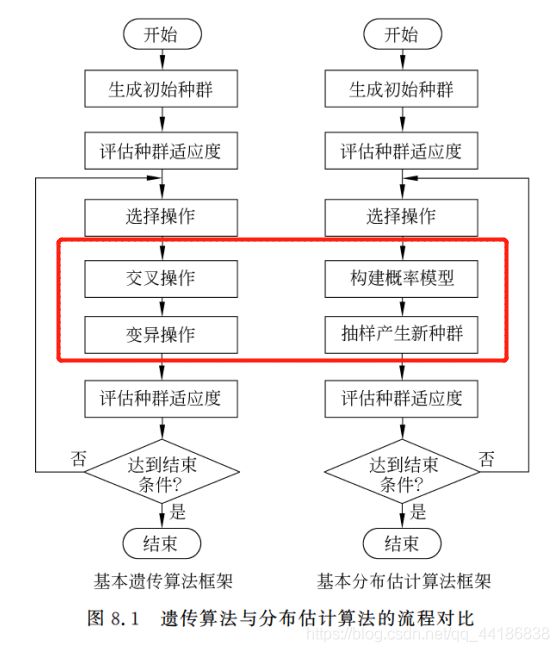
改进遗传算法的交叉操作和变异操作,防止破环积木块.采用概率模型和抽样的隐式形式产生新个体。
即以一种带有“全局操控”性的操作模式替换掉遗传算法中对“积木块”具有破坏作用的遗传算子(选择算子、交配算子和变异算子),这就是我们所要描述的分布估计算法。
8.1.2 分布估计算法的发展历史
开山始祖
PBIL:(1994 Baluja)
UMDA: (1996 H.Miihlenbein & Paass)
早期的算法专注于二进制编码
MIMIC: (1997 J.S.D.Bonet)
COMIT:(1997 S.Baluja)
FDA: (1999 HM Uhlenbein)
BOA: (1999 M.Pelikan)
逐渐扩展到连续分布估计算法
PBILc (Sebag, 1998)
UMDAc (Larrañaga, P., et al, 2000)
CEDGA (Q. Lu, 2005)
FWH & FHH (Tsutsui et al , 2001)
sur-shr-HEDA(N. Ding, et al, 2006)
混合分布估计算法
EDA与粒子群优化的混合
EDA与遗传算法的混合
EDA与差分进化算法的混合
并行分布估计算法
主从模式
岛屿模型
8.2 基本流程
8.2.1 基本的分布估计算法
分布估计算法的通用流程
Randomly generated the initial population P(0);
t = 0;
While not met the termination condition do
Begin
Select a set of promising individuals D(t) form the current population P(t);
Estimate the probability distribution of the selected set D(t);
Generate a set of new individuals N(t) according to the estimate;
Create a new population P(t+1) by replacing some individuals of P(t) by N(t);
t = t+1;
end
以UMDA为例,其算法执行步骤如下。
第一步:随机产生N个个体来组成一个初始群体,并评估初始种群中所有个体的适应度。
第二步:按适应度从高到低的顺序对种群进行排序,并从中选择出最优的Se个个体(Se ≤ \leq ≤N)。
第三步:分析所选出的Se个个体所包含的信息,估计其联合概率分布p(x)。
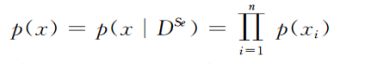
其中,n为解的维数,p( x i x_i xi)的边缘分布。
第四步,从构建的概率模型p(x)中采样,得到N个新样本,构成新种群。此时,若达到算法终止条件则结束,否则执行第二步。
**从第三步的公式可以看出在估计概率模型时认为变量之间是独立不相关的。**但实际上往往不是这样,后面会提到。
8.2.2 一个简单分布估计算的例子
现在,我们采用UMDA来求解一个四维的OneMax问题。在这个例子中,我们用一个简单的概率向量p=( p 1 p_1 p1, p 2 p_2 p2, p 3 p_3 p3, p 4 p_4 p4)来表示描述种群分布的概率模型,其中 p i p_i pi表示 x i x_i xi取1的概率,(1— p i p_i pi)则为 x i x_i xi取0的概率。
第一步:产生初始种群。为了使初始种群在定义域内符合均匀分布,我们定义初始化概率向量模型p=(0.5,0.5,0.5,0.5),然后根据p产生规模为10的初始种群,最后根据F(x)= x 1 x_1 x1+ x 2 x_2 x2+ x 3 x_3 x3+ x 4 x_4 x4,计算出初始种群的适应度,最终的结果如下表所示。
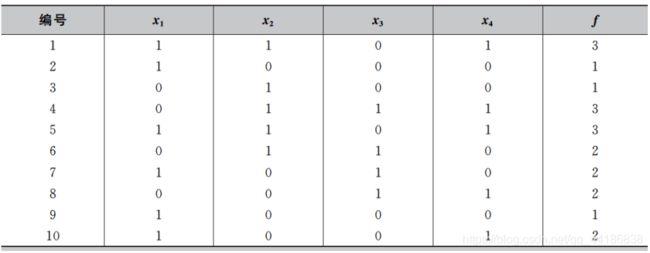
第二步:按照种群的适应度从高到低进行排序。假设Se=5,则从种群中选出适应度较高的5个个体用来更新概率向量模型p。更新概率模型时令 p i p_i pi = n i n_i ni/Se,这里 n i n_i ni 为在选出的较优个体中 x i x_i xi =1的个体数。最终选出的个体如下表所示,从而得到新的概率模型为p=( 3 5 \frac{3}{5} 53, 4 5 \frac{4}{5} 54, 3 5 \frac{3}{5} 53, 3 5 \frac{3}{5} 53) = (0.6,0.8,0.6,0.6)。
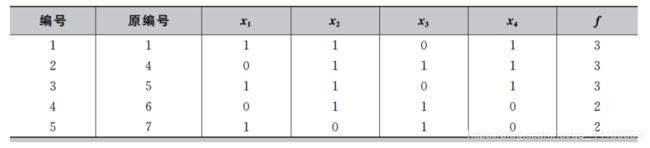
第三步:根据更新后的概率模型p产生新的样本,并计算这些新样本的适应度。最终得到新一代的种群如下表所示。
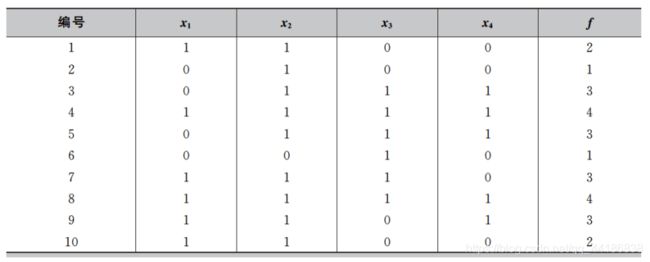
通过以上三步,分布估计算法完成了第一代的进化过程。接着重复第二步和第三步完成下一代的进化,最终得到的种群平均适应度和概率模型如下表所示。我们可以看出,随着演化的进行,种群的整体质量不断提高,概率向量逐渐逼近全局最优解。

8.3 分布估计算法的改进及理论研究
8.3.1 概率模型的改进
还记得我们前面提到的假设变量独立不相关吗?
早期很多分布估计算法都是这种,但现实生活中很多并非独立,而是相互关联,所以不难发现,这些算法最终应用都无法给人一个很满意的效果。
基于此,学者们提出了一系列用于求解具有变量相关性的问题的分布估计算法。
根据对于变量关联性捕捉能力的差异,可将其分为三大类。如下图所示。
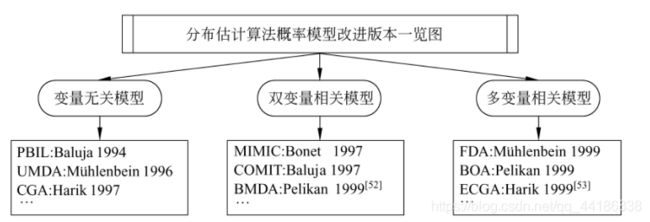
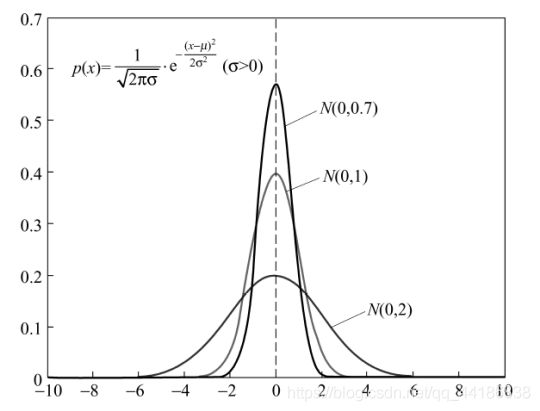
在这里我就以高斯概率模型中的PBILc为例,介绍高斯概率模型解决连续空间的优化问题的流程。
ok,下面正式介绍PBILc的流程。
基于高斯模型的EDA的流程如下:

不难发现,第二步和第三步是最重要的步骤,更新概率模型中的两个重要参数:均值和方差。其实更新的方式多种多样,也可以直接用优秀个体的均值和方差替代原来的均值与方差。
8.3.2 混合分布估计算法
以DE-EDA为例。
第一步: 从种群中选出M个较优的个体,建立如下概率模型 :
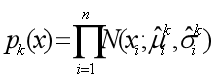
第二步: 产生一个0~1之间的随机值v,若v≤α,则按照DE方式产生新个体,否则按照EDA的方式取样产生新个体。
第三步: 若新个体的适应度大于原个体的的适应度则替换之。
第四步:若产生了足够数量的新种群则终止,否则执行第一步 。
8.3.3 并行分布估计算法
种群级别并行化
思路: 将种群分成多个子种群,每个子种群在不同的机器上运行,然后各个子种群通过迁移等机制进行通信,达到综合信息的目的
![]()
适应度评估并行化
思路:适应度评估通常是算法中最耗时的部分,因而,采用多台机器并行计算种群中的适应度可有效提高算法求解速度
![]()
概率模型构建并行化
思路:设计复杂的概率模型需要较大的计算量,并行求解复杂概率模型可有效提高算法计算速度.
其他并行机制
采样的操作进行并行化
混合并行机制
8.4 分布估计算法的应用
分布估计算法的应用领域(函数优化)
有效地保护 “积木块”,能够高效求解高维的复杂函数优化问题.
在具有先验知识的情况下,可有针对地选择概率模型,从而设计出性能优越的分布估计算法.
已成功应用于求解复杂的多峰函数, 关联性强的复杂函数优化以及多目标函数优化.
分布估计算法的应用领域(组合优化)
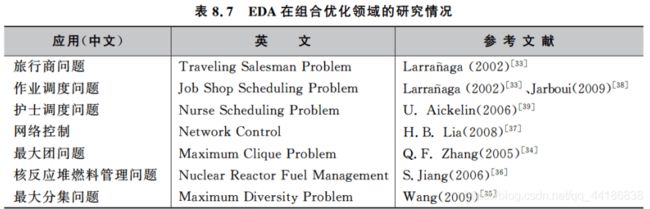
分布估计算法的应用领域(生物信息学及其它)
分布估计算法 在处理高维复杂问题时表现出良好的性能,非常适合于求解含有海量信息的生物信息学领域的问题。
基因结构分析。
DNA微阵列数据的分类和聚类分析。
蛋白质结构预测与蛋白质设计。
分布估计算法在多目标优化、机器学习、模式识别和聚类分析等领域也取得了成功的应用。
第9章 Memetic算法
9.1 Memetic算法的基本思想
在讲Memetic算法之前,我们先来了解一下meme。

基于图中内容,Mosato(1989)提出了Memetic算法。
那么,Memetic算法出现的原因是啥呢?Memetic算法是啥呢?
那在讲Memetic算法之前,我们先来稍微回忆一下遗传算法、蚁群优化算法、粒子群优化算法等这些进化算法以及群体智能优化算法,这些算法有啥共性呢?
好吧,共性其实很多。这里我想讲的是:在面对大规模、复杂的优化问题时,这些算法往往存在着收敛速度慢、难以寻找高精度的解的缺点。
而在这些算法的基础上,引入局部搜索方法,对计算智能方法所发现的解进行改进,将有效地提高计算智能方法的求解效率和精度。
以上就是其出现的大致原因。基于此,我们不难发现,Memetic算法其实就是基于群体的计算智能方法与局部搜索方法相结合的一类新型的优化技术。
9.2 Memetic算法的框架
为系统分析MA,Krasnogor和Smith提出了MA的框架模型,根据该框架,一个MA应该包含如下9种要素:
![]()
其中:
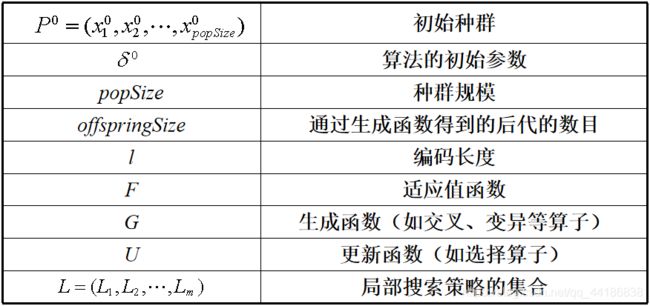
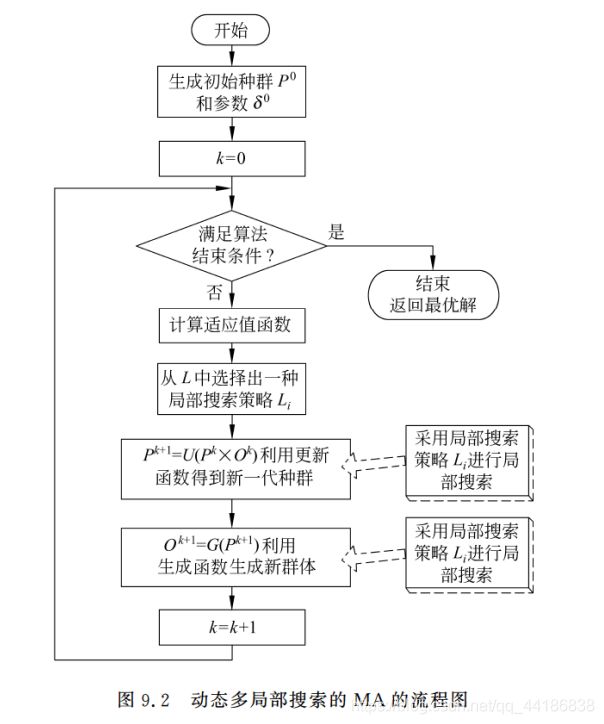
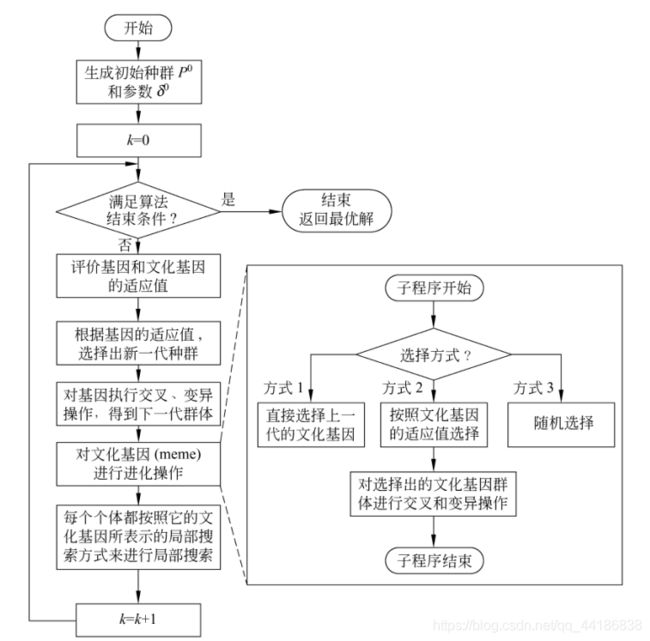
下图为MA的基本流程框架
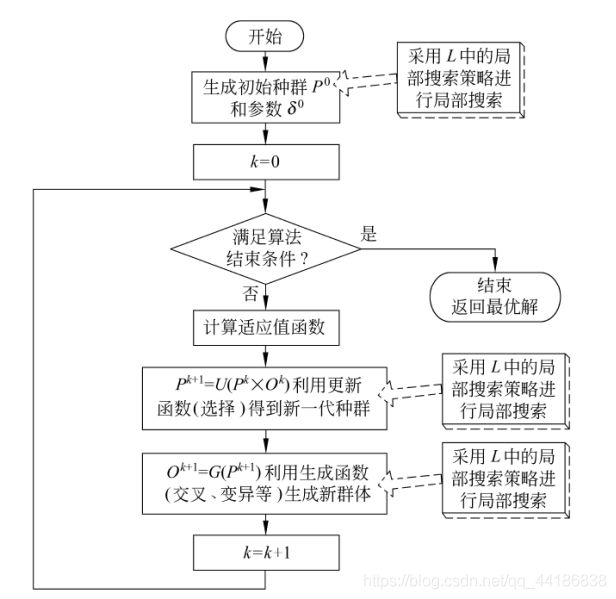
不难发现,与传统的进化方法相比,MA实际上知识增加了一个局部搜索操作,即增加了L = ( L 1 L_1 L1, L 2 L_2 L2, …, L m L_m Lm) 这个要素(大部分MA的m值为1,即只适用一种局部瘦身策略)。
通过上图我们也可以发现,局部搜索可以与全局搜索策略的生成函数(例如GA中的交叉、变异操作)相结合,也可以与更新函数(例如GA中的选择操作)相结合。注意:有些文献中也把局部搜索作用域初始解,以提高初始解的质量,但这一般只作为一种辅助方法。
另外,补充一下,局部搜索的执行可以依据Lamarckian模型,也可以依据Baldwinian模型;可以作用于群体中的某个个体之中,也可以作用于整个群体。
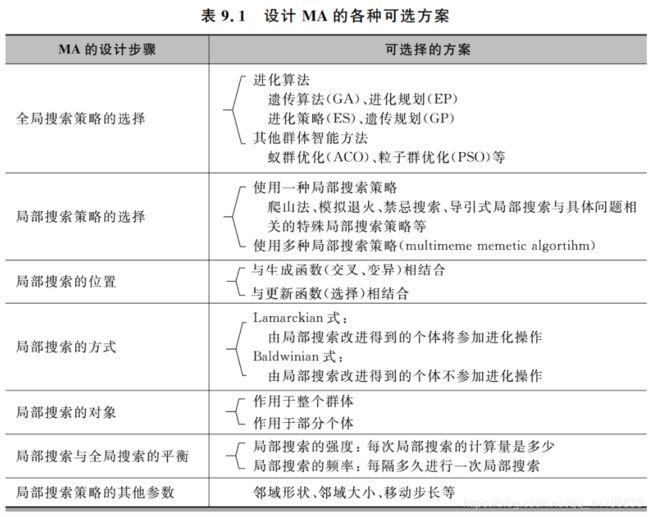
对于一个MA来说,局部搜索的选择以及全局搜索与局部搜索的结合方式将直接影响到算法性能的好坏。因此,设计一个高性能的MA必须考虑以下四方面的问题:
(1)应该选择什么局部搜索策略;
(2)应该在什么时候执行局部搜索;
(3)应该针对哪些个体进行局部搜索,应该采用Lamarckian模型还是Baldwinian模型;
(4)如何平衡算法的全局搜索能力和局部搜索能力。
基于此,下面将会给大家介绍多种针对MA的分类方式以及对应的几种Memetic算法。
9.3 静态Memetic算法
静态Memetic算法的特点
一般只采用一种局部搜索策略。
局部搜索的执行位置和方式都预先确定,在算法执行过程中保持不变。
9.3.1 局部搜索的位置
可以根据局部搜索的位置不同,分为:
与生成函数相结合的局部搜索,以及与更新函数相结合的局部搜索。
9.3.2 Lamarckian模式Baldwinian模式
简单介绍一下这两种模式。
在进化算法中引人局部搜索的主要模式包括Lamarckian模式(可译作拉马克式)和Baldwinian模式。Lamarckian模式指的是“后天获取的特性也可以遗传”,也就是说,在采用局部搜索策略改进了某个个体之后,改进了的个体将(代替原有个体)参与全局搜索方法的进化操作。相反地,在 Baldwinian模式中,被局部搜索策略改进了的个体不会代替原有个体参与进化操作,交叉、变异等进化算子仍然只作用于未被局部搜索改进的个体上。
9.4 动态Memetic算法
9.4.1 动态Memetic算法
动态MA是一种动态调整局部搜索策略。
分类
按照动态调整类型,分成三类:
静态型—按照静态的规则来调整
适应型—利用在线反馈的信息来调整
自适应型—将局部搜索设置信息也编码到算法当中一起进化(协同进化的MA)
按照自适应的层次,分成三类:
外部型—利用外部的先验知识(一般属于静态型)
局部型—采用了局部反馈信息来调整
自适应型—采用了全部反馈信息来调整
9.4.2 Meta-Lamarckian学习型MA
Meta-Lamarckian学习型MA:每次执行局部搜索之前,从局部搜索策略池中选择一种局部搜索方案。
基本Meta-Lamarckian学习方案
基本Meta-Lamarckian学习方案采用了一种简单的随机游走方案来选择局部搜索策略。在这种方案下,算法每次执行局部搜索之前都从局部搜索策略池中随机地选择一种局部搜索方法。显然,这种方案并没有借鉴任何在搜索过程中在线得到的反馈信息,因此属于静态,外部型的MA。
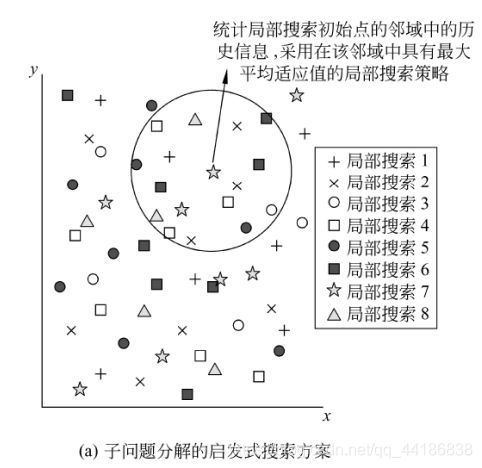
子问题分解的启发式搜索方案
子问题分解的启发式搜索方案的Meta-Lamarckian学习方式如下图所示。
在MA的最初前g次迭代中(g是一个预先设定的参数),算法仍然采用随机游走的方式来选择局部搜索策略。随后,算法在每次执行局部搜索之前,首先从局部搜索初始点的邻域中寻找k个曾经搜索过的点(例如,可以选择离局部搜索初始点的欧几里德距离最近的k个曾经搜索过的点),统计在这k个点上曾经使用过的局部搜索策略所对应的适应值。最后,算法将采用在该邻域内具有最大平均适应值的局部搜索策略。
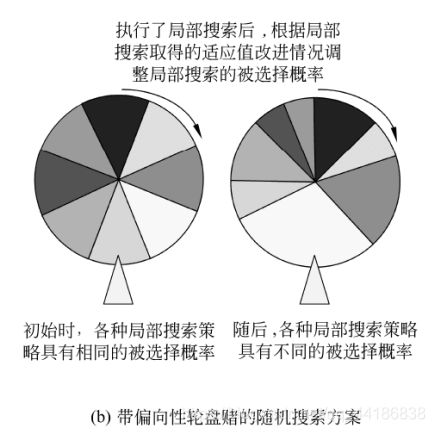
带偏向性轮盘赌的随机搜索方案
带偏向性轮盘赌的随机搜索方案的Meta-Lamarckian学习方式如下图所示。
这种MA采用了轮盘赌机制来选择局部搜索策略。在算法开始时,各种局部搜索策略被选择的概率是相同的。算法首先按照随机给定的次序把每一种局部搜索策略都执行一次,并根据各种局部搜索策略所带来的适应值改进幅度来调节局部搜索被选择的概率。随后,算法在每次执行局部搜索之前都采用轮盘赌方式选择一种局部搜索策略,并在局部搜索执行完毕后更新该局部搜索策略被选择的概率。
9.4.3 超启发式Memetic算法
随机超启发式
随机地选择局部搜索策略。
贪心超启发式
选择能够得到最大改进幅度的局部搜索策略
基于选择函数的超启发式
根据局部搜索策略的选择函数F值来选择局部搜索策略。
9.4.4 协同进化Memetic算法
局部搜索的具体设置(包括局部搜索策略、局部搜索的执行方式以及局部搜索深度、频率、邻域大小等各种参数编码成文化基因)也编码到个体的基因中,共同进化。
下图为协同进化MA的流程图。
目前MA已应用于众多复杂优化问题。
第10章 模拟退火与禁忌搜索
10.1 模拟退火算法
10.1.1 算法思想
一听这个名字我想多数人头脑都会冒出“???”,这咋还得退火嘞,难不成还能上火的吗?
其实模拟退火(SImulated Annealing)算法的思想就是来源于物理的退火原理,也就是降温原理。先在一个高温状态下(相当于算法随机搜索),然后逐渐退火,在每个温度下(相当于算法的每一次状态转移)徐徐冷却(相当于算法局部搜索),最终达到物理基态(相当于算法找到最优解)。
10.1.2 基本流程
先附上模拟退火算法求解最优化问题的基本流程图和伪代码
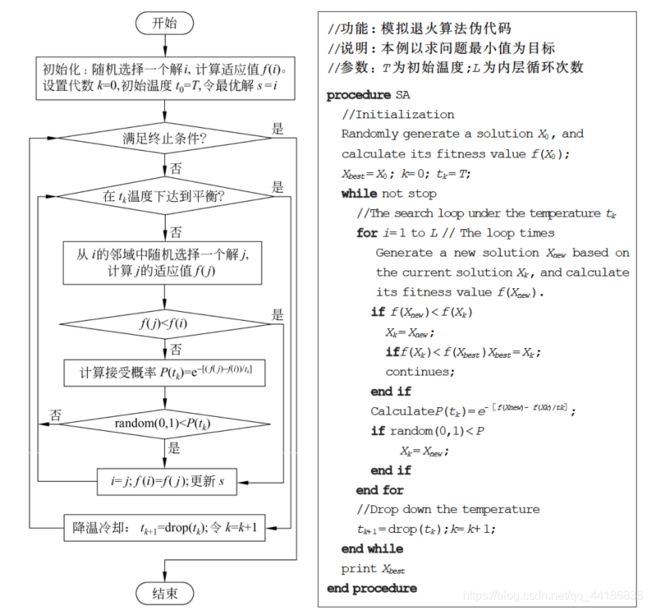
先声明:上图给出的只是模拟退火算法的基本框架,针对具体问题时还需要具体的设计。
从图中我们不难发现发现,模拟退火其实有两层循环,分为内循环和外循环。
内循环模拟的是在给定温度下系统达到平衡的过程。在内循环中,每次都从当前解i的邻域(怎么构建邻域后面会讲)中随机找出一个新解j,然后按照Metropolis准则(后面会给公式)概率地接受新解。那啥时候达到热平衡呢?你可以定义为循环一定的代数,或者基于接受率定义平衡等。
外层循环是一个降温的过程,当内循环结束,即在一个温度下达到平衡后,开始外层的降温,然后再新的温度下重新开始内循环。
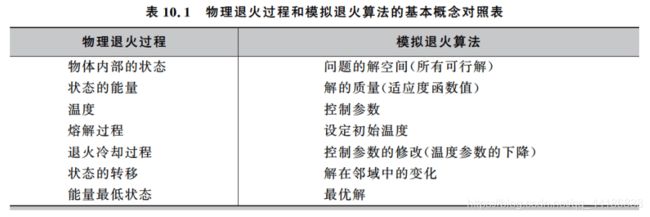
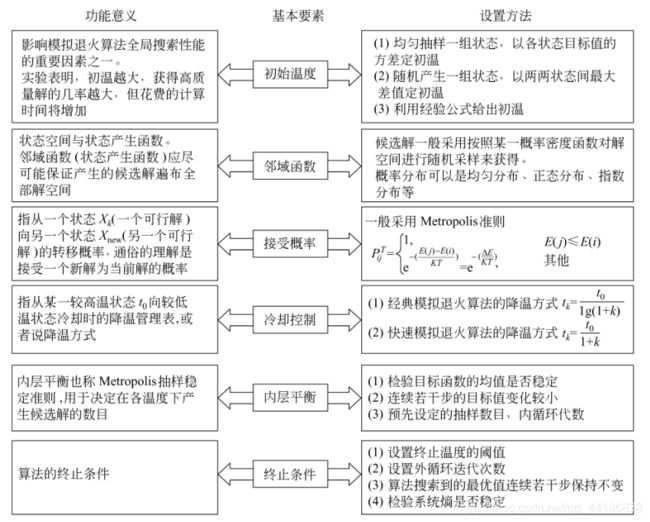
模拟退火算法在求解最优化问题的时候,会包含以下几个方面的基本要素。分别为:初始温度、邻域函数、接受概率、冷却控制、内层平衡、终止条件。具体意义以及设置方法如下图所示。
10.1.3 应用举例
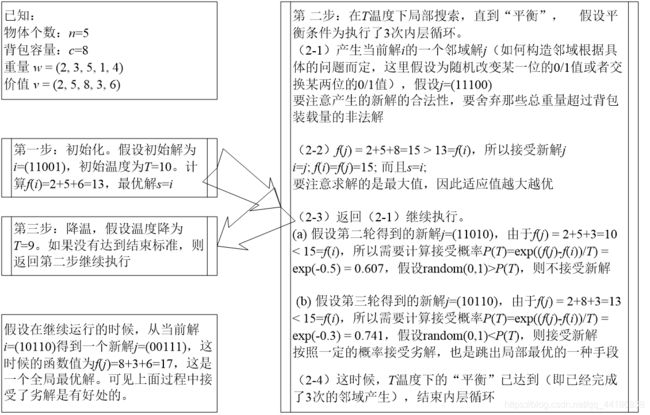
问题:已知背包的装载量为c=8,现有n=5个物品,它们的重量和价值分别是(2, 3, 5, 1, 4)和(2, 5, 8, 3, 6)。试使用模拟退火算法求解该背包问题,写出关键的步骤。
在开始求解之前我们先分析一下问题。
分析:背包问题本身是一个组合优化问题,也是一个典型的NP难问题。如果使用枚举的方法,我们需要找到n个物品的所有子集,然后在那些满足约束条件的子集中比较物品的总价值,找到总价值最大的子集,也就是问题的最优解。但是我们知道,大小为n的集合的子集数目为 2 n 2^n 2n ,所以当背包问题的规模变大(n变大)的时候,要找出所有的子集是一个不现实的做法,因为计算复杂度的指数级增长已经使得问题在规模稍大的时候就无法在可以接受的时间内得到解决。因此背包问题需要采用一些计算复杂度较低的,但是能够提供令人满意的解的算法,而模拟退火算法是解决背包问题的重要手段。
大量的实验证明,模拟退火算法能够处理规模较大的背包问题,而且能够鲁棒地得到满意的解。
求解:假设问题的一个可行解用0和1的序列表示,例如i=(1010)表示选择第1和第3个物品,而不选择第2和第4个物品。用模拟退火算法求解例10.1的关键过程如图所示:
10.2 禁忌搜索算法
10.2.1 算法思想
禁忌搜索(Tabu Search, TS)也是属于模拟人类智能的一种优化算法。
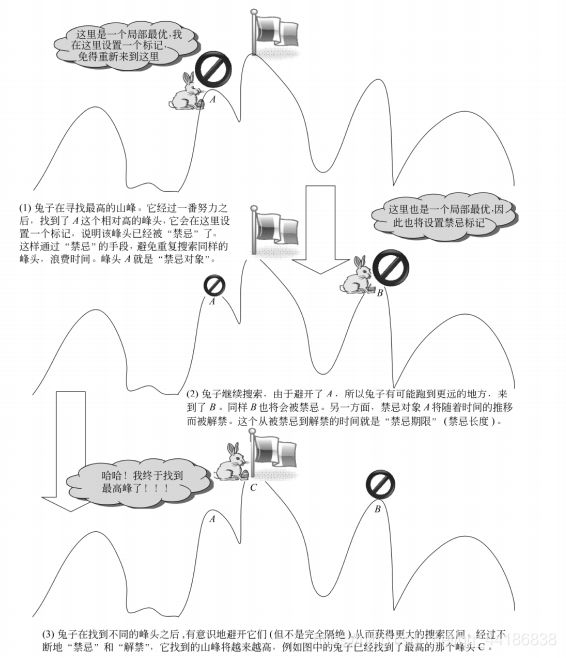
上图涉及到了禁忌搜索中的一些基本概念,现在来对这些概念作解释。
禁忌表(Tabu List,TL)
是用来存放(记忆)禁忌对象的表。它是禁忌搜索得以进行的基本前提。禁忌表本身是有容量限制的,它的大小对存放禁忌对象的个数有影响,会影响算法的性能。
禁忌对象(Tabu Object,TO)
是指禁忌表中被禁的那些变化元素。禁忌对象的选择可以根据具体问题而制定。例如在旅行商问题(Traveling Salesman Problem,TSP)中可以将交换的城市对作为禁忌对象,也可以将总路径长度作为禁忌对象。
禁忌期限(Tabu Tenure,TT)
也叫禁忌长度,指的是禁忌对象不能被选取的周期。禁忌期限过短容易出现循环,跳不出局部最优,长度过长会造成计算时间过长。
渴望准则(Aspiration Criteria,AC)
也称为特赦规则。当所有的对象都被禁忌之后,可以让其中性能最好的被禁忌对象解禁,或者当某个对象解禁会带来目标值的很大改进时,也可以使用特赦规则。
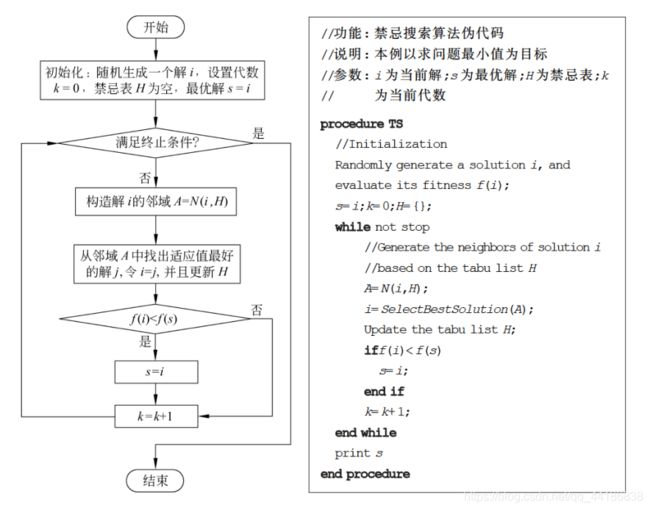
10.2.2 基本流程
禁忌搜索算法在初始化的时候,在搜索空间随机生成一个初始解 i,禁忌表H置空,当前解i记为历史最优解 s,然后进入迭代的搜索过程。在每一次迭代中,都从当前的解i出发,在当前禁忌表H的限制下,构造出解i的邻域A,然后从A中选出适应值最好的解 j 来替换解 i,同时更新禁忌表H。在解 j 替换解 i 之后,如果解 i 的质量得到改善,那么历史最优的解 s 将被解 i 替换;否则,s 保持不变,即使解 i 虽然暂时变差了,但是由于扩大了搜索空间,仍有利于跳出局部最优。得到了新的当前解 i 之后,算法返回迭代的开始继续进行,直到找到最优解或者运行了一定的迭代次数等终止条件的时候结束算法。
基本流程图和伪代码如下:
10.2.3 应用举例
啥?上面听不懂?那麻烦给我点个赞,然后看一看下面的内容哈哈。
问题:已知一个旅行商问题为四城市(a,b,c,d)问题,城市间的距离如矩阵D所示,为方便起见,假设邻域映射定义为两个城市位置对换,而始点和终点城市都是a。请分析使用禁忌搜索算法求解该问题的前面三代的过程与主要步骤。
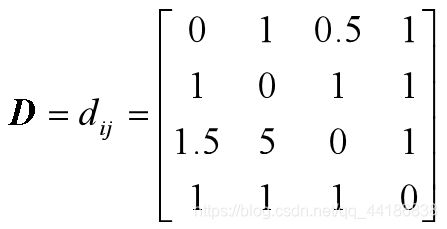
在开始求解之前我们先分析一下问题。
分析:这是一个简单的问题,利用枚举的方法也可以找到最优的答案,但是,找到答案不是我们的目的,我们主要是想通过一一个简单的例子来理解禁忌搜索是如何进行工作的。从距离矩阵D可以看到,这是一个非对称的TSP问题,但是这并不影响算法的执行。由于题目假设了邻域构造的方式,而且规定了始点和终点都是城市a,因此,在以下的求解过程中,我们不使用城市a和其他城市进行交换,这样的操作并不会影响全局寻优的能力。
求解:

注:在实际应用中,通过选择更高的禁忌对象,设置合理的禁忌期限,或者采用其他更好的的参数,都可以避免循环(反复出现同种情况的邻域值)的出现,提高算法的性能。
结束语
完结啦!
整理不易,十分的费时费力!
好希望大家能有收获!