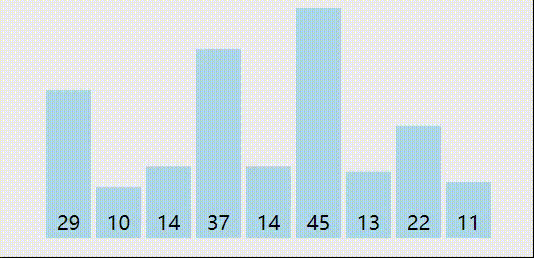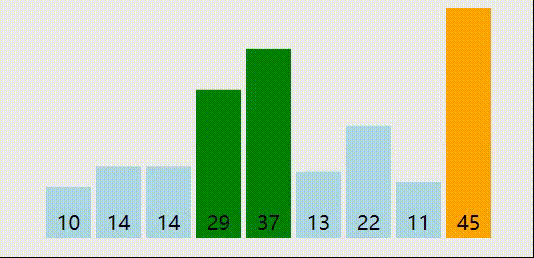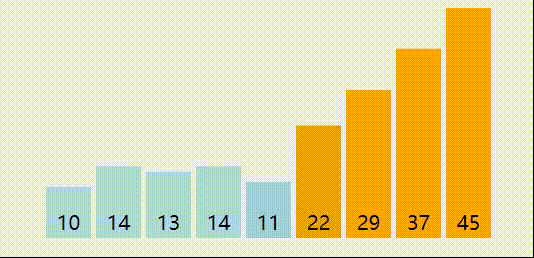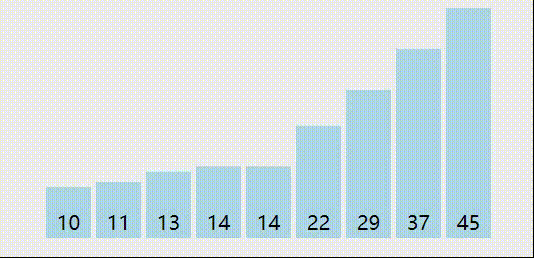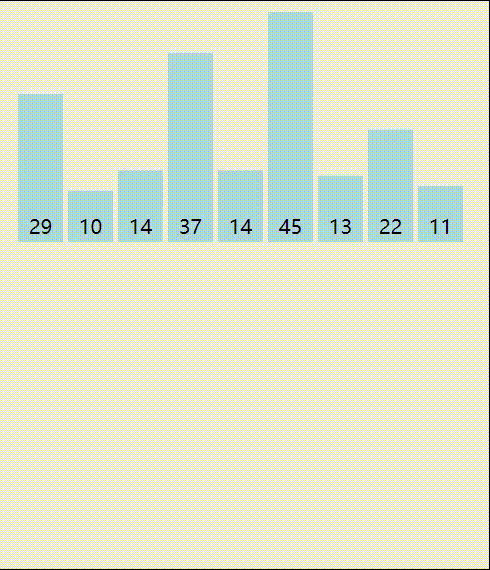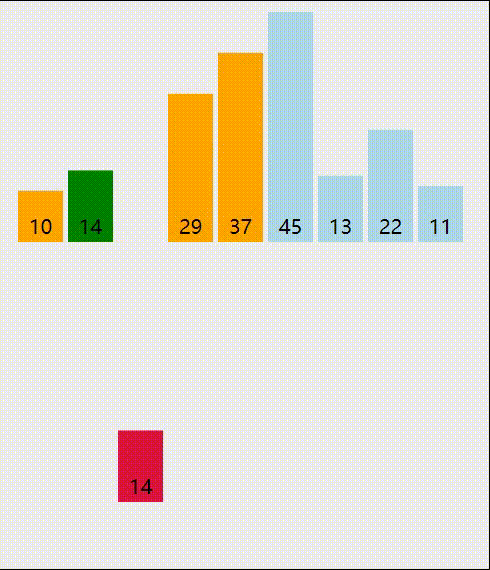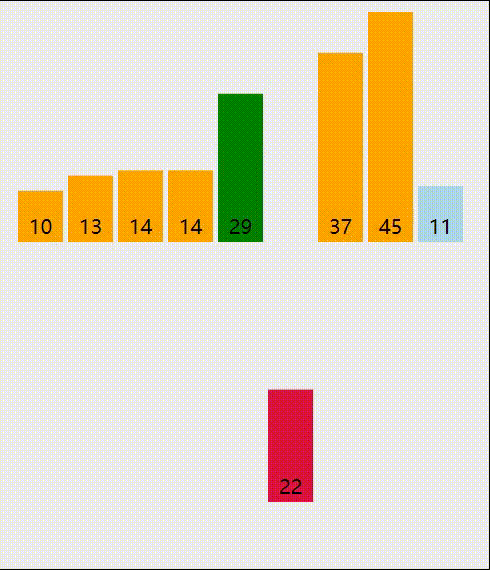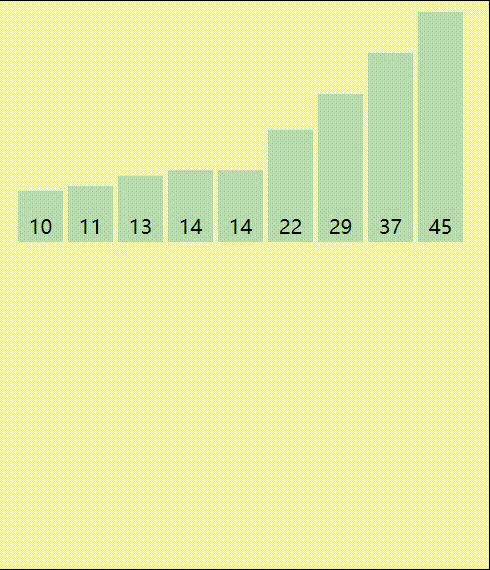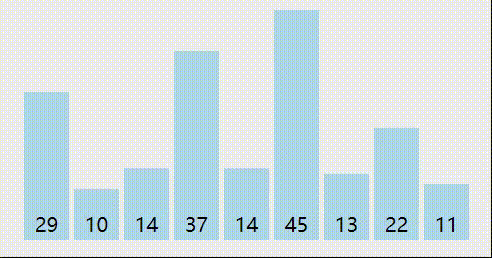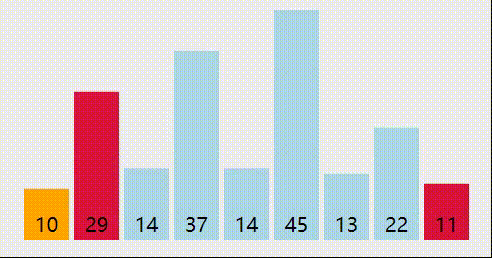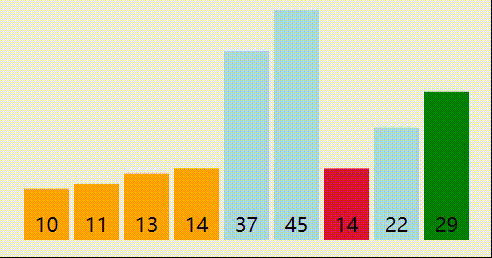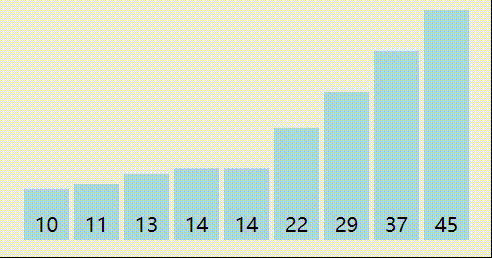文章结构
- 概述
- 冒泡排序
- 插入排序
- 选择排序
1. 概述
常见的排序算法有:冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序
衡量排序算法的标准
- 时间复杂度
- 空间复杂度
- 是否稳定
按照时间复杂度,可以将上面的算法划分为
| 时间复杂度 | 算法名称 |
|---|---|
| O(n^2) | 冒泡、插入、选择 |
| O(nlogn) | 归并、快排 |
| O(n) | 计数、基数、桶 |
这篇文章我们先来看一下几个时间复杂度为O(n^2)的排序算法:冒泡排序、插入排序、选择排序
2. 冒泡排序
2.1 什么是冒泡排序
冒泡排序的思想就是:比较相邻两个元素的大小,如果满足大小关系,则用第二个元素和下一个元素继续比较;如果不满足大小关系,则交换两个元素的位置,然后用交换后的第二个元素和下一个元素继续比较,依次比较到最后一个元素。通过这样一轮冒泡排序之后,最大的元素就到了最后的那个位置上。再次重复这个过程将次大的元素排好,重复n次则所有的元素都排好了
优化技巧:如果某一轮冒泡排序中,没有元素需要交换,则整个待排序的数据已经有序了,则不需要再进行排序了。
2.2 动画演示
2.3 过程分析
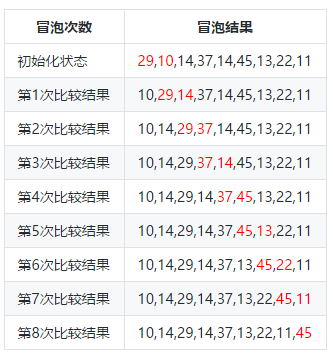
我们来分析一轮冒泡排序的过程,使用红色标记相邻两个待比较的元素
第一轮比较结束,我们将待排序列表中的最大元素45排到了最后面。然后我们继续按照这个思路,对前面的n-1个元素继续排序。
2.3 代码实现
public static void sort(int[] array) {
if (array == null || array.length == 1) {
return;
}
int size = array.length;
for (int i = 0; i < size; i++) {
boolean isExchanged = false;
for (int j = 0; j < size - i - 1; j++) {//这里的i表示经过了几次冒泡排序了,经过一次有在最后面多了一位已经排好序的元素,所以下一次要比较的范围也较少1
if (array[j] > array[j + 1]) {//只有在后面的元素大于前面的元素的时候才交互,可以保证排序的稳定性
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
isExchanged = true;
}
}
if (!isExchanged) {//当某一趟冒泡排序中没有交换发送的时候,说明序列已经有序了
break;
}
}
}
2.4 性能分析
时间复杂度分析
- 最好时间复杂是O(n):当待排序的列表本身的顺序和要求的顺序一致的时候,我们只需要进行一轮冒泡排序,发现没有数据需要交换,我们就知道列表已经满足要求的顺序了,不需要再继续排序,此时时间复杂度为O(n)
- 最差时间复杂度O(n^2):当待排序的列表本身的顺序和要求的顺序完全相反的时候,我们需要进行n-1轮冒泡排序
- 平均时间复杂度O(n^2)
空间复杂度
冒泡排序整个排序过程中,只需要借助一个额外的辅助空间,所以空间复杂度为O(1),我们把这种空间复杂度为O(1)的排序叫做原地排序
是否稳定
什么是稳定排序:稳定排序排序就是排序前值相同的元素之间的相对位置和排序之后的相对位置一样。比如有两个元素的值都是14,如果排序之后,原来在前面的14,现在排到了后面去了,那就不是稳定排序;如果依然排在前面,则是稳定排序
冒泡排序是稳定排序:冒泡排序过程中只是对相邻元素进行交换,我们可以控制当相邻两个元素的值一致时,不进行交互,这样就可以保证稳定性
3. 插入排序
3.1 什么是插入排序
插入排序的思想是将序列分为两个:一个有序序列,一个无需序列;然后遍历无序序列,依次取出元素插入到有序序列中的合适位置,使得有序序列依然有序,无序序列遍历完了,整个序列就都有序了
3.2 动画演示
3.3 过程分析
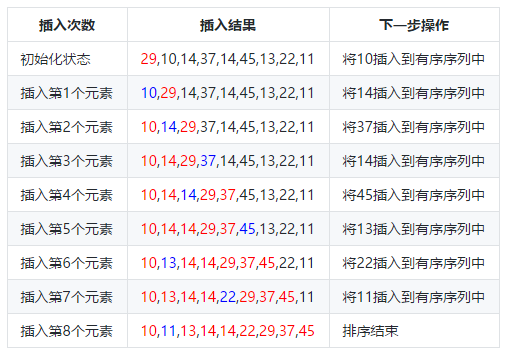
我们来分析一下插入排序的过程,有序序列我们用红色标记,刚刚插入的值我们使用蓝色标记
3.4 代码实现
public static void sort(int[] a) {
if (a == null || a.length == 0) {
return;
}
int size = a.length;
for (int i = 1; i < size; i++) {
int temp = a[i];
int index = i - 1;
while (index >= 0 && temp < a[index]) {//从后向前比较,寻找插入元素的位置,只有小于的时候,才移动原来的序列,保证排序的稳定性
a[index + 1] = a[index];
index--;
}
a[index + 1] = temp;
}
}
3.5 性能分析
时间复杂度
- 最好时间复杂是O(n):当待排序的列表本身的顺序和要求的顺序一致的时候,我们只需进行一轮遍历,不需要查找插入位置和执行插入操作
- 最差时间复杂度O(n^2):当待排序的列表本身的顺序和要求的顺序完全相反的时候,每一个元素都需要和有序序列中所有的元素进行比较已查找插入的位置,并执行插入操作
- 平均时间复杂度O(n^2)
空间复杂度
也只需要借助一个辅助空间,所以空间复杂度为O(1)
是否稳定
插入排序过程中,在查找插入位置的时候,控制好不要将后面与前面值相等的元素插入到相同值的前面就可以保证稳定性。所以插入排序是稳定的。
4. 选择排序
4.1 什么是选择排序
选择排序也是将序列分为两个序列:一个有序(初始化为空),一个无序(待排序的序列)。然后从无序序列中选择最小的元素放到有序序列的最后(和无序序列中的第一个元素交换位置),直到无序序列中没有元素
4.2 动画演示
4.3 过程分析
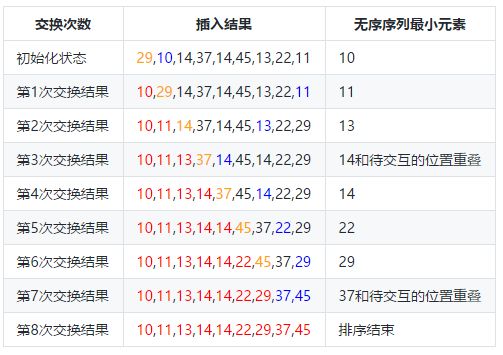
我们依然29,10,14,37,14,45,13,22,11这样一个待排序序列来分析一下排序过程。有序序列我们用红色标记,无序序列的最小值,我们用蓝色标记,无序序列中要交换的位置我们用橙色标记
4.4 代码实现
public static void sort(int[] array) {
if (array == null || array.length == 0) {
return;
}
int size = array.length;
for (int i = 0; i < size - 1; i++) {
//从无序序列中找到最小的元素
int index = i;
for (int j = i + 1; j < size; j++) {
if (array[index] > array[j]) {
index = j;
}
}
//无序序列中的最小值和无序序列中的第一个元素交换位置(因为这里的交互元素的位置,所以选择排序不是稳定排序)
int temp = array[i];
array[i] = array[index];
array[index] = temp;
}
}
4.5 性能分析
时间复杂度
无论是否有序,从无序序列中选择最小元素都需要经过n次比较,所以选择排序的最好、最差、平均时间复杂度都是O(n^2)
空间复杂度
选择排序也只需要借助一个额外的辅助空间,所以选择排序的时间复杂度也是O(1)
是否稳定
选择排序不是稳定排序,因为选择排序的过程中存在将无序序列最小的元素和无序序列第一个元素交换的操作,可能把相同值的前一个元素交换到后面去了。
源码
源码和测试用例请查看github之排序