文章结构
- 如何理解回溯算法
- 回溯算法的经典应用
- 完整源码
- 图片来源
1. 如何理解回溯算法
1.1 什么是回溯算法
回溯算法也叫试探法,它是一种类似枚举的搜索尝试算法,通过在搜索的过程中寻求问题的解,当搜索到某一个步,发现已经不满足求解的条件时,就返回到上一步,然后尝试别的路径再继续搜索。
1.2 回溯算法解决问题的一般步骤
- 确定问题的求解包含多少个步骤
- 确定每个步骤包含多少中选择
- 以深度优先的方式寻找问题的解,并且在搜索过程中使用剪枝函数避免无效搜索
1.3 什么样的问题适合用回溯算法来求解
当一个问题涉及到多个步骤的选择,且每个步骤都有多个可选的选项,我们试图从中找出一个可能的解或者寻找最优解时,就可以使用回溯算法来求解
2. 回溯算法的经典应用
- 8皇后问题
- 0-1背包问题
2.1 8皇后问题
什么是8皇后问题:8皇后问题就是假设我们有一个 8x8 的棋盘,希望往里放 8 个棋子(皇后),每个棋子所在的行、列、对角线都不能有另一个棋子。让你求出一个可能的摆放方式
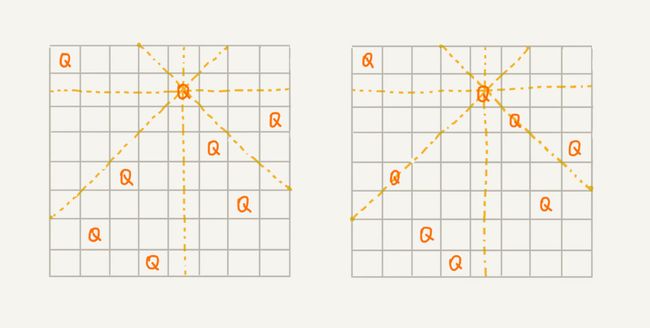
下图中:第一种摆放方式是8皇后问题的一个解,每个皇后所在的行、列、对角线都没有其他的皇后;第二种就不是。
问题分析:
- 8个皇后的摆放,就相当于8个选择的步骤
- 每个皇后可以摆放的位置,每一行或者每一列,也就是每个步骤可选择的范围
- 以深度优先搜索的方式,从第一个皇后的摆放开始,往后尝试每个皇后的摆放,当某个皇后在所在的行或者列上的任意位置都无法满足条件时,则说明这条路径无解了,回溯到上一步,再继续尝试。
寻找一种摆放方式
代码实现
public class CalQueen {
public static int[] calculate(int size) {
int locations[] = new int[size];//记录每一列上皇后的位置
for (int i = 0; i < size; i++) {
locations[i] = -1;
}
queens(locations, 0, size);
return locations;
}
/**
* 我们按列来摆放皇后,queens()方法判断某一列上的皇后可以摆放在哪个行上
*
* @param locations
* @param current
* @param size
*/
private static boolean queens(int[] locations, int current, int size) {
if (current == size) {
return true;
}
for (int i = 0; i < size; i++) {//i表示每一列上,皇后可选的位置
if (isOk(locations, current, i)) {//判断当前这个皇后是否可以摆放在这个位置
locations[current] = i;
if (queens(locations, current + 1, size)) {
return true;
}
}
}
return false;
}
private static boolean isOk(int[] locations, int current, int location) {
if (current == 0) {
return true;
}
//不再同一列(按列遍历,自然不会在同一列上)
//不在同一行(temp == locations[i] )
//不在一条斜边上(current - i == Math.abs(temp - locations[i]))
for (int i = 0; i < current; i++) {
if (location == locations[i] || current - i == Math.abs(location - locations[i])) {
return false;
}
}
return true;
}
}
测试用例
@Test
public void test1() {
int locations[] = CalQueen.calculate(8);
int size = locations.length;
for (int i = 0; i < size; i++) {
StringBuilder builder = new StringBuilder();
for (int j = 0; j < size; j++) {
if (locations[i] == j) {
builder.append(" Q ");
} else {
builder.append(" * ");
}
}
System.out.println("第" + i + "列:" + builder.toString());
}
}
测试结果
第0列: Q * * * * * * *
第1列: * * * * Q * * *
第2列: * * * * * * * Q
第3列: * * * * * Q * *
第4列: * * Q * * * * *
第5列: * * * * * * Q *
第6列: * Q * * * * * *
第7列: * * * Q * * * *
计算共有多少中摆放方式
代码实现
public class CalQueen {
private static boolean isOk(int[] locations, int current, int location) {
if (current == 0) {
return true;
}
//不再同一列(按列遍历,自然不会在同一列上)
//不在同一行(temp == locations[i] )
//不在一条斜边上(current - i == Math.abs(temp - locations[i]))
for (int i = 0; i < current; i++) {
if (location == locations[i] || current - i == Math.abs(location - locations[i])) {
return false;
}
}
return true;
}
private static int mSum = 0;
/**
* 计算总共有多少种解
* @param size
* @return
*/
public static int countSum(int size) {
int locations[] = new int[size];//记录每一列上皇后的位置
for (int i = 0; i < size; i++) {
locations[i] = -1;
}
mSum = 0;
queens2(locations, 0, size);
return mSum;
}
private static void queens2(int[] locations, int current, int size) {
if (current == size) {
mSum++;
}
for (int i = 0; i < size; i++) {//i表示每一列上,皇后可选的位置
if (isOk(locations, current, i)) {//判断当前这个皇后是否可以摆放在这个位置
locations[current] = i;
queens2(locations, current + 1, size);
}
}
}
}
测试用例
@Test
public void test2() {
for (int i = 1; i <= 8; i++) {
int size = i;
int sum = CalQueen.countSum(size);
System.out.println(size + "皇后问题,总共有" + sum + "种解");
}
}
测试结果
1皇后问题,总共有1种解
2皇后问题,总共有0种解
3皇后问题,总共有0种解
4皇后问题,总共有2种解
5皇后问题,总共有10种解
6皇后问题,总共有4种解
7皇后问题,总共有40种解
8皇后问题,总共有92种解
2.2 0-1背包问题
什么是0-1背包问题:0-1 背包问题有很多变体,我这里介绍一种比较基础的。我们有一个背包,背包总的承载重量是 Wkg。现在我们有 n 个物品,每个物品的重量不等,并且不可分割。我们现在期望选择几件物品,装载到背包中。在不超过背包所能装载重量的前提下,如何让背包中物品的总重量最大?
问题分析:
- n个物品就是n个步骤的选择
- 每个步骤可做的选择就是选和不选
- 以深度优先搜索的方式,从第一个物品开始判断,如果当前的选择之后没有超过背包的容量,则记录当前的背包重量,进入下一步选择;如果当前的选择已经超过了背包的容量,或者已经做完了所有的选择,则拿当前的背包重量和最大背包重量比较(刚开始时最大背包重量为0),如果比最大背包重量大,则更新最大背包重量,否则不更新,然后回溯到上一步,继续选择,直到做完所有的选择。
代码实现
public class MaxWeight {
private static int mMaxWeight = 0;
public static int countMax(int[] goods, int max) {
mMaxWeight = 0;
countMax(goods, max, 0, 0);
return mMaxWeight;
}
private static void countMax(int[] goods, int max, int current, int currentWeight) {
if (current == goods.length || currentWeight == max) {//所有商品的选择都做完了或者背包已经装满了
if (currentWeight > mMaxWeight) {
mMaxWeight = currentWeight;
}
return;
}
//不选当前商品
countMax(goods, max, current + 1, currentWeight);
//选择当前商品
if (currentWeight + goods[current] <= max) {//选择当前商品之后,没有超过最大重量
countMax(goods, max, current + 1, currentWeight + goods[current]);
}
}
}
测试用例
@Test
public void test1() {
int max = 100;
int size = 10;
int[] goods = new int[size];
for (int i = 0; i < size; i++) {
goods[i] = new Random().nextInt(max);
}
print(goods, "weights:");
System.out.println("maxWeight:" + MaxWeight.countMax(goods, max));
}
测试结果
weights:87,72,86,2,89,66,88,27,89,74,
maxWeight:99
weights:35,50,59,69,4,44,36,82,46,78,
maxWeight:100
3. 完整源码
完整源码和测试用例请查看github之回溯算法
4. 图片来源
文中图片来源:极客时间,王争《数据结构与算法之美》