1. 是什么
Feature Engineering is the process of transforming raw data into features that better represent the underlying problem to the predictive models,resulting in improved model accuracy on unseen data.(特征工程是将原始数据转换为特征的过程,这些特征能更好地代表预测模型的潜在问题,从而提高不可见数据的模型精度)
特征是数据中抽取出来的对结果预测有用的信息。特征工程就是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥出更好的作用的过程。
举个例子,一个简单的逻辑回归二分类问题。设计一个身材分类器,输入数据X:身高和体重,标签Y:身材(胖/不胖),显然不能根据体重来判断一个人胖不胖,针对这个问题,一个经典的特征工程是:BMI指数,BMI=体重/,大部分人都可以使用BMI指数检测身材标准,这样,通过BMI指数就能非常显然地帮助我们刻画一个人的身材如何。
特征工程其实是一个如何展示和表现数据的问题,在实际工作中需要把数据以“良好”的方式展示出来,使得能够使用各种各样的机器学习模型来得到更好的结果。如何从原始数据中去除不佳的数据,展示合适的数据成了特征工程的关键问题。
特征工程的重要性有以下几点:
特征越好,灵活性越强。好的特征的灵活性在于它允许你选择不复杂的模型,同时运行速度也更快,也更容易和维护。
特征越好,构建的模型越简单。好的特征可以在参数不是最优的情况,依然得到很好的性能,减少调参的工作量和时间,也就可以大大降低模型复杂度。
特征越好,模型的性能越出色。特征工程的目的本来就是为了提升模型的性能。
2. 基本流程
2.1 数据采集、清洗、采样
数据采集前需要明确采集哪些数据,一般思路为:哪些数据对最后的结果预测有帮助?数据能够采集到吗?线上实时计算的时候获取是否快捷?
举例:我现在要预测用户对商品的下单情况,或者我要给用户做商品推荐,那我需要采集什么信息呢?
-店家:店铺的评分、店铺类别…
-商品:商品评分、购买人数、颜色、材质、领子形状…
-用户:历史信息(购买商品的最低价最高价)、消费能力、商品停留时间…
数据清洗就是要去除脏数据。要如何判定脏数据?
- 简单属性判定:一个人身高3米+的人;一个人一个月买了10w的发卡。
-组合或统计属性判定:号称在米国却ip一直都是大陆的新闻阅读用户?你要判定一个人是否会买篮球鞋,样本中女性用户85%?
-补齐可对应的缺省值:不可信的样本丢掉,缺省值极多的字段考虑不用。
数据采样:采集清洗过数据之后,正负样本是不均衡的(什么是正负样本?),要进行数据采样。采样的方法有随机采样、分层采样等,随机采样得到的数据可能会很不均匀,更多的是根据特征采用分层抽样。
正负样本不平衡处理办法:
正样本 >> 负样本,且量都挺大 => downsampling(下采样)
正样本 >> 负样本,量不大 =>
-采集更多的数据
-上采样/oversampling(比如图像识别中的镜像和旋转)
-修改损失函数/loss function (设置样本权重)
2.2 预处理
通过特征提取,我们能得到未经处理的特征,这时的特征还需要进行进一步处理。
2.2.1 去重处理:
对于重复值进行削减
2.2.2 缺失值处理:
可能会出现一些暂时无法获取的信息,被遗漏的信息,不存在属性信息等。
缺失值解决办法:
-直接删除(仅有少量样本缺失时可尝试使用)
-插值补全特征值
a. 均值/中位数/众数补全
均值补全--样本属性可度量
中位数/众数--样本属性距离不可度量
b. 固定数值补全
c. 模型预测
建立一个模型预测缺失的数据。即用其他特征做预测模型,来算出缺失特征,但若缺失特征与其他变量之间没有太大相关,预测结果将会不准确。
d. 高维映射
把特征映射到高维空间。
将属性映射到高维空间,采用独热编码(one-hot)技术。将包含 K 个离散取值范围的属性值扩展为 K+1 个属性值,若该属性值缺失,则扩展后的第 K+1 个属性值置为 1。
这种做法是最精确的做法,保留了所有的信息,也未添加任何额外信息,若预处理时把所有的变量都这样处理,会大大增加数据的维度。这样做的好处是完整保留了原始数据的全部信息、不用考虑缺失值;缺点是计算量大大提升,且只有在样本量非常大的时候效果才好。
2.2.3 数据变换:
单个特征上的规范化、离散化、稀疏化。
a. 规范化处理
也就是数据的归一化和标准化。数据中不同的特征由于量纲往往不同,数值间差距可能非常大,会影响到数据分析的结果。需要对数据按照一定比例进行缩放,保持数据所反映的特征信息的同时,使之落在合理范围内,便于进行综合分析。
常用方法包括:
线性归一化:
非线性数据变换:
对数函数,常用于数据量级非常大的场合。
反正切函数,用于将角频率转换到[-1,1]范围内。
标准化(z-score):,使数据服从标准正态分布
b. 离散化处理
指将连续的数据进行分段,称为离散化的区间。分段的原则有基于等距离、等频率等方法。
离散化的原因是因为一些模型是基于离散的数据的,如决策树。有效的离散化能减少算法的空间时间开销,提高系统对样本的分类聚类能力和抗噪声能力。
c. 稀疏化处理
对于离散型类别标签数据,通常将其做0、1哑变量的稀疏化。尤其将原始字符串心事的数据数值化。除了决策树等少量模型能直接处理字符串输入,对于逻辑回归、SVM等来说,数值化处理是必须的。
如果特征的不同值较多,则根据频数,所有出现次数较少的值可以归为同一类。
一般采用的方法有Ordinal Encoding、One-hot Encoding、Binary Encoding。
2.3 特征选择
在训练机器学习模型之前,特征选择是一个很重要的预处理过程,之所以进行特征选择,原因有:
-现实任务中经常遇到维数灾难问题,如果能选择出重要特征,再进行后续学习过程,可以减轻维数灾难;
-去除不相关的特征往往会降低学习任务的难度,使模型更易理解;
-去除不相关的变量还可以尽量减少过拟合的风险,尤其是在使用人工神经网络或者回归分析等方法时,额外的输入变量会增加模型本身的额外自由度。
2.3.1 两个关键环节
想要从初始的特征集合中选取一个包含所有重要信息的特征子集,若没有任何先验知识,则只可能遍历所有可能的子集,然而这样在计算上显然不可能,尤其是在特征个数很多的情况下。
可行的办法是,产生一个候选子集,评价它的好坏,基于评价结果产生下一个候选子集,再对其进行评价...持续这一环节,直到找不到更好的子集为止。这一过程涉及两个关键环节,即如何根据评价结果获取下一个特征子集?以及如何评价候选特征子集的好坏?
1)子集搜索问题
-前向搜索:逐渐增加相关特征的策略。给定特征集合a1,a2,...,an,首先选择一个最优的单特征子集(比如a2)作为第一轮选定集,然后在此基础上加入一个特征,构建包含两个特征的候选子集,选择最优的双特征子集作为第二轮选定子集,依次类推,直到找不到更优的特征子集才停止。
-后向搜索:逐渐减少特征的策略。类似的,如果从完整的特征集合开始,每次尝试去掉一个无关特征。
-双向搜索:前后向搜索结合起来,每一轮逐渐增加选定相关特征(这些特征在后续轮中确定不会被去除),同时减少无关特征。
2)子集评价问题
确定了搜索策略,接下来就需要对特征子集进行评价,以离散属性的信息增益为例,给定数据集D,假定 D 中第 i类样本的比例为 pi(i=1,2,…,n),则信息熵的定义为:
对于属性子集 A,假定根据其取值将 D 成了 V个子集 D1,D2,…,DV,每个子集的样本在 A上取值相同,于是我们可以计算属性子集 A的信息增益为:
信息增益越大,意味着特征子集 A包含的有助于分类的信息越多。于是,对于每个特征子集,我们可以基于训练集 D来计算其信息增益,以此作为评价标准。特征子集搜索机制和子集评价机制相结合,就可以得到特征选择方法。例如,将前向搜索和信息熵相结合就和决策树算法非常相似。
2.3.2 常见的特征选择方法
1)Filter(过滤式)
按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。通过卡方检验、皮尔逊相关系数、互信息等指标判断哪些维度重要,剔除不重要的维度。与学习器无关。
2)Wrapper(包裹式)
使用一个基模型进行多轮训练,每次选择若干特征,或者排除若干特征。根据目标函数(通常是预测效果评分),来决定各特征是否重要。通常结合遗传算法或模拟退火算法等搜索方法来对选取特征。
3)Embedding(嵌入式)
该方法基于机器学习的算法和模型进行训练,学习器通过训练自动对特征进行选择。如使用L1范数作为惩罚项的线性模型(例如lasso回归)会得到稀疏解,大多数特征对应的系数为0。从而实现了特征选择。
2.4 降维
当特征选择完成后,可以直接训练模型了,但是可能由于特征矩阵过大,导致计算量大,训练时间长的问题,因此降低特征矩阵维度也是必不可少的。
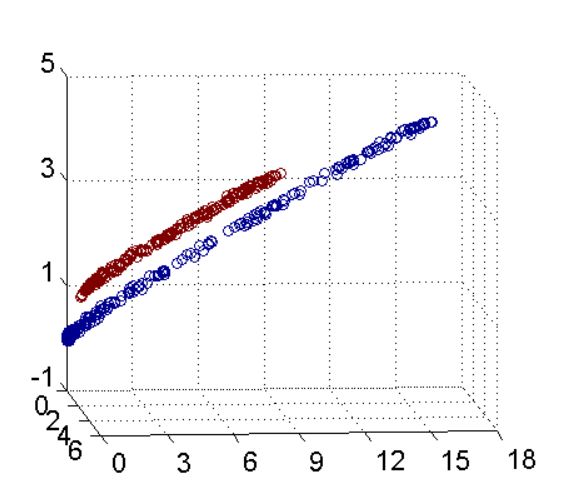
LDA(线性判别分析)与PCA(主成分分析)都是常用的降维方法,二者的区别在于:
-出发思想不同。PCA主要是从特征的协方差角度,去找到比较好的投影方式,即选择样本点投影具有最大方差的方向( 在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。);而LDA则更多的是考虑了分类标签信息,寻求投影后不同类别之间数据点距离更大化以及同一类别数据点距离最小化,即选择分类性能最好的方向。
-学习模式不同。PCA属于无监督式学习,因此大多场景下只作为数据处理过程的一部分,需要与其他算法结合使用,例如将PCA与聚类、判别分析、回归分析等组合使用;LDA是一种监督式学习方法,本身除了可以降维外,还可以进行预测应用,因此既可以组合其他模型一起使用,也可以独立使用。
-降维后可用维度数量不同。LDA降维后最多可生成C-1维子空间(分类标签数-1),因此LDA与原始维度N数量无关,只有数据标签分类数量有关;而PCA最多有n维度可用,即最大可以选择全部可用维度。
如上图,PCA所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上,映射时没有利用任何数据内部的分类信息。因此,虽然PCA后的数据在表示上更加方便(降低了维数并能最大限度的保持原有信息),但在分类上也许会变得更加困难;上图右侧是LDA的降维思想,可以看到LDA充分利用了数据的分类信息,将两组数据映射到了另外一个坐标轴上,使得数据更易区分了(在低维上就可以区分,减少了运算量)。
2.5 总结
特征选择和降维都是为了减少特征的数量。但是特征选择是从原有特征中进行选择或排除,不涉及原有特征的转变;而降维是创造特征的新组合。