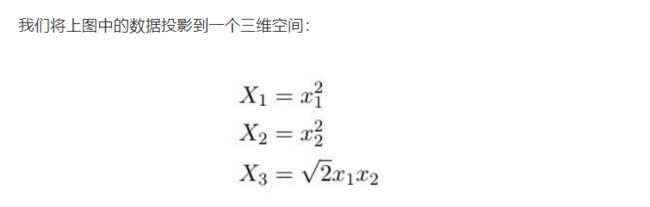Support Vector Machines
scikit-learn中SVM的算法库分为两类,一类是分类的算法库,包括SVC, NuSVC,和LinearSVC 3个类。另一类是回归算法库,包括SVR, NuSVR,和LinearSVR 3个类。相关的类都包裹在sklearn.svm模块之中。
我们使用这些类的时候,如果有经验知道数据是线性可以拟合的,那么使用LinearSVC去分类 或者LinearSVR去回归,它们不需要我们去慢慢的调参去选择各种核函数以及对应参数, 速度也快。如果我们对数据分布没有什么经验,一般使用SVC去分类或者SVR去回归,这就需要我们选择核函数以及对核函数调参了。
什么特殊场景需要使用NuSVC分类 和 NuSVR 回归呢?如果我们对训练集训练的错误率或者说支持向量的百分比有要求的时候,可以选择NuSVC分类 和 NuSVR 。它们有一个参数来控制这个百分比。
nu代表训练集训练的错误率的上限,或者说支持向量的百分比下限,取值范围为(0,1],默认是0.5.它和惩罚系数C类似,都可以控制惩罚的力度。
一般情况下,对非线性数据使用默认的高斯核函数会有比较好的效果,如果你不是SVM调参高手的话,建议使用高斯核来做数据分析。
如果我们在kernel参数使用了多项式核函数 'poly',高斯核函数‘rbf’, 或者sigmoid核函数,那么我们就需要对这个参数进行调参。
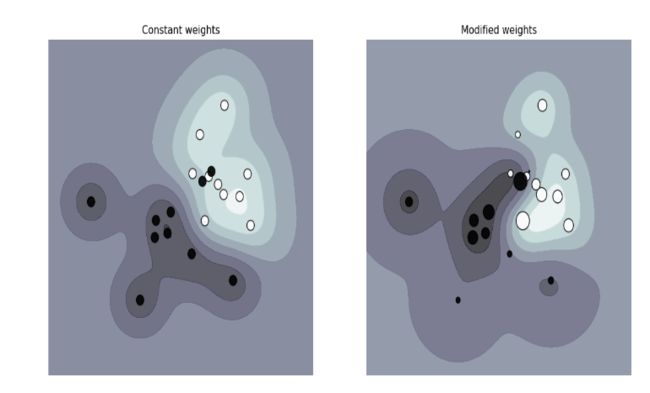
样本权重class_weight:
指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多,导致训练的决策过于偏向这些类别。这里可以自己指定各个样本的权重,或者用“balanced”,如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。当然,如果你的样本类别分布没有明显的偏倚,则可以不管这个参数,选择默认的"None"
首先,常用的核函数有:线性核函数、多项式核函数、(高斯)RBF径向基核函数。
在 SVM 中,选择线性核函数和径向基核函数时,需要对数据进行归一化处理。
一般性建议,高维数据(数据维度大,是或者可以视为线性可分)的情况下,选择线性核函数,不行换特征,再不行换高斯核。
维度少的时候,如果可以的话提取特征使用线性核函数,不行再换高斯核函数,因为线性核函数最简单最快,高斯核复杂而慢,但是除了速度之外的性能一般都可以达到或优于线性核的效果。多项式核的参数比高斯核的多,参数越多模型越复杂;高斯核的输出值域在 0-1之间,计算方便;多项式核的输出值域在 0-inf 在某些情况下有更好的表现。
###
所谓的核技巧,就是使用一个变换将原空间的数据映射到新空间,在新空间里使用线性方法求解。
###
基本思想介绍
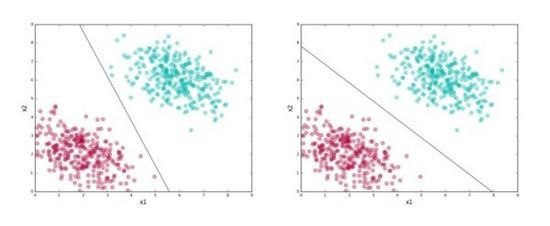
这里有一个有趣的问题:上面的两条线都分开了红色聚类和绿色聚类。是否有很好的理由选择一条,不选择另一条呢?
别忘了,分类器的价值不在于它多么擅长分离训练数据。我们最终想要用它分类未见数据点(称为 测试数据)。因此,我们想要选择一条捕捉了训练集中的 通用模式(general pattern)的线,这样的线在测试集上表现出色的几率很大。
上面的第一条线看起来有点“歪斜”。下半部分看起来太接近红聚类,而上半部分则过于接近绿聚类。是的,它完美地分割了训练数据,但是如果它看到略微远离其聚类的测试数据点,它很有可能会弄错标签。
第二条线没有这个问题。第二条线在正确分割训练数据的前提下,尽可能地同时远离两个聚类。保持在两个聚类的正中间,让第二条线的“风险”更小,为每个分类的数据分布留出了一些摇动的空间,因而能在测试集上取得更好的概括性。
SVM试图找到第二条线。上面我们通过可视化方法挑选了更好的分类器,但我们需要更准确一点地定义其中的理念,以便在一般情形下加以应用。下面是一个简化版本的SVM:
1、找到正确分类训练数据的一组直线。
2、在找到的所有直线中,选择那条离最接近的数据点距离最远的直线。
支持向量是怎么计算的
距离最接近的数据点称为 支持向量(support vector)。
支持向量定义的沿着分隔线的区域称为 间隔(margin) 。
尽管上图显示的是直线和二维数据,SVM实际上适用于任何维度;在不同维度下,SVM寻找类似二维直线的东西。
SVM允许我们通过参数 C 指定愿意接受多少误差。
由于现实世界的数据几乎从来都不是整洁的,因此决定较优的C值很重要。我们通常使用 交叉验证(cross-validation)之类的技术选定较优的C值。
核函数
注意,关键的地方来了!我们已经有了一项非常擅长寻找超平面的技术,但是我们的数据却是非线性可分的。所以我们该怎么办? 将数据投影到一个线性可分的空间,然后在那个空间寻找超平面!
2. 所以我首先投影数据接着运行SVM?
否。为了让上面的例子易于理解,我首先投影了数据。其实你只需让SVM为你投影数据。这带来了一些优势,包括SVM将使用一种称为 核(kernels)的东西进行投影,这相当迅速(我们很快将讲解原因)。
另外,还记得我在上一点提过投影至无穷维么?那该如何表示、存储无穷维呢?结果SVM在这一点上非常聪明,同样,这和核有关。
这是让SVM奏效的秘密武器。这里我们需要一点数学。
让我们回顾下之前的内容:
SVM在线性可分的数据上效果极为出色。使用正确的C值,SVM在基本线性可分的数据上效果相当出色。线性不可分的数据可以投影至完美线性可分或基本线性可分的空间,从而将问题转化为1或2.
看起来让SVM得到普遍应用的关键是投影到高维。这正是核的用武之地。
SVM的目标是在正确分类的前提下,最大化间隔宽度
你可以不用在意以上公式的细节,只需注意一点, 以上计算都是基于向量的内积。也就是说,无论是超平面的选取,还是确定超平面后分类测试数据点,都只需要计算向量的内积。
而 核函数(kernel function),简称 核(kernel) 正是算内积的!核函数接受原始空间中两个数据点作为输入,可以 直接给出投影空间中的点积。
看来用核函数计算所需内积要快得多。大型数据集上,核函数节省的算力将飞速累积。这是核函数的巨大优势。
大多数SVM库内置了流行的核函数,比如 多项式(Polynomial)、 径向基函数(Radial Basis Function,RBF) 、 Sigmoid 。当我们不进行投影时(比如本文的第一个例子),我们直接在原始空间计算点积——我们把这叫做使用 线性核(linear kernel) 。
我们通常并不定义数据的投影。相反,我们从现有的核中选取一个,加以微调,以找到最匹配数据的核函数。我们当然可以定义自己的核,甚至自行投影。但许多情形下不必如此。至少,我们从尝试现有核函数开始。如果存在我们想要的投影的核,我们将使用它,因为核经常快很多。RBF核可以投影数据点至无穷维。
事实上,如果你需要 快速了解不同核、C值等对寻找分割边界的影响,你可以尝试libSVM主页上的“图形界面”。标记数据点分类,选择SVM参数,然后点击运行(Run)!这个可视化工具的魅力无可阻挡
参考文献
【1】https://www.cnblogs.com/pinard/p/6117515.html scikit-learn 支持向量机算法库使用小结
【2】https://baijiahao.baidu.com/s?id=1607469282626953830&wfr=spider&for=pc SVM教程:支持向量机的直观理解
【3】https://blog.csdn.net/qq_35992440/article/details/80987664 SVM支持向量机入门及数学原理
【4】https://blog.csdn.net/MachineRandy/article/details/80358931 机器学习中的核技巧