数据结构与算法之图(一)图的构建与遍历(邻接矩阵法)

引言

图是一种比线性表和树更复杂的数据结构，在图中，结点之间的关系是任意的，任意两个数据元素之间都可能相关。图是一种多对多的数据结构。它包含顶点集合和边集合两部分，边反映了顶点之间的关系。具体定义如下:
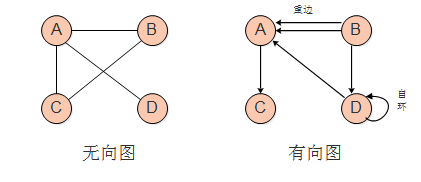
图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V，E），其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。图可以没有边，但是必须有顶点。根据边是否存在方向，我们将图分为有向图和无向图，结构如下:

有关图的其他术语如边的权重、顶点的度等等概念请字形查阅，这里不再赘述。

图的存储结构

图的常用存储结构有:邻接矩阵法和邻接表法：
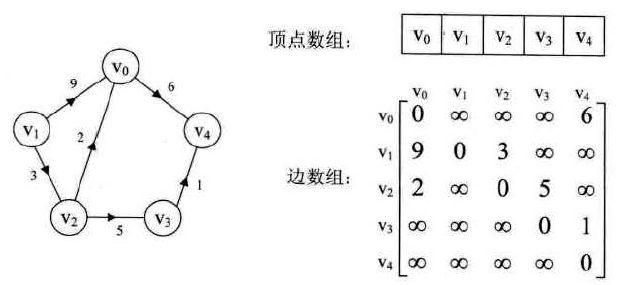
1.邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称邻接矩阵）存储图中的边或弧的信息。结构图如下:

邻接矩阵

下面就是具体的例子:

有向图邻接矩阵例子

二维数组元素adj[i][j]的下标及对应的权重反映了顶点i与j的关系:adj[i][j]权重有效时(大于0且不是无穷)，表示从i顶点可以到达j顶点;本节点相对本节点的权重为0;权重为无穷表示顶点没有单向没有连接。可以看出，两个数组几乎反映了图的所有信息，这种方法结构简单，易于操作，但是对于稀疏图，会造成空间巨大浪费。
2.邻接表是一种将数组与链表相结合的存储方法。每一个数组元素存放一个单链表，单链表里面存的是与头结点相邻的顶点。结构图如下:

图的邻接表描述

邻接表引入单链表，操作相对复杂，查找效率相对较低，适合稀疏图。本文先学习相对简单的邻接矩阵法作为入门，来熟悉图的基本操作。

图的邻接矩阵描述

/**
 * Created by chenming on 2018/6/15
 */
public class MatrixGraph {
    private int[][] weightEdges;//带权重边二维数组，weightEdges[i][j]表示节点i到j的权重
    private int[] vertexes;//顶点数组
    public static int NO_WEIGHT_VALUE = Integer.MAX_VALUE;

    public MatrixGraph(int[] vertexes, int[][] edges) {
        if (vertexes == null || edges == null || vertexes.length != edges.length) {
            return;
        }
        this.vertexes = vertexes;
        this.weightEdges = edges;
    }
    ...
}

二维数组weightEdges存放边信息，反映顶点之间的连接情况，vertexes为顶点数组，简单起见，这里用整数代替泛型。

图的遍历

从图的某个顶点出发，遍历图中其余顶点，且使每个顶点仅被访问一次，这个过程叫做图的遍历。类似于我们搜索房间，它的遍历通常有两种方法：深度优先遍历和广度优先遍历。

图的深度优先遍历

类似于树的前序遍历，图的深度遍历为纵向遍历，步骤如下:
1.先访问顶点V，在访问它的相邻顶点W,然后在访问W的相邻顶点X..直到最深的相邻顶点被访问过或者到达路径底部,递归过程结束。
2.若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。
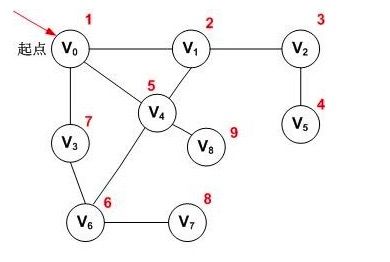
下图是一个深度优先遍历的实例:

图的深度优先遍历.png

红色数字代表遍历的先后顺序，它的深度优先遍历的顶点访问序列为：V0，V1，V2，V5，V4，V6，V3，V7，V8。
实现代码如下:

 /**
     * 深度优先遍历
     */
    public void transverseDfs() {
        boolean[] isAccessedTable = new boolean[vertexes.length];
        //初始化访问标记数组
        for (int i = 0; i < vertexes.length; i++) {
            isAccessedTable[i] = false;
        }

        for (int i = 0; i < vertexes.length; i++) {
            if (!isAccessedTable[i]) {
                //递归深度优先遍历
                dfsVertexes(i, isAccessedTable);
            }
        }
    }

    /**
     * 递归深度遍历顶点
     *
     * @param index           顶点索引
     * @param isAccessedTable
     */
    private void dfsVertexes(int index, boolean[] isAccessedTable) {
        isAccessedTable[index] = true;//访问节点
        System.out.println("深度优先遍历:" + vertexes[index]);//访问节点
        for (int i = 0; i < vertexes.length; i++) {
            //没有访问，且为连接顶点则递归遍历
            int temp = weightEdges[index][i];
            if (!isAccessedTable[i] && temp > 0 && temp < Integer.MAX_VALUE) {
                dfsVertexes(i, isAccessedTable);
            }
        }
    }

图的广度优先遍历

广度优先遍历类似于二叉树的层序遍历,它的基本思路是:
1.先访问出发点V[i]，标记V[i]访问过;
2.访问V[i]的未被访问过的相邻顶点，并标记它们;
3.对于V[i]的相邻顶点，重复执行2步骤。
示意图如下:

图的广度优先遍历.png

采用广度优先搜索遍历以V0为出发点的顶点序列为：V0，V1，V3，V4，V2，V6，V8，V5，V7。
这里我们和二叉树的层序遍历思想一样，引入队列存放下一层将要遍历的顶点，每一次迭代，都从队列头取顶点V[i]，然后将V[i]的相邻未访问节点V[i][x]集合加入到队列，直到队列为空，这样就保证的层的访问顺序。具体实现代码如下:

    /**
     * 广度遍历和二次树的层序遍历相似,引入队列，存放当前未访问的连接节点
     */
    public void transverseBfs() {
        boolean[] isAccessedTable = new boolean[vertexes.length];
        for (int i = 0; i < vertexes.length; i++) {
            isAccessedTable[i] = false;
        }
        Integer headIndex;
        Queue queue = new Queue<>();//也可以用LinkList代替
        for (int i = 0; i < vertexes.length; i++) {//各顶点作为入口
            if (!isAccessedTable[i]) {
                headIndex = i;//层序遍历起点
                while (headIndex != null) {//一次层序遍历,直到遍历完最后一层，队列为空
                    isAccessedTable[headIndex] = true;//遍历当前节点
                    System.out.println("广度优先遍历:" + vertexes[headIndex]);
                    //查找未访问的连接点入队
                    for (int j = 0; j < vertexes.length; j++) {
                        int tmp = weightEdges[headIndex][j];
                        if (!isAccessedTable[j] && tmp > 0 && tmp < Integer.MAX_VALUE && !queue.contains(j)) {
                            //未访问的连接点j入队
                            queue.enquene(j);
                        }
                    }
                    headIndex = queue.dequeue();//取未访问的节点
                }
            }
        }
    }

测试代码:

    @Test
    public void testGraph() {
        /**
         * 图的邻接矩阵描述
         */
        int[] vertexes = new int[]{
                0, 1, 2, 3, 4

        };

        int[][] edges = new int[][]{
                new int[]{0, MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, 6},
                new int[]{9, 0, 3, MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE},
                new int[]{2, MatrixGraph.NO_WEIGHT_VALUE, 0, 5, MatrixGraph.NO_WEIGHT_VALUE},
                new int[]{MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, 0, 1},
                new int[]{MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, MatrixGraph.NO_WEIGHT_VALUE, 0},
        };
        MatrixGraph graph = new MatrixGraph(vertexes, edges);
        System.out.println("邻接矩阵深度优先遍历:");
        graph.transverseDfs();
        System.out.println("邻接矩阵广度优先遍历:");
        graph.transverseBfs();
    }

测试结果:

邻接矩阵深度优先遍历:
深度优先遍历:0
深度优先遍历:4
深度优先遍历:1
深度优先遍历:2
深度优先遍历:3
邻接矩阵广度优先遍历:
广度优先遍历:0
广度优先遍历:4
广度优先遍历:1
广度优先遍历:2
广度优先遍历:3

本篇介绍了图的邻接矩阵构建及遍历方法,它的应用主要有:最短路径规划、最小生成树和拓扑排序，后面再学习它们的实现。
完整代码地址:数据结构与算法学习JAVA描述GayHub地址