数据结构与算法学习笔记(3):图解数据结构与算法-复杂度分析(二):常见复杂度分析
立即学习:https://edu.csdn.net/course/play/29510/420448?utm_source=blogtoedu
复杂度分析(二)常见复杂度分析
三种分析方法
- 单段代码看高频:只关注循环执行次数最多的一段代码
- 多段代码取最大:总复杂度等于量级最大的那段代码的复杂度
- 嵌套代码求乘积:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
【例1】
(伪)代码:
sum = 0;
for(i=1; i<=n; i++){
sum = sum + (-1)^n;
}分析:
每行代码所需要的unit_time
第一行:1 * unit_time
第二行:n * unit_time
第三行:n * unit_time
一共需要:(2n + 1) * unit_time结论:只关注循环执行次数最多的一段代码——单段代码看高频
大O统计法
T(n)=O(2n+1)
求极限后
T(n)=O(n)
【例2】
(伪)代码:
sum_1 = 0;
for(p = 1; p<=100; ++p){
sum_1 = sum_1 + p;
}
sum_2 = 0;
for(q = 1; q<=n; ++q){
sum_2 = sum_2 + q;
}
sum_3 = 0;
for(i = 1; i<=n; ++i){
for(j = 1; j < n; ++j){
sum_3 = sum_3 + i * j;
}
}
return sum_1 + sum_2 + sum_3;分析:
每行代码执行需要unit_time
第一段:(1 + 100 + 100) * unit_time [常数项]
第二段:(2n + 1) * unit_time [一次项]
第三段:(2n^2 + n + 1) * unit_time [二次项]结论:多段代码取最大
多段代码时
T1(n) = O(f(n)), T2(n) = O(g(n))
T(n) = T1(n) + T2(n)
= max(O(f(n)), O(g(n)))
= O(max(f(n), g(n)))
这个代码中 2n^2 + n + 1的量级更大
因此
T(n) = O(2n^2 + n + 1)
求极限得
T(n) = O(n^2)
【例3】
(伪)代码:
sum = 0;
sub1{
for(i=1; i<=n; i++){
sub2;
}
}
sub2{
for(j = 1; j<=n; j++){
for(k=1; k<=n; k++){
sum = sum +j;
}
}
}分析:
每行代码需要的unit_time
sub1: (n + n*sub2) * unit_time
sub2: (n + n^2 + n^2) * unit_time
总: (1 + n + n * (n + n^2 + n^2)) * unit_time
= (1 + n + n^2 + 2n^3) * unit_time结论:嵌套代码求乘积
大O统计法
T(n) = O(1+n+n^2+2n^3)
求极限
T(n) = O(n^3)
算然代码千差万别,但是涵盖的复杂量级并不多。
常见复杂量级如下:
非多项式量级的算法问题叫做NP问题,即为非确定多项式(Non_Deterministic Polynomial);
当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。
常见的多项式时间复杂度:
O(1):
O(1)只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。
只要代码的执行时间不随n的增大而增长,这样的代码的时间复杂度我们都记作O(1)
或者说,一般情况下,只要算法中不存在循环语句,递归语句,即使有千万行代码,其时间复杂度也是O(1)
【例】
O(m + n) / O(m * n)
针对于不同的代码块:代码中出现两段执行次数不同的,但是不确定谁大谁小, 不确定谁的影响力比较高
【例】
原来的加法法则就不正确了,我们需要将加法规则改为:
T1(m) + T2(n) = O(f(m) + g(n))
但是乘法法则继续有效:
T1(m) * T2(n) = O(f(m) * f(n))
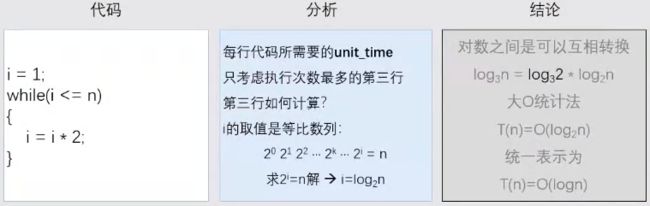
O(logn) / O(nlogn)
对数阶时间复杂度非常常见,同时也是最难分析的一种时间复杂度
如果一段代码的时间复杂度是O(logn), 我们循环执行n遍,时间复杂度就是O(nlogn)
【例】