【学习笔记】李宏毅2021春机器学习课程第2.4节:Batch Normalization(批标准化)
文章目录
-
-
- 1 解决提出问题的人——改变 error surface
- 2 特征标准化
- 3 考虑深度学习的情况
- 4 考虑 Batch Normalization在测试集中的问题
- 5 Batch Normalization 确实能帮助我们更好地训练神经网络
- 6 Batch Normalization 究竟为什么会有帮助呢?
- 附录:其他的标准化方法
-
到目前为止我们讲的都是当我们的error surface非常崎岖的时候,应该怎么样来做optimization,来让我们的训练可以继续下去,但是这种崎岖的error surface让我们在调参的过程中很痛苦。
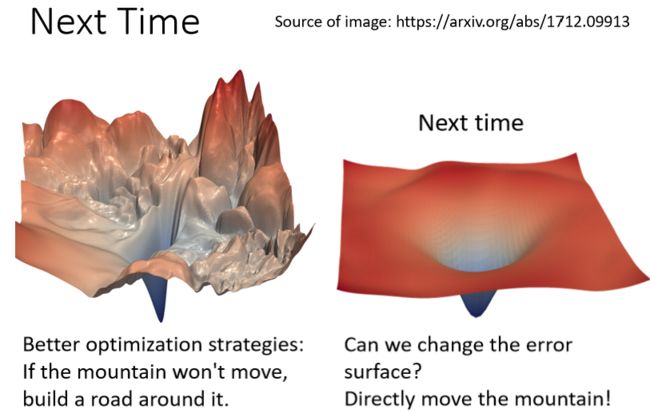
那么既然解决问题很难,那我们能不能解决提出问题的人呢(x)
也就是说,我们有没有可能把这个崎岖的error surface变得正常一点,变得容易训练一点,这就是接下来我们要讨论的东西。
1 解决提出问题的人——改变 error surface
Batch Normalization就是其中一个把崎岖的error surface变平滑的想法。
Batch Normalization,批标准化,和普通的数据标准化类似,是将分散的数据统一的一种做法, 也是优化神经网络的一种方法,具有统一规格的数据, 能让机器学习更容易学习到数据之中的规律。
之前就提到过,不要小看 optimization 这个问题,有时候就算你的error surface就是一个碗的形状,也不见得就很好训练。
假设你的现在有一个模型的error surface如下所示,它的两个参数分别是 w 1 w_1 w1和 w 2 w_2 w2,假设 w 1 w_1 w1是横轴方向, w 2 w_2 w2是纵轴方向,那么你可以看到这两个参数对 Loss 的斜率差别非常大,在 w 1 w_1 w1 这个方向上面斜率变化很小,在 w 2 w_2 w2 这个方向上面斜率变化很大。
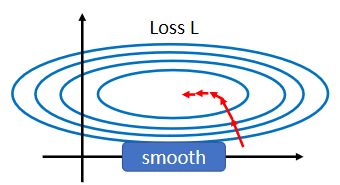
如果是固定的 learning rate,你可能很难得到好的结果,这也正是我们上一节提出adaptive learning rate的原因。但现在我们要试着从另一个角度来解决问题,直接把不好训练的 error surface 改掉,看能不能够改得好做一点。
在做这件事之前,也许我们第一个要问的问题就是,这种 w 1 w_1 w1 跟 w 2 w_2 w2 的斜率差很多的状况到底是怎么出现的。
还是用一个例子来说明这件事,假设我们现在有一个非常简单的 linear model,没有 activation function,它的输入是 x 1 x_1 x1 跟 x 2 x_2 x2,它对应的参数是 w 1 w_1 w1 跟 w 2 w_2 w2,如下所示:

w 1 w_1 w1 乘 x 1 x_1 x1, w 2 w_2 w2 乘 x 2 x_2 x2 ,再加上 b 以后就得到 y,然后会计算 y 跟 y ^ \hat{y} y^ 之间的差距当做 e,把所有 training data 的 e 加起来就得到Loss。
那在怎样的状况下我们会产生像上面那样比较不好 train 的 error surface 呢?
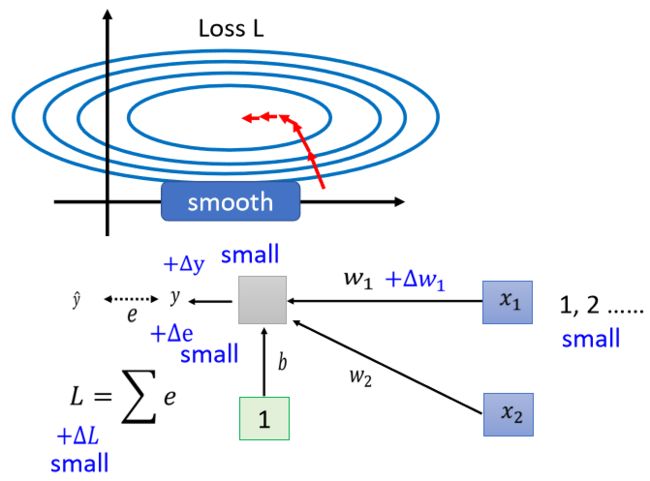
当我们对 w 1 w_1 w1 有一个小小的改变,比如说加上 d e l t a delta delta w 1 w_1 w1 的时候,输出的y就会改变,而y的改变又会导致e的改变,最终导致改变了L。这时我们可能会发现,**由于 x 1 x_1 x1 会直接乘上 w 1 w_1 w1,**在 d e l t a delta delta w 1 w_1 w1 不变的情况下,如果 x 1 x_1 x1本身的数量级很大,那么算出的 d e l t a delta delta L L L就很大, w 1 w_1 w1在 error surface 上的斜率就大;如果 x 1 x_1 x1本身的数量级很小,那么算出的 d e l t a delta delta L L L就很小, w 1 w_1 w1在 error surface 上的斜率就小。

所以我们发现在这个 linear 的 model 里面,当我们 input 的 feature,每一个 dimension 的 scale 差距很大的时候,我们就可能产生不同方向坡度非常不同的 error surface。所以一个很自然的想法是:如果我们可以让不同的dimension拥有同样的scale的话,那我们就有可能产生比较容易训练的error surface。这个想法的实现方法就是接下来要提到的Feature Normalization。

2 特征标准化
以下所讲的方法只是 Feature Normalization 的一种可能性,并不是 Feature Normalization 的全部,假设 x 1 x^1 x1 到 x R x^R xR是我们所有的训练资料的 feature vector。
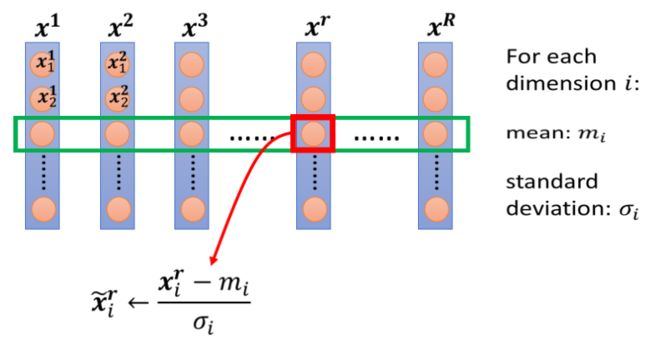
我们把不同笔资料即不同 feature vector的同一个 dimension 里的数值全部取出来(在图中以第i行为例),然后去计算这些数值的平均值 m i m_i mi,再计算它们的标准差 σ i \sigma_i σi,接下来我们来做normalization (也叫standardization):
x ~ i r ← x i r − m i σ i \tilde{x}^r_i ← \frac{x^r_i-m_i}{\sigma_i} x~ir←σixir−mi
得到新的数值叫做 x ~ \tilde{x} x~,再用新的数值替换原来位置上的数值。
那做完 normalize 以后有什么好处呢?

- 做完 normalize 以后,这个 dimension 上面数值的平均值为 0,方差为1,所以这一排数值的分布就都会在 0 上下。
- 对每一个 dimension都做一样的 normalization,就会发现所有 feature 不同 dimension 的数值都在 0 上下,这样就更可能产生比较容易训练的error surface
3 考虑深度学习的情况
网络的输入经过我们的feature normalization处理之后,数值的分布就很相近了,但在经过网络的第一层之后,也就是这边得到的 a 1 a^1 a1 a 2 a^2 a2 a 3 a^3 a3 ,又需要作为下一层的输入,而对于下一层来说,这里的 a 1 a^1 a1 a 2 a^2 a2 a 3 a^3 a3的数值的分布仍然可能又有了很大的差异。对 w 2 w_2 w2 来说,这边的 a 或 z 其实也是一种 feature,我们应该要对这些 feature 也做 normalization。

那如果你选择的激活函数是 Sigmoid,那可能比较推荐对 z 做 Feature Normalization,因为Sigmoid是一个 s 的形状,它在 0 附近斜率比较大,所以如果你对 z 做 Feature Normalization,把所有的值都挪到 0 附近,那你到时候算 gradient 的时候,算出来的值会比较大,模型就比较好训练。但总体而言,这个 normalization放在 activation function 之前或之后都是可以的,实际上并没有太大的差别。

接下来你可能会注意到一件有趣的事情,在我们没有对 z z z 做Feature Normalization的时候,如果你改变了 z 1 z^1 z1 的值,你只会影响到后面 a 1 a^1 a1的值。
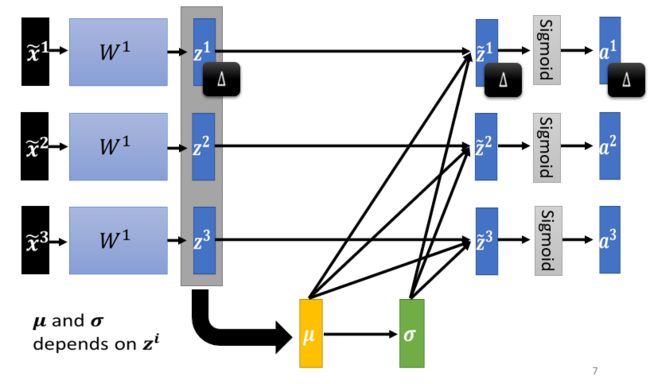
但是现在呢,这边的 μ μ μ 跟 σ \sigma σ,它们其实都是根据 z 1 z^1 z1 z 2 z^2 z2 z 3 z^3 z3 算出来的,当你改变 z 1 z^1 z1 的值的时候, μ μ μ 跟 σ \sigma σ 也会跟着改变, μ μ μ 跟 σ \sigma σ 改变以后, a 1 a^1 a1 a 2 a^2 a2 a 3 a^3 a3的值都会跟着改变。
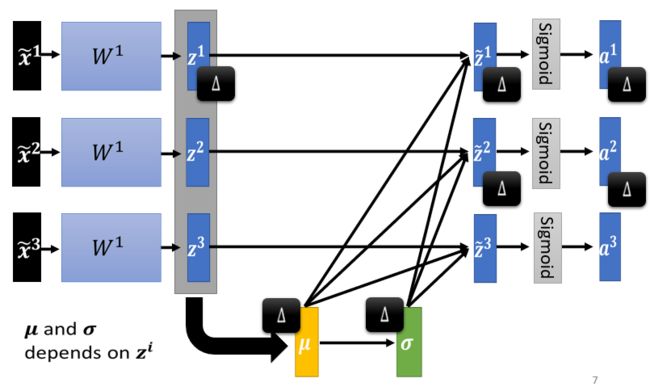
所以之前,我们每一个 x ~ 1 \tilde{x}_1 x~1 x ~ 2 \tilde{x}_2 x~2 x ~ 3 \tilde{x}_3 x~3,都是独立分开处理的,但是我们在做 Feature Normalization 以后,这三个值却变得彼此关联了,整个系统成为了一个比较大的network。
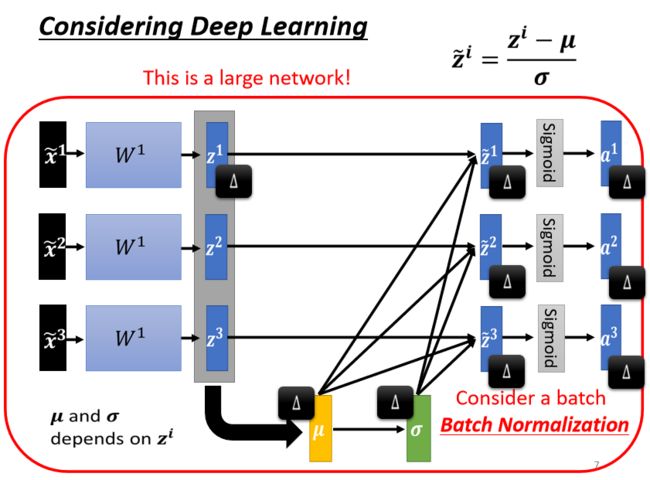
接下来就会有一个问题了,因为你的训练资料里面的 data 非常多,现在一个 data set 动不动就有上百万笔资料, GPU 的 memory 根本没有办法把整个 data set 的 data 都 load 进去。
所以在实践过程中,我们不会让这一个 network 考虑整个 training data 里面的所有 data,我们只考虑一个 batch 里面的 data,举例来说,batch size 设为 64,那这个巨大的 network,就是把 64 笔 data 读进去,算这 64 笔 data 的 μ μ μ,算这 64 笔 data 的 σ \sigma σ,对这 64 笔 data 都去做 normalization。这就是Batch Normalization名字的由来。
但这里又有另一个问题,就是我们一定要有一个够大的 batch,你才算得出比较有用的 μ μ μ 跟 σ \sigma σ,举个极端一点的例子,假如我们的 batch size 设为 1,那你其实就没有什么 μ μ μ 或 σ \sigma σ 可以算,也没什么意义。换句话说,这里的 μ μ μ 跟 σ \sigma σ是两个统计量,我们在一个batch上统计这两个量,希望它能够代表整个data set的情况,所以你的batch一定不能太小,不然就不具有代表性。
在做 Batch Normalization 的时候,往往还会有这样的设计,在你算出这个 z ~ \tilde{z} z~ 以后:
- 接下来你会把这个 z ~ \tilde{z} z~再乘上另外一个向量叫做 γ γ γ,就是把 z ~ \tilde{z} z~这个向量里面的 element,跟 γ γ γ 这个向量里面的 对应位置的element两两做相乘。
- 最后再加上 β β β 这个向量,得到 z ^ \hat{z} z^。
这里的 β β β 跟 γ γ γ,可以把它想成是 network 的参数,它们是另外再被learn出来的。

那为什么要加上 β β β 跟 γ γ γ 呢?这是因为有人觉得如果我们做 normalization 以后, z ~ \tilde{z} z~它的平均就一定是 0,这就给了 network 一些限制,也许这个限制会带来一些负面的影响,所以我们把 β β β 跟 γ γ γ 加回去,就可以让我们的network自己学习这两个参数,来调整输出的分布。
但这里又会有一个疑问,刚刚做 Batch Normalization 不就是为了要让每一个不同的 dimension,它的 range 都相同吗,现在如果加去乘上 γ γ γ,再加上 β β β,把 γ γ γ 不就又会导致 range 不一样了吗。
这件事是有可能发生的,但是你实际上在训练的时候,这个 γ γ γ 的初始值是全为1的向量, β β β 的初始值是全为0的向量,这样你的 network 在一开始训练的时候,每一个 dimension 的数值范围仍然是比较接近的,在你已经训练够长的一段时间,已经找到一个比较好的 error surface之后,再把 γ γ γ 跟 β β β 慢慢地加进去,这样总体上仍然对你的训练是有帮助的。
4 考虑 Batch Normalization在测试集中的问题
上面所说的都是 Batch Normalization 在training的时候相关的一些问题,现在我们来看看testing的时候。
在testing的时候,一个比较明显的问题体现在实际应用中,假设你真的有系统上线,是一个真正的线上的 application,你的资料是一笔一笔逐步获取的,如果你的 batch size 设为 64,一定要等 64 笔资料都进来,才去一次做运算吗,这显然是不行的。
在 testing 的时候,如果 当然如果今天你是在做作业,我们一次会把所有的 testing 的资料给你,所以你确实也可以在 testing 的资料上面,製造一个一个 batch

但是在做 Batch Normalization 的时候,之前也提到过这个 μ μ μ 跟 σ \sigma σ,是用一个 batch 的资料算出来的,而且这个batch还不能太小,不然就不具有代表性。但我们现在的问题是在testing的时候,起初连一个batch的资料都还没有收集到,要怎么算这个 μ μ μ 跟 σ \sigma σ呢?
我们的解决方案是:在training的时候,每一个batch计算出来的 μ μ μ 跟 σ \sigma σ分别算moving average μ ˉ \barμ μˉ 跟 σ ˉ \bar\sigma σˉ ,之后的testing直接使用这个 μ ˉ \barμ μˉ 跟 σ ˉ \bar\sigma σˉ 来替代原本的 μ μ μ 跟 σ \sigma σ。

那这个moving average应该要怎么计算呢?
其实也很简单,在training的时候,你每一次取一个 batch 出来的时候,你就会算一个 μ 1 μ^1 μ1,取第二个 batch 出来的时候,你就算个 μ 2 μ^2 μ2,一直到取第 t 个 batch 出来的时候,你就算一个 μ t μ^t μt,接下来把你已经算出来的这些 μ μ μ求一个平均值并乘上一个系数 p p p,这个 p p p也是一个超参数需要自己调整的,最后加上 ( 1 − p ) μ t (1-p)μ^t (1−p)μt ,来更新你的moving average μ ˉ \barμ μˉ,求 σ ˉ \bar\sigma σˉ 的过程也是类似的。
5 Batch Normalization 确实能帮助我们更好地训练神经网络
[1502.03167] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (arxiv.org)
下面的实验数据是从以上文献中截取的一张图片:
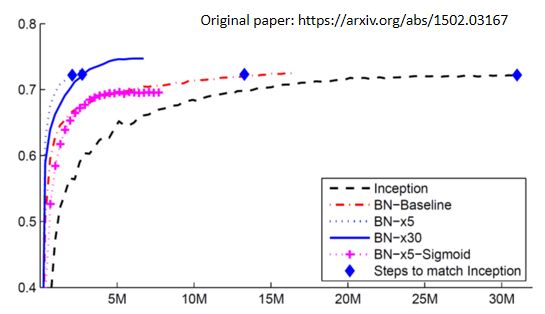
- 横轴代表的是训练的过程,纵轴代表的是训练出的模型在 validation set 上面的 accuracy
- 黑色的虚线是没有做 Batch Normalization 的结果,它用的是 inception 的 network,是一种以 CNN 为基础的 network 架构。
- 如果做了Batch Normalization,你会得到红色的这一条虚线(BN-Baseline),可以发现初期红色虚线训练的速度显然比黑色的虚线快很多,可以看到红色的虚线只用了不到一半的时间就达到了和黑色虚线一样的accuracy。
- 蓝色的实线(BN-x5)跟这个蓝色的虚线(BN-x30)呢,是把 learning rate 设大一点,x5和x30分别表示learning rate 是原来的 5 倍或30倍。因为如果做了 Batch Normalization 的话,error surface 会比较平滑,比较容易训练,所以就可以把你的 learning rate 设大一点,让训练的步子大一点,但learning rate设得太大也可能有问题,就比如这个图中30倍的 learning rate 最终训练出来的结果比5倍的 learning rate 效果要差一点。
- 最后是有一个加号表示的虚线(BN-x5-Sigmoid),作者这里想表达的是,就算是使用 sigmoid 生成了原本比较不好train的 error surface,加上 Batch Normalization 之后还是能够 train 的起来。作者也特意提到了如果 sigmoid 不加 Batch Normalization,根本连 train 都 train 不起来。
6 Batch Normalization 究竟为什么会有帮助呢?
在[1502.03167] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (arxiv.org)里面,作者他提出来一个概念,叫做 Internal Covariate Shift:
深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。为了训练好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。Google 将这一现象总结为 Internal Covariate Shift,简称 ICS。
Internal Covariate Shift与Normalization_lpty的博客-CSDN博客
作者认为我们在训练神经网络的时候会有下面这样的问题:
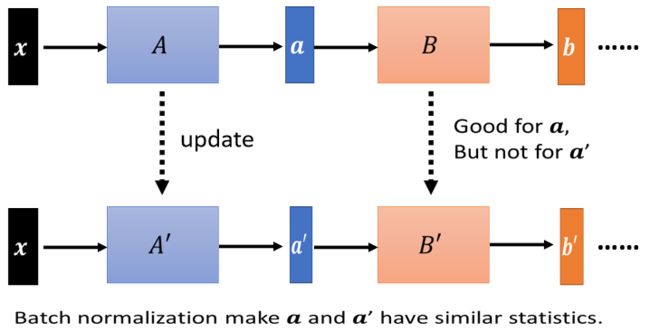
假如我们的network有很多层:
-
x 通过第一层以后得到 a
-
a 通过第二层以后得到 b
-
计算出 gradient 以后,把 A update 成 A′,把 B update 成 B′
作者在这里指出,我们在计算 B update 到 B′ 的 gradient 的时候,B 的输入是 a,接着把 A 更新为 A′ 之后,a 就变成了 a′,但是我们计算这个 B update 到 B′ 的 gradient 的时候,我们是根据 a 算出来的,所以这个 update 的方向或许适合用在 a 上,但不适合用在 a′ 上。
那如果我们每次都做了 batch normalization 的话,我们就会让 a 跟 a′ 的分布比较接近,这样也许就会对训练有帮助。

但是有一篇论文叫做 [1805.11604] How Does Batch Normalization Help Optimization? (arxiv.org),这篇文章的作者从多个角度来试图说明,internal covariate shift不一定是 training network 时候的一个问题,然后 Batch Normalization 有比较好的效果也不见得是因为它解决了 internal covariate shift 的问题。
那究竟为什么 Batch Normalization 会对训练有帮助呢,作者从实验上,也从理论上,支持了 Batch Normalization 可以改变 error surface,让 error surface 比较不崎岖的观点。
作者还发现,要让 error surface 变得比较不崎岖,也不一定只有 Batch Normalization 能做,作者也试了一些其他的方法,发现跟 Batch Normalization 的效果也差不多,甚至还稍微好一点。
总而言之呢,这篇论文的作者觉得,Batch Normalization 就像是盘尼西林一样,是一种偶然的发现,但无论如何,它仍然是一个在实践中被证明有效的方法,所以用就完事儿了。
附录:其他的标准化方法
Batch Normalization 并不是唯一的 normalization 的方法,以下是另外一些有名的方法:
Batch Renormalization
https://arxiv.org/abs/1702.03275
Layer Normalization
https://arxiv.org/abs/1607.06450
Instance Normalization
https://arxiv.org/abs/1607.08022
Group Normalization
https://arxiv.org/abs/1803.08494
Weight Normalization
https://arxiv.org/abs/1602.07868
Spectrum Normalization
https://arxiv.org/abs/1705.10941