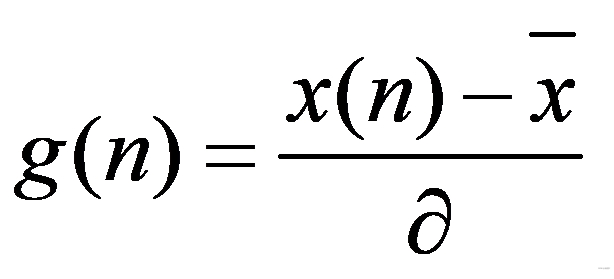Grubbs准则建模与分析 C与Matlab实现

个人网站 Geek交流圈
视频演示 B站视频

Grubbs准则建模与分析

目录

一、Grubbs准则定义及原理 1

1、 Grubbs定义 2
2、Grubbs原理 3
（1）具体流程： 3
（2）案例分析: 4

二、matlab程序设计及分析 7

1、matlab简介与使用方法 7
（1）开发环境 8
2、设计思路及相关函数 8
（1）定义测量值与显着度alpha 8
（2）画图函数 8
（3）计算 9
（4）确定g值 9
（5）比较异常值 10
（6）系统测试 11
3、完整源程序 13

三、C程序设计及分析 15

1、C开发环境及简介 15
（1）开发环境 15
2、设计思路及相关函数 15
（1）求平均值函数 15
（2）求标准差函数 16
（3）排序函数 16
（4）输出函数 16
（5）计算函数 17
（6）系统测试 18
3、完整源程序 19
四、实验总结 23

一、Grubbs准则定义及原理

1、Grubbs定义
格拉布斯准则，属于正态分布的分支，数学词汇。 格拉布斯准则是以正态分布为前提的，理论上较严谨，使用也方便。 某个测量值的残余误差的绝对值 |Vi |>Gg，则判断此值中有较大误差，应以剔除，此即格拉布斯准则。
格拉布斯准则是以正态分布为前提的，理论上较严谨，使用也方便。
某个测量值的残余误差的绝对值 |Vi |>Gg，则判断此值中有较大误差，应以剔除，此即格拉布斯准则。
利用格拉布斯(Grubbs)准则进行处理：
根据误差理论，要有效地剔除偶然误差，一般要测量10次以上，兼顾到精度和响应速度，取15次为一个单位。
在取得的15个数据中，有些可能含有较大的误差，需要对它们分检，剔除可疑值，提高自适应速度。对可疑值的剔除有多种准则，如莱以达准则、肖维勒（Chauvenet）准则、格拉布斯（Grubbs）准则等。
以Grubbs准则为例，它认为若某测量值 xi对应的残差Vi满足下式 |Vi|=| xi-x|>=g(n，a)× σ(X) 时应将该数据舍去。式中，x为n次采集到的AD 值的平均值，=(∑xi)/n ；σ(X)为测量数据组的标准差。
由贝塞尔函数可得： σ(X)=[(∑Vi2 )/(n-1)]1/2；g(n， a)是取决于测量次数n和显着性水平a (相当于犯“弃真” 错误的概率系数)，a通常取0.01或0.05。
通过查表可得：当 n=15时，a=0.05, g(n，a)=2.41。
把15次采集到的AD值存入一个数组中然后求平均值，计算残差，求标准差σ(X)。
将残差绝对值与2.41倍的标准差σ(X)比较。剔除可疑值以后，再求平均值，求出新的平均值以后，应再重复以上过程，验证是否还有可疑值存在。据我们对测量装置大量的实际测试结果看，这样做没有什么必要，因为一般只有第一遍即可达到要求。
然而这种方法也有它的不足, 利用Grubbs准则需要处理大量的数据，而在一般的工业现场测试设备中，仪表结构大多采用嵌入式结构，如AVR单片机。这些MCU程序空间和数据空间有限，若处理大量数据，难以满足资源要求。而且，由于Grubbs准则要求MCU进行大量数据处理，使得系统降低了信号采集速率，影响实时性。
什么数据可能含有粗大误差？ 在一段序列中，过高或过低的数，如下图。

图1-1 粗大误差分析图
2、Grubbs原理
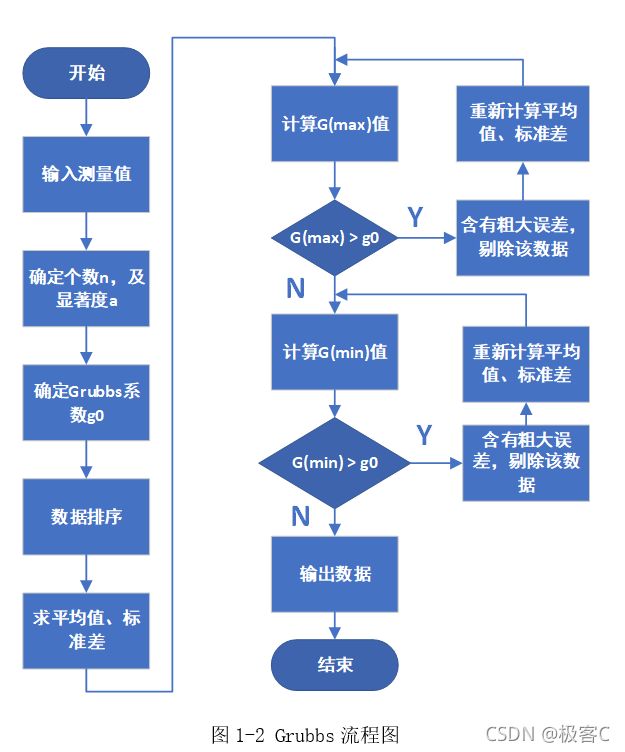
（1）具体流程：
1、定义输入数据 data[n]
确定数据个数 n
2、选取显着度 a 一般是0.01或者0.05

3、通过查阅格拉布斯系数表，可以确定格拉布斯系数 ，由n和a确定。
4、将数据进行排序，由小到大，由大到小都可以。
5、求数学期望，也就是平均值
6、求标准差

若认为x(n)可疑，则有

如果 ，则该测量值含有粗大误差，应该剔除。
具体怎么判断呢？
因为含有粗大误差的数是过高或过低的数，那么我们就需要判断最大值与最小值。假如最大值含有粗大误差，那么需要剔除最大值，然后重新计算平均值与标准差，再求出 ，继续判断，直到最大值没有含粗大误差为止。需注意最大值剔除后，原来的第二大值就成为的最大值，所以我们一直是判断最大值。
（2）案例分析
1、定义n个数据 1,2 ,3 ,4 ,9, 8, 7, 6, 17 ,5,10
这里n = 11；
2、设置显着度a = 0.01；（自己设定，一般为0.01或0.05）
需注意，在不同的a下，同一数据可能得到的结果不同，案例分析。
通过查表可知：
当n = 11，a = 0.01时， = 2.48；
当n = 11，a = 0.05时， = 2.23；
3、从小到大排序为： 1 2 3 4 5 6 7 8 9 10 17
平均值 为：6.546
标准差 为：4.293

4、计算g(max) 与g(min) ，计算公式如下

判断最小值： =1.292 < = 2.48 不含粗大误差
判断最大值： =2.435 < = 2.48 不含粗大误差
说明在显着度a = 0.01时，上面的数据没有含有粗大误差。

当我们取g = 0.05时， = 2.23
平均值 为：6.546
标准差 为：4.293
判断最小值： =1.292 < = 2.23 不含粗大误差
判断最大值： =2.435 > = 2.23 含有粗大误差
所以将最大值剔除，也就是将17剔除，那么最大值变为10
重新求平均值与标准差
平均值 为：5.50
标准差 为：2.87
再求此时的 与
判断最小值： =1.567 < = 2.23 不含粗大误差
判断最大值： =1.567 < = 2.23 不含粗大误差
判断结束，消除粗大误差的数据为
1 2 3 4 9 8 7 6 5 10 （未排序）
1 2 3 4 5 6 7 8 9 10 （排序后）

由上例分析，同样的数据，当显着度a=0.01时，数据未含有粗大误差；当显着度a=0.05时，数据含有粗大误差。这说明数据是否含有粗大误差是相对的，与自己的初始条件有关。
不同的分析方法得到的结果可能不同。
下面是Grubbs准则的流程图，需要了解逻辑，在程序设计的过程中，就是根据该逻辑进行设计。

图1-2 Grubbs流程图

图1-3 格拉布斯系数表

二、matlab程序设计及分析

1、matlab简介与使用方法
（1）开发环境
MATLAB是美国MathWorks公司出品的商业数学软件，用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人，控制系统等领域。
MATLAB是matrix&laboratory两个词的组合，意为矩阵工厂（矩阵实验室），软件主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言（如C、Fortran）的编辑模式。
本例程使用MATLAB R2016a进行实验。
2、设计思路及相关函数
（1）定义测量值与显着度alpha

%定义序列  
2.	a=[ 1,2 ,3 ,4 ,9, 8, 7, 6, 17 ,5,10];   
3.	%输入显着度alpha  
4.	alpha=input('(请输入alpha的值0.01或0.05)');  
程序说明：
a 就是一维数组，数据个数为11，alpha为显着度，让我们自己输入，一般为0.01或0.05。

（2）画图函数

1.	subplot(121);stem(a,'filled'); %subplot函数是在平铺位置创建坐标区  
2.	xlabel('序列个数n'); %xlabel函数 为 x 轴添加标签  
3.	ylabel('幅值'); %ylabel函数 为 y 轴添加标签  
4.	title('原序列'); %添加标题  
5.	%axis([0 25 0 30]);  
6.	axis([0 15 -20 20]); %设置坐标轴范围和纵横比 

程序说明：
subplot(mnp)参数说明
m表示是图排成m行
n表示图排成n列
p是指你现在要把曲线画到figure中哪个图上，最后一个如果是1表示是从左到右第一个位置
stem函数是绘制离散序列数据，以实心的方式画出茎秆。
如图2-1所示，对比程序中的文字说明，查看各函数的对应关系。

图2-1 画图程序显示
（3）计算

1.	n=length(a); %得到序列a的长度  
2.	avg=mean(a); %求数组的均值  
3.	st=std(a,1); %求标准差  
4.	a_max = max(a); % a数组中的最大值  
5.	a_min = min(a); % a数组中的最小值  
6.	reg_max=abs((max(a)-avg)/st); %求最大值的Grubbs系数  
7.	reg_min=abs((min(a)-avg)/st); %求最小值的Grubbs系数 

程序说明：
在matlab中，很多数学公式都已经封装成为了函数，只需要了解函数的运用就行，具体函数内容看程序中的注释，每一步都有说明。
（4）确定 g 值

1.	%确定g值  
2.	T_01=[0 0 1.155 1.492 1.749 1.944 2.097 2.22 2.323 2.41 2.485 2.55 2.607];  
3.	T_05=[0 0 1.153 1.463 1.672 1.822 1.938 2.032 2.11 2.176 2.234 2.285 2.331];
4.	switch (alpha) %由显着度 alpha 确定T的取值，  
5.	case 0.05   
6.	g=T_05(n);  
7.	case 0.01   
8.	g=T_01(n);  
9.	otherwise %disp('输入了错误的alpha值');   
程序说明：
    在我们输入显着度a过后，在这段程序运行就能得到 。

（5）比较异常值

	%比较异常值  
2.	if reg_max>g %判断最大值  
3.	    flag_2=1;  
4.	    abn=max(a);  
5.	    disp('被剔除的数据为')  
6.	    disp(abn);  
7.	    a(a==max(a))=[];  
8.	else if reg_min>g %判断最小值  
9.	     flag_2=1;  
10.	    abn=min(a);  
11.	    disp('被剔除的数据为')  
12.	    disp(abn);  
13.	    a(a==min(a))=[];  
14.	    else  %没有含有粗大误差的数啦  
15.	    flag_1=0; %标志清为0，退出while循环  
16.	    %画出处理好的序列图像  
17.	    subplot(122);stem(a,'filled');  
18.	    title('处理后的序列');  
19.	    xlabel('序列个数n');  
20.	    ylabel('幅值');  
21.	    axis([0 15 -20 20]);  
22.	    end  
23.	end  

程序说明：
先判断最大值是否含有粗大误差，再判断最小值是否含有粗大误差，当都没有粗大误差的时候，输出数据。
（6）系统测试
图2-2 matlab操作页面

图2-3 程序运行指令

图2-4 a = 0.05数据显示图

图2-5 a = 0.02数据显示图
由程序运行可知，我们需要输入显着度alpha，0.01或者0.05。当我们输入0.05时，经程序分析，数据17与-15含有粗大误差，剔除数据17与-15过后，再进行计算，当没有粗大误差时，最后显示出处理后的序列。
3、完整源程序

1.	%定义序列  
2.	a=[ -15,2 ,3 ,4 ,9, 8, 7, 6, 17 ,5,10];   
3.	  
4.	%输入显着度alpha  
5.	alpha=input('(请输入alpha的值0.01或0.05)');  
6.	  
7.	%关于画图程序==========================================================================  
8.	subplot(121);stem(a,'filled'); %subplot函数是在平铺位置创建坐标区   stem函数是绘制离散序列数据，以实心的方式画出茎秆。  
9.	%subplot(mnp)参数说明  
10.	%m表示是图排成m行，n表示图排成n列   
11.	%p是指你现在要把曲线画到figure中哪个图上，最后一个如果是1表示是从左到右第一个位置  
12.	  
13.	xlabel('序列个数n'); %xlabel函数 为 x 轴添加标签  
14.	ylabel('幅值'); %ylabel函数 为 y 轴添加标签  
15.	title('原序列'); %添加标题  
16.	%axis([0 25 0 30]);  
17.	axis([0 15 -20 20]); %设置坐标轴范围和纵横比  
18.	  
19.	flag_1=1; %设置标志变量  
20.	flag_2=0;  
21.	  
22.	%计算  
23.	while flag_1==1  %while开始  
24.	n=length(a); %得到序列a的长度  
25.	avg=mean(a); %求数组的均值  
26.	st=std(a,1); %求标准差  
27.	a_max = max(a); % a数组中的最大值  
28.	a_min = min(a); % a数组中的最小值  
29.	reg_max=abs((max(a)-avg)/st); %求最大值的Grubbs系数  
30.	reg_min=abs((min(a)-avg)/st); %求最小值的Grubbs系数  
31.	  
32.	%确定g值  
33.	T_01=[0 0 1.155 1.492 1.749 1.944 2.097 2.22 2.323 2.41 2.485 2.55 2.607];  
34.	T_05=[0 0 1.153 1.463 1.672 1.822 1.938 2.032 2.11 2.176 2.234 2.285 2.331];  
35.	switch (alpha) %由显着度 alpha 确定T的取值，  
36.	case 0.05   
37.	g=T_05(n);  
38.	case 0.01   
39.	g=T_01(n);  
40.	otherwise %disp('输入了错误的alpha值');   
41.	end  %while循环结束  
42.	  
43.	%比较异常值  
44.	if reg_max>g %判断最大值  
45.	    flag_2=1;  
46.	    abn=max(a);  
47.	    disp('被剔除的数据为')  
48.	    disp(abn);  
49.	    a(a==max(a))=[];  
50.	else if reg_min>g %判断最小值  
51.	     flag_2=1;  
52.	    abn=min(a);  
53.	    disp('被剔除的数据为')  
54.	    disp(abn);  
55.	    a(a==min(a))=[];  
56.	    else  %没有含有粗大误差的数啦  
57.	    flag_1=0; %标志清为0，退出while循环  
58.	    %画出处理好的序列  
59.	    subplot(122);stem(a,'filled');  
60.	    title('处理后的序列');  
61.	    xlabel('序列个数n');  
62.	    ylabel('幅值');  
63.	    axis([0 15 -20 20]);  
64.	    end  
65.	end  
66.	  
67.	if flag_2==0   
68.	disp('没有异常数据');  
69.	end;  
70.	  
71.	end;  

三、C程序设计及分析

1、C开发环境及简介
Microsoft Visual Studio（简称VS）是美国微软公司的开发工具包系列产品。VS是一个基本完整的开发工具集，它包括了整个软件生命周期中所需要的大部分工具，如UML工具、代码管控工具、集成开发环境(IDE)等等。所写的目标代码适用于微软支持的所有平台，包括Microsoft Windows、Windows Mobile、Windows CE、.NET Framework、.NET Compact Framework和Microsoft Silverlight 及Windows Phone。
本例程使用Visual Studio 2019进行实验。
2、设计思路及相关函数
因为标准C中并没有那么丰富的数学函数，很多需要自己造，所以在本次实验过程中平均值，标准差，排序这些都是自己写的函数。虽然自己写繁琐了一点，但个人觉得能更好的掌握原理，对自己有很大帮助。

（1）求平均值函数

1.	//求数学期望  
2.	float MathExp(float* data, int start, int end)  
3.	{
       
4.	    float ex = 0;  
5.	    int count = 0;  
6.	    for (int i = start; i <= end; i++)  
7.	    {
       
8.	        ex += data[i];  
9.	        count++;  
10.	    }  
11.	    ex /= count;  
12.	    return ex;  
13.	}  

（2）求标准差函数

1.	//求标准差  
2.	float StdDev(float* data, int start, int end)  
3.	{
       
4.	    float ex = MathExp(data, start, end);  
5.	    float sd = 0;  
6.	    int count = 0;  
7.	    for (int i = start; i <= end; i++)  
8.	    {
       
9.	        sd += pow(data[i] - ex, 2);  
10.	        count++;  
11.	    }  
12.	    sd = sqrt(sd / count);  
13.	    return sd;  
14.	}

（3）排序函数

1.	//排序  
2.	void Sort(float* data, int n)  
3.	{
       
4.	    for (int i = 1; i < n; i++)  
5.	    {
       
6.	        for (int j = 0; j < n - i; j++)  
7.	        {
       
8.	            if (data[j] > data[j + 1])  
9.	            {
       
10.	                float temp = data[j];  
11.	                data[j] = data[j + 1];  
12.	                data[j + 1] = temp;  
13.	            }  
14.	        }  
15.	    }  
16.	} 

（4）输出函数

1.	//输出数组  
2.	void Print(float* data, int n)  
3.	{
       
4.	    for (int i = 0; i < n; i++)  
5.	    {
       
6.	        printf("%0.3lf ", data[i]);  
7.	    }     
8.	    printf("\n");  
9.	}

（5）计算函数

1.	float ex = MathExp(data, start, end); //求数学期望  
2.	float sd = StdDev(data, start, end); //求标准差  
3.	  
4.	printf("数学期望为：%0.3lf\n 标准差为：%0.3lf\nT: %0.3lf\n", ex, sd, T[n - 1]);  
5.	float g0_min = (fabs(data[start] - ex)) / sd;  
6.	if ((fabs(data[start] - ex)) / sd >= T[n - 1]) //fabs是求绝对值  
7.	{
       
8.	    printf("%lf 为粗大误差，应剔除\n", data[start]);  
9.	    n--;  
10.	    start++;  
11.	    flag = 1;  
12.	}  
13.	  
14.	float g0_max = (fabs(data[end] - ex)) / sd;  
15.	if ((fabs(data[end] - ex)) / sd >= T[n-1])  
16.	{
       
17.	    printf("%0.3lf 为粗大误差，应剔除\n", data[end]);  
18.	    n--;  
19.	    end--;  
20.	    flag = 1;  
21.	}  
22.	if (!flag)  
23.	{
       
24.	    printf("余下数据无坏值\n余下数据为：\n");  
25.	    Print_Part(data, start, end);  
26.	    printf("\n");  
27.	} 

（6）系统测试

图3-1 VS2019操作页面

图3-2 a = 0.05运行显示

图3-1 a = 0.01运行显示
3、完整源程序

1.	#define _CRT_SECURE_NO_WARNINGS  
2.	#include <stdio.h>  
3.	#include <stdlib.h>  
4.	#include <string.h>  
5.	#include <math.h>  
6.	  
7.	//求数学期望  
8.	float MathExp(float* data, int start, int end)  
9.	{
       
10.	    float ex = 0;  
11.	    int count = 0;  
12.	    for (int i = start; i <= end; i++)  
13.	    {
       
14.	        ex += data[i];  
15.	        count++;  
16.	    }  
17.	    ex /= count;  
18.	    return ex;  
19.	}  
20.	  
21.	//求标准差  
22.	float StdDev(float* data, int start, int end)  
23.	{
       
24.	    float ex = MathExp(data, start, end);  
25.	    float sd = 0;  
26.	    int count = 0;  
27.	    for (int i = start; i <= end; i++)  
28.	    {
       
29.	        sd += pow(data[i] - ex, 2);  
30.	        count++;  
31.	    }  
32.	    sd = sqrt(sd / count);  
33.	    return sd;  
34.	}  
35.	  
36.	  
37.	//排序  
38.	void Sort(float* data, int n)  
39.	{
       
40.	    for (int i = 1; i < n; i++)  
41.	    {
       
42.	        for (int j = 0; j < n - i; j++)  
43.	        {
       
44.	            if (data[j] > data[j + 1])  
45.	            {
       
46.	                float temp = data[j];  
47.	                data[j] = data[j + 1];  
48.	                data[j + 1] = temp;  
49.	            }  
50.	        }  
51.	    }  
52.	}  
53.	  
54.	//输出数组  
55.	void Print(float* data, int n)  
56.	{
       
57.	    for (int i = 0; i < n; i++)  
58.	    {
       
59.	        printf("%0.3lf ", data[i]);  
60.	    }     
61.	    printf("\n");  
62.	}  
63.	  
64.	//输出部分数组  
65.	void Print_Part(float* data, int start, int end)  
66.	{
       
67.	    for (int i = start; i <= end; i++)  
68.	    {
       
69.	        printf("%0.3lf ", data[i]);  
70.	    }  
71.	    printf("\n");  
72.	  
73.	}  
74.	  
75.	int main()  
76.	{
       
77.	    /* 
78.	        本次测试的数据个数为11  显着度设为0.01   
79.	        如果要测试其他数据，直接修改即可 
80.	        26.773, 50, 26.774, 26.778, 26.771, 26.780, 26.772, 26.777, 26.775, 26.774, 26.774 
81.	    */  
82.	    float data[11] = {
      1,2 ,3 ,4 ,9, 8, 7, 6, 17 ,5,10 };  
83.	    float T_05[11] = {
      0, 0, 1.15, 1.46, 1.67, 1.82, 1.94, 2.03, 2.11, 2.18, 2.23 };  
84.	    float T_01[11] = {
      0, 0, 1.15, 1.49, 1.75, 1.94, 2.10, 2.22, 2.32, 2.41, 2.48 };  
85.	    float T[11] = {
      0 };  
86.	    char a_flag[5] = {
      0 };  
87.	  
88.	    printf("请输入显着度a（0.01或0.05）：");  
89.	    scanf("%s", &a_flag);  
90.	    if (!strcmp(a_flag,"0.05")) //相同返回0  
91.	    {
       
92.	        for (int i = 0; i < 11; i++)  
93.	        {
       
94.	            T[i] = T_05[i];  
95.	        }  
96.	    }  
97.	    else if (!strcmp(a_flag, "0.01")) //相同返回0  
98.	    {
       
99.	        for (int i = 0; i < 11; i++)  
100.	        {
       
101.	            T[i] = T_01[i];  
102.	        }  
103.	    }  
104.	    else  
105.	    {
       
106.	        printf("输入参数错误，默认为a = 0.05\n");  
107.	        for (int i = 0; i < 11; i++)  
108.	        {
       
109.	            T[i] = T_05[i];  
110.	        }  
111.	    }  
112.	  
113.	    int n = 11;  
114.	    printf("本次处理的测量数据为: \n");  
115.	    Print(data, n);  
116.	    printf("\n");  
117.	  
118.	    printf("从小到大排序: \n");  
119.	    Sort(data, n);  
120.	    Print(data, n);  
121.	    printf("\n");  
122.	  
123.	    int start = 0;  
124.	    int end = n - 1;  
125.	    char flag = 1;  
126.	    while (flag)  
127.	    {
       
128.	        flag = 0;  
129.	        float ex = MathExp(data, start, end); //求数学期望  
130.	        float sd = StdDev(data, start, end); //求标准差  
131.	  
132.	        printf("数学期望为：%0.3lf\n 标准差为：%0.3lf\nT: %0.3lf\n", ex, sd, T[n - 1]);  
133.	        float g0_min = (fabs(data[start] - ex)) / sd;  
134.	        if ((fabs(data[start] - ex)) / sd >= T[n - 1]) //fabs是求绝对值  
135.	        {
       
136.	            printf("%lf 为粗大误差，应剔除\n", data[start]);  
137.	            n--;  
138.	            start++;  
139.	            flag = 1;  
140.	        }  
141.	  
142.	        float g0_max = (fabs(data[end] - ex)) / sd;  
143.	        if ((fabs(data[end] - ex)) / sd >= T[n-1])  
144.	        {
       
145.	            printf("%0.3lf 为粗大误差，应剔除\n", data[end]);  
146.	            n--;  
147.	            end--;  
148.	            flag = 1;  
149.	        }  
150.	        if (!flag)  
151.	        {
       
152.	            printf("余下数据无坏值\n余下数据为：\n");  
153.	            Print_Part(data, start, end);  
154.	            printf("\n");  
155.	        }  
156.	    }  
157.	    return 0;  
158.	}  

四、实验总结

• 通过建模分析，不仅让我对Grubbs准则有了更深刻的认识，而且对matlab、C编程更加熟练。其实Grubbs原理并不是很难，但是建模与实际应用加大了难度，在编写这篇论文的时候，反复去查阅资料与实际测试，因为要保证程序的健全性以及数据的准确性，总不能得到错误的运行结果吧。在这里我不得不吐槽一下，网上的一些资料真是误人子弟，很多都是错误的，模棱两可的也很多。

• 在实际编程过程中，用C的时间比较多，因为要自己写些函数。后来想用C++实现一下的，因为有STL比较方便，后来觉得没啥意思，觉得C和matlab是两个最好的代表了，一个偏底层，一个偏应用。

• 最开始是想随便实现下的，但是觉得既然做了，那就要做到最好，所以写论文，刨析原理，不同的方法去建模分析，不仅要让自己懂，也要让别人懂。喜欢将复杂的知识用最简易的话描述出来，而不是一堆学术用词，让不懂的人在里面反复打滚。

• 平时都对课程没啥兴趣，一般都是做几个题，写在本子上，念念理论，实在无聊，又没啥进步。相反我更喜欢自由发挥的，做项目，写论文，从写方案，到设计与实现，每一步都能让自己收获巨大，这些都是课本上学不到的。