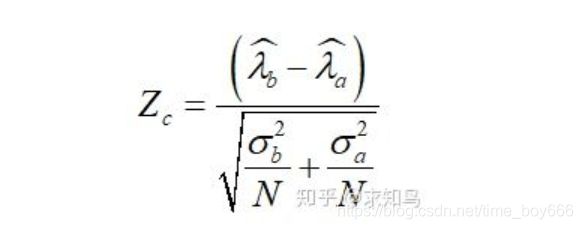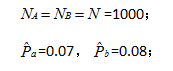关于 ABtest 实验在数据分析中的一些事~
参考文章:
https://blog.csdn.net/zzq900503/article/details/70991497?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
https://zhuanlan.zhihu.com/p/75762862
在网站和移动产品设计和开发中、以及互联网产品运营中,我们经常会面临多个产品设计和运营方案的选择,比如某个按钮是用红色还是用蓝色,是放左边还是放右边。传统的解决方法通常是集体讨论表决,或者由某位专家或领导来拍板,实在决定不了时也有随机选一个上线的。虽然传统解决办法多数情况下也是有效的,但A/B 测试(A/B Testing)可能是解决这类问题的一个更好的方法。
在软件开发中,产品需求通过多种技术手段来实现; A/B测试实验提供了一个有价值的方式来评估新功能对客户行为的影响。
在运营过程中,AB测试用得更加普遍,比如发送邮件或者广告,先拿小样本,测试多个版本,数据表明哪一个广告或邮件的转化率高,就用哪一个邮件或广告。
1 什么是A/B测试?
A/B测试是一种流行的网页优化方法,可以用于增加转化率注册率等网页指标。简单来说,就是为同一个目标制定两个方案(比如两个页面),将产品的用户流量分割成 A/B 两组,一组试验组,一组对照组,两组用户特点类似,并且同时运行。试验运行一段时间后分别统计两组用户的表现,再将数据结果进行对比,就可以科学的帮助决策。比如在这个例子里,50%用户看到 A 版本页面,50%用户看到 B 版本页面,结果 A 版本用户转化率 23%,高于 B 版本的 11%,在试验流量足够大的情况下,我们就可以判定 A 版本胜出,然后将 A 版本页面推送给所有的用户。
AB测试本质上是个分离式组间实验,以前进行AB测试的技术成本和资源成本相对较高,但现在一系列专业的可视化实验工具的出现,AB测试已越来越成为网站优化常用的方法。
A/B测试其实是一种“先验”的实验体系,属于预测型结论,与“后验”的归纳性结论差别巨大。A/B测试的目的在于通过科学的实验设计、采样样本代表性、流量分割与小流量测试等方式来获得具有代表性的实验结论,并确信该结论在推广到全部流量可信。
2 什么情况不适合做 A/B 测试?
有时多个设计稿可能会有非常大的差异,这样的情况一般不太适合做 A/B 测试,因为它们的变量太多了,变量之间会有较多的干扰,很难通过 A/B 测试的方法来找出各个变量对结果的影响程度。(在实际的实验设计中,要尽可能把一些其他的干扰因素排除,基本的思想就是物理实验里面的控制变量法)
另外,虽然 A/B 测试名字中只包含 A、B ,但并不是说它只能用于比较两个方案的好坏,事实上,你完全可以设计多个方案进行测试,“A/B 测试”这个名字只是一个习惯的叫法。回到网站设计,一般来说,每个设计方案应该大体上是相同的,只是某一个地方有所不同,比如某处排版、文案、图片、颜色等。然后对不同的用户展示不同的方案。
要注意,不同的用户在他的一次浏览过程中,看到的应该一直是同一个方案。比如他一开始看到的是 A 方案,则在此次会话中应该一直向他展示 A 方案,而不能一会儿让他看 A 方案,一会儿让他看 B 方案。同时,还需要注意控制访问各个版本的人数,大多数情况下我们会希望将访问者平均分配到各个不同的版本上。要做到这些很简单,根据 cookie (比如 cookie 会话ID的最后一位数字)决定展示哪个版本就是一个不错的方法。
3 一些例子帮助理解
AB 测试是撬动理性增长的最重要工具之一。AB测试背后的理念是在于用数据来帮助你做决策,来帮助你做更好的决策,很多东西就不再是靠艺术创造、靠想象、靠拍脑袋来做,而是靠数据,像你写代码、做分析的时候那样一种很理性的模式。
如果没有 AB 测试,如果公司盲目地前行,会造成很大的损失。
- 在 Facebook 强行规定,发布任何一个很大功能的时候,开始要先计划,同时要做一个预期,计划就是你这个功能发布之后,大概周期是多久,你的预期就是对用户的数据大概有怎样的影响,一般来说是用户的活跃度上涨,或者是用户的数量上涨,但是可能有其他的影响。比如说用户的在线时长会下降一点点,因为你更加有效了,或者是对用户的耗电量会有影响,以及它流量的损耗。
-
携程机票的ABTest实践。
4 关于设计实验的一些理论知识
参考知乎的一篇回答:https://zhuanlan.zhihu.com/p/75762862
概率论之二项分布的应用(这个概念讲解特别nice)
A/B-test是为同一个目标制定两个方案,在同一时间维度,分别让组成成分相同(相似)的用户群组随机的使用一个方案,收集各群组的用户体验数据和业务数据,最后根据显著性检验分析评估出最好版本正式采用。
A/B-test显著性检验
随机将测试用户群分为2部分,用户群1使用A方案,用户群2使用B方案,经过一定测试时间后,根据收集到的两方案样本观测数据,根据显著性检验结果选取最好方案。
为了下文方便说明,我们不妨设A方案为参考方案(或旧方案),B方案为实验方案(或新方案)。
由于每次实验结果要么转化成功,要么失败,所以A,B的分布可看作是伯努利分布;
我们知道,二项分布当n-->无限时,可以近似的看作服从正态分布;其 均值 和 方差 为:
并且在抽样时,A/B组的用户的各种属性要相似。比如(近10天登陆频次,用户近10天消费情况,用户静态属性)
假设检验:
参考:https://www.cnblogs.com/hdu-zsk/p/6293721.html
(显著性检验是用于检测科学实验中 实验组 与 对照组 之间是否有差异 以及差异是否显著的办法)
按照假设检验的“套路”,H1是我们想要的假设,H0是要拒绝的假设:
由于是双样本均值显著性检测,我们可以用Z检验:
网上提供的AB测试样本量计算器:
l Statistical power(1-β)
l Significance Level (α)Statistical Significance(1-α)
l Baseline rate(conversation rate)
l Minimum detectable effect
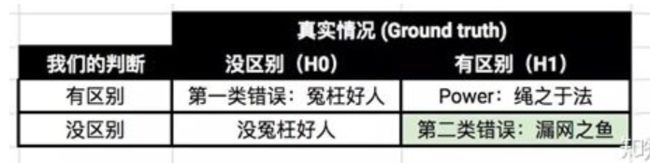
由于判断错了,我们把这类错误叫做第一类错误(Type I error),我们把第一类错误出现的概率用α表示。这个α,就是Significance Level。一般选择5%,即保证第一类错误的概率不超过5%。Statistical Significance=1-level,表示有多大的把握不冤枉好人!
判断正确。我们把做出这类正确判断的概率叫做Statistical Power。这一个一般要大!
我们的判断又错了。这类错误叫做第二类错误(Type II error),用β表示。根据条件概率的定义,可以计算出β = 1 - power。
总结一下,对于我们的实验:
- · 第一类错误α不超过5%。也就是说Statistical Significance =1-α=95%
- · 第二类错误β不超过20%。也就是说,Statistical Power = 1 -β = 80%。
对α与β的理解:
对两类错误上限的选取(α是5%,β是20%),我们可以了解到A/B实验的重要理念:宁肯砍掉4个好的产品,也不应该让1个不好的产品上线。
baseline Rate:
这个看的是在实验开始之前,对照组本身的表现情况。在我们的实验里,baseline就是旧方案的点击率;
- 这个参数越小,你需要的样本量越大(分母越大,这个参数越小)
- 这个参数越大,你需要的样本量越小
在工作中,这个参数完全是历史数据决定的。在我们的实验中,我们假定,实验开始之前的历史点击率是5%。所以Baseline Rate=5%。
Minimum Detectable Effect
顾名思义,这个参数衡量了我们对实验的判断精确度的最低要求。
- 参数越大(比如10%),说明我们期望实验能够检测出10%的差别即可。检测这么大的差别当然比较容易(power变大),所以保持power不变的情况下,所需要的样本量会变小。
- 参数越小(比如1%),说明我们希望实验可以有能力检测出1%的细微差别。检测细微的差别当然更加困难(power变小)所以样本量越大,所以如果要保持power不变的话,需要的样本量会增加。
在工作中,这个参数的选定往往需要和业务方一起拍板。在我们的实验中,我们选定Minimum Detectable Effect=5%。这意味着,如果“签到赚钱”真的提高了点击率5个百分点以上,我们希望实验能够有足够把握检测出这个差别。如果低于5个百分点,我们会觉得这个差别对产品的改进意义不大(可能是因为点击率不是核心指标),能不能检测出来也就无所谓了。
==========================================================================================
个人理解:
| 方案决策 | 真实情况(H0对) | 真实情况(H0错误) |
| A方案好(H0) | 接受A方案(正确) | 错误的接受A方案 (弃真错误) |
| B方案好(拒绝H0) | 错误的接受B方案 (取伪错误) |
接受B方案(正确) |
5 结合上面的理论加入实际讨论01
假设检验还可以这样做(如果假设都能满足的话)
某公司想知道产品优化是否有效,设立实验组与对照组收集一周点击率,请检验产品优化是否有效
ABtest和假设检验、流量分配
- A方案(实验组)7天点击率分别为:0.72,0.75,0.7,0.75,0.73,0.72,0.71
- B方案(对照组)7天点击率分别为:0.7,0.76,0.69,0.75,0.7,0.69,0.68
由于不同统计日之间是有随机波动的差异,而且实验组和对照组流量相等且随机,可以认为样本来自同一个总体,实验组是对同一天的对照组进行优化的结果,所以可以采用相关样本t检验。
Step1:
- H0:功能优化之后与优化前没有差异(μ2-μ1=0)
- H1:功能优化之后与优化前有差异(μ2-μ1≠0)
- μ为点击率
Step2:确定显著性水平α=0.05
Step3:计算统计量,相关样本t检验是以每一组数据的差值作为检验的,所以以点击率差作检验
- day1:0.72-0.7=0.02
- day2:0.75-0.76= -0.01
- day3:0.7-0.69=0.01
- day4:0.75-0.75=0
- day5:0.73-0.7=0.03
- day6:0.72-0.69=0.03
- day7:0.71-0.68=0.03
Md为七组差值的均值,经计算为0.0157;
计算差值的方差:(0.02-0.016)^2+……+(0.03- 0.016)^2/(7-1)=0.000262,开根号得到标准误=0.0161,最后代入t分数:t=0.0157-0/0.0161=0.97
Step4:查表,按α=0.05,df=n-1,确定临界值,2.447。 T检验临界值表 (样本小,用T分布T检验)
Step3中的t=0.97在临界值内,接受零假设,认为功能优化没有效果。
6 结合上面的理论加入实际讨论02
参考:https://blog.csdn.net/buracag_mc/article/details/74905483
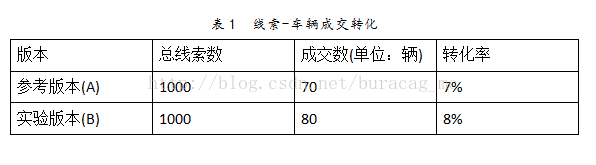
假设我们进行A/B-test一周,参考版本(通常默认是原始版本,简记为A)和实验版本(添加了特定改进的版本,简记为B),分别得到了1000个线索,A的线索-车辆成交转化率为7%,B的线索-车辆成交转化率为8%。如表1所示:
计算步骤:
2.构建原假设和备择假设:
3.构建检验统计量:
我们可以计算得到 Z=0.849105726
4.显著性检验结论:
样本数量大于30用Z分布,但是由于样本数量大于30的时候,Z分布和T分布接近,也可以用T方便计算
如果取显著性水平=0.5,则=1.644854,所以不能拒绝原假设,即认为B版本不一定比A版本所带来的线索-车辆成交转化率高。
如果我们将A/B-test的时间拉长,如两周时长的A/B-test分别得到5000条线索量;或者说同样做一周时间的A/B-test,但是测试的比例更大,分别得到5000条线 索量。即 N=5000,且线索-车辆成交转化率保持不变。计算得出Z=1.89865812,在同样显著性水 平下,可以拒绝原假设,得出B比A版本所带来的线索-车辆成交转化率高的结论。
上述结论是符合我们的主观感受的!在小样本量时,新版所带来的线索-车辆成交转化率高于旧版本所带来的线索-车辆成交转化率,其原因也有可能是受到随机波动等因素影响,故不能肯定地说明新版要比旧版所带来的线索-车辆成交转化率高;但在大样本量时,或者说长期来看,新版本所带来的线索-车辆成交转化率都稳定地高于旧版本所带来的线索-车辆成交转化率,我们有理由相信,确实新版本所带来的线索-车辆成交转化率高于旧版本所带来的线索-车辆成交转化率。