机器学习（7）BP神经网络

概述

BP(Back Propagation)神经网络，即反向传播神经网络。它是一种按误差逆向传播算法训练的多层前馈网络，并且层与层之间存储着大量输入-输出映射关系。它的训练规则是通过把误差反向传播，使用梯度下降算法，从而调整网络中的权重，是的最终误差最小。

基本思想

它有三层组成：输入层、隐含层和输出层。隐含层的权重我们无法得知，但是可以通过输出层结果和预期结果的误差来间接调整隐含层的权重。

1. 正向传播：输入样本通过输入层输入，由中间的隐含层进行处理后，由输出层输出。若输出的结果与预期的结果有差距，则转向反向传播阶段。
2. 反向传播：将误差通过输出层反向传播，期间将误差分摊给各个单元，各个单元通过该误差调整权重。

激活函数

激活函数是神经网络中神经元（一般是隐含层）节点上运行的函数，它负责把神经元的输入映射到输出，这里的映射是指非线性映射。如果不使用激活函数，那么每一层的输入输出都是线性运算，无法解决具体问题。使用了激活函数，就可以使整个神经网络逼近任何一个非线性函数。
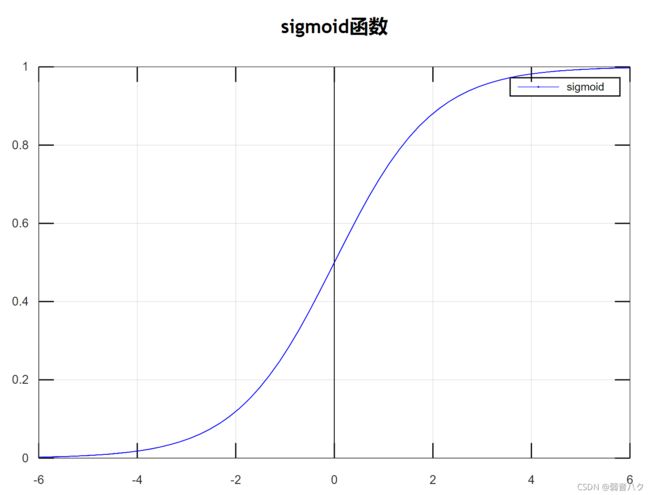
目前有多种激活函数，本文所使用的激活函数：sigmoid函数，它能将变量映射到0~1之间。
$$f(x)=\frac{1}{1+e^{(-x)}}$$
图像如下：

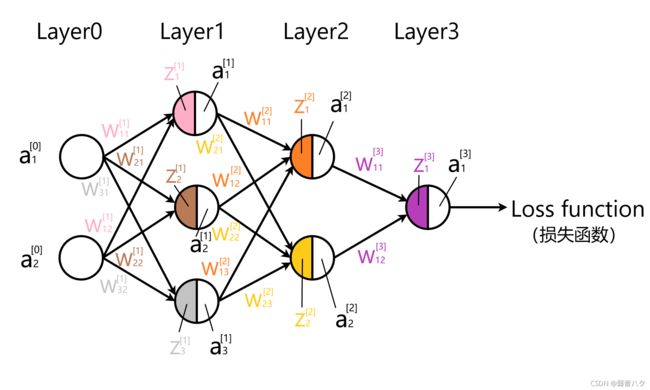
BP神经网络结构

第0层是输入层，第1层是第一层隐含层，第2层是第二层隐含层，第三层是输出层(对于多分类问题，输出层的神经元不只一个）

符号约定

$w_{jk}^{[l]}$ 表示从网络中第$（l-1)$层第$k$个神经元到第$l$层第$j$个神经元的连接权重，同时也是第 $l$ 层权重矩阵第 $j$ 行第 $k$ 列的元素。
$b_j^{[l]}$ 表示第$l$层第$j$ 个神经元的偏置，同时也是第$l$ 层偏执向量的第$j$个元素。
$z_{jk}^{[l]}$ 表示表示第 $l$ 层第 $j$ 个神经元的线性结果，同时也是该神经元激活函数的输入。
$a_j^{[l]}$ 表示第 $l$ 层第 $j$ 个神经元的激活函数输出。
σ 表示激活函数。
第 $l$ 层中第 $j$ 个神经元的激活为:
$$a_j^{[l]}=\sigma (z_j^{[l]})=\sigma (\sum _k{w}_{jk}^{[l]}{a}_k^{[l-1]}+b_j^{[l]})$$
$w^{[l]}$ 表示第 $l$ 层的权重矩阵。
$b^{[l]}$ 表示第 $l$ 层的偏置向量。
$a^{[l]}$ 表示第 $l$ 层的神经元向量。
结合上图所示：
$w^{[1]}=\left[\begin{array}{lll}{w}_{11}^{[1]}& w_{12}^{[1]}& \\ w_{21}^{[1]}& w_{22}^{[1]}& \\ w_{31}^{[1]}& w_{32}^{[1]}& \end{array}\right]$
$w^{[2]}=\left[\begin{array}{lll}{w}_{11}^{[2]}& w_{12}^{[2]}& w_{13}^{[2]}\\ w_{21}^{[2]}& w_{22}^{[2]}& w_{23}^{[2]}\end{array}\right]$
$b^{[1]}=\left[\begin{array}{l}{b}_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\end{array}\right]$
$b^{[2]}=\left[\begin{array}{l}{b}_1^{[2]}\\ b_2^{[2]}\end{array}\right]$
进行线性矩阵运算：
$z^{[1]}=w^{[1]}\ast a^{[0]}+b^{[1]}=\left[\begin{array}{lll}{w}_{11}^{[1]}& w_{12}^{[1]}& \\ w_{21}^{[1]}& w_{22}^{[1]}& \\ w_{31}^{[1]}& w_{32}^{[1]}& \end{array}\right]\cdot \left[\begin{array}{c}{a}_1^{[0]}\\ a_2^{[0]}\end{array}\right]+\left[\begin{array}{l}{b}_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\end{array}\right]=\left[\begin{array}{c}{w}_{11}^{[1]}{a}_1^{[0]}+w_{12}^{[1]}{a}_2^{[0]}+b_1^{[1]}\\ w_{21}^{[1]}{a}_1^{[0]}+w_{22}^{[1]}{a}_2^{[0]}+b_2^{[1]}\\ w_{31}^{[1]}{a}_1^{[0]}+w_{32}^{[1]}{a}_2^{[0]}+b_3^{[1]}\end{array}\right]$
那么，前向传播过程可以表示为：
$$a^{[l]}=\sigma \left(w^{[l]}{a}^{[l-1]}+b^{[l]}\right)$$
上述讲述的前向传播过程，输入层只有1个列向量，也就是只有一个输入样本。对于多个样本，输入不再是1个列向量，而是m个列向量，每1列表示一个输入样本。m个$a^{[l-1]}$列向量组成一个m列的矩阵$A^{[l-1]}$。

$A^{[l-1]}=\left[\begin{array}{cccc}|& |& \cdots & |\\ a^{[l-1](1)}& a^{[l-1](2)}& \dots & a^{[l-1](m)}\\ |& |& \dots & |\end{array}\right]$

多样本输入的前向传播过程可以表示为：
$$\begin{array}{c}{Z}^{[l]}=w^{[l]}\cdot A^{[l-1]}+b^{[l]}\\ A^{[l]}=\sigma \left(Z^{[l]}\right)\end{array}$$
与单样本输入相比，多样本$w^{[l]}$和$b^{[l]}$的定义是完全一样的，不同的只是$Z^{[l]}$和$A^{[l]}$从1列变成m列，每1列表示一个样本的计算结果。

损失函数

在有监督学习的机器学习算法中，我们期望能够最小化每个样例的误差。在使用梯度下降算法等其他优化算法都会使用误差，而误差就是来自于损失函数。
损失函数用于单个训练样本，而成本函数是多个训练样本的平均损失，也就是成本函数是每个样本的成本总和的平均值。优化策略旨在最小化成本函数。
下面例举几个常用的损失函数:

回归问题

1. 绝对值损失函数($L_1$损失函数)：

$L(\hat{y},y)=|y-\hat{y}|$

$y$ 表示真实值或期望值，$\hat{y}$ 表示预测值

2. 平方损失函数($L_2$损失函数)：

$L(\hat{y},y)=(y-\hat{y}{)}^2$

$y$ 表示真实值或期望值，$\hat{y}$ 表示预测值

分类问题

交叉熵损失：

$L(\hat{y},y)=-y\log (\hat{y})-(1-y)\log (1-\hat{y})$

$y$ 表示真实值或期望值，$\hat{y}$ 表示预测值

反向传播

反向传播的基本思想：通过计算输出层与期望值之间的误差来调整网络中的权重，使得误差变小(最小化损失函数或成本函数)，反向传播基于四个基础等式。

假设函数的梯度

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。为了更快的逼近最优解，从梯度反方向计算能够使求解过程变得更快。
假设函数 $f:R^{n\times 1}\to R$ 将输入的列向量（$n\times 1$ ）映射为一个实数。那么，函数 $f$ 的梯度定义为：

${\nabla }_{x}f(x)=\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_1}\\ \frac{\partial f(x)}{\partial x_2}\\ ⋮\\ \frac{\partial f(x)}{\partial x_n}\end{array}\right]$
同理，假设函数 $f:R^{m\times n}\to R$ 将输入的矩阵（shape: $m\times n$ ）映射为一个实数。函数 $f$ 的梯度定义为：

${\nabla }_{A}f(A)=\left[\begin{array}{cccc}\frac{\partial f(A)}{\partial A_{11}}& \frac{\partial f(A)}{\partial A_{12}}& \dots & \frac{\partial f(A)}{\partial A_{13}}\\ \frac{\partial f(A)}{\partial A_{21}}& \frac{\partial f(A)}{\partial A_{22}}& \dots & \frac{\partial f(A)}{\partial A_{2n}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f(A)}{\partial A_{m1}}& \frac{\partial f(A)}{\partial A_{m2}}& \dots & \frac{\partial f(A)}{\partial A_{mn}}\end{array}\right]$

可以简化为：

${\left({\nabla }_{A}f(A)\right)}_{ij}=\frac{\partial f(A)}{\partial A_{ij}}$

反向传播公式推导（四个基础等式）

为了最小化误差，需要我们不断调整神经网络中的权重 $w$ 和偏置 $b$ 。我们使用梯度下降算法来逼近最优解，为此我们需要知道权重 $w$ 和偏置 $b$ 的梯度，也就是总误差对二者的偏导数$\frac{\partial L}{\partial b_j^{[l]}}$和$\frac{\partial L}{\partial w_{jk}^{[l]}}$。
为了计算这些偏导数，引入一个中间变量 ${\delta }_j^{[l]}$，它表示网络中第 $l$ 层第 $j$ 个神经元的误差。反向传播能够计算出误差${\delta }_j^{[l]}$ ,再根据链式法则求出$\frac{\partial L}{\partial b_j^{[l]}}$和$\frac{\partial L}{\partial w_{jk}^{[l]}}$。
定义网络中第 $l$ 层第 $j$ 个神经元的误差为 ${\delta }_j^{[l]}$ :

${\delta }_j^{[l]}=\frac{\partial L\left(a^{[L]},y\right)}{\partial z_j^{[l]}}$

其中 $L$表示最后一层，也就是输出层，$L(a^{[L]},y)$ 表示损失函数，$y$ 表示真实值，$a^{[L]}$ 表示输出层的预测值。
每一层的误差向量可以表示为：

${\delta }^{[l]}=\left[\begin{array}{c}{\delta }_1^{[l]}\\ {\delta }_2^{[l]}\\ ⋮\\ {\delta }_n^{[l]}\end{array}\right]$
下面正式推导四个基本公式：

公式一 输出层误差

$${\delta }_j^{[L]}=\frac{\partial L}{\partial a_j^{[L]}}{\sigma }^{\prime }\left(z_j^{[L]}\right)$$
L表示输出层层数。以下用 $\partial L$ 表示 $\partial L\left(a^{[L]},y\right)$

写成矩阵形式是：

${\delta }^{[L]}=\left[\begin{array}{c}\frac{\partial L}{\partial a_1^{[L]}}\\ \frac{\partial L}{\partial a_2^{[L]}}\\ ⋮\\ \frac{\partial L}{\partial a_j^{[L]}}\end{array}\right]\odot \left[\begin{array}{c}{\sigma }^{\prime }\left(z_1^{[L]}\right)\\ {\sigma }^{\prime }\left(z_2^{[L]}\right)\\ ⋮\\ {\sigma }^{\prime }\left(z_j^{[L]}\right)\end{array}\right]$

表示成公式：
$${\delta }^{[L]}={\nabla }_{a}L\odot {\sigma }^{\prime }\left(z^{[L]}\right)$$

公式一 推导过程

由上图所示，该图中只有一个输出只有一个神经元，具体问题中可能有多个输出神经元。成本函数是每个输出神经元的损失函数之和，每个输出神经元的误差与其它神经元没有关系。
计算输出层的误差 ${\delta }_j^{[L]}=\frac{\partial L}{\partial z_j^{[L]}}$ ，根据链式法则
${\delta }_j^{[L]}=\frac{\partial L}{\partial a_j^{[L]}}\frac{\partial a_j^{[L]}}{\partial z_j^{[L]}}$
$\sigma$ 表示激活函数，由$a_j^{[L]}=\sigma \left(z_j^{[L]}\right)$，计算出 $\frac{\partial a_j^{[L]}}{\partial z_j^{[L]}}={\sigma }^{\prime }\left(z_j^{[L]}\right)$ ，代入最后得到

${\delta }_j^{[L]}=\frac{\partial L}{\partial a_j^{[L]}}{\sigma }^{\prime }\left(z_j^{[L]}\right)$
最后再向量化：
${\delta }^{[L]}={\nabla }_{a}L\odot {\sigma }^{\prime }\left(z^{[L]}\right)$

公式二 隐藏层误差

这里有混淆的地方，我们先提前假设以下，以免下面为什么权重矩阵转置了产生疑惑。
第$(l)$层一共有$j$个神经元，第$(l+1)$层一共有$k$个神经元，那么前向传播的权重矩阵为：$(k,j)$
$$\begin{array}{c}{\delta }_j^{[l]}={\sum }_k{w}_{kj}^{[l+1]}{\delta }_k^{[l+1]}{\sigma }^{\prime }\left(z_j^{[l]}\right)\end{array}$$
写成矩阵形式：

${\delta }^{[l]}=\left[\begin{array}{l}\left[\begin{array}{lllc}{w}_{11}^{[l]}& w_{12}^{[l]}& \dots & w_{1k}^{[l]}\\ w_{21}^{[l]}& w_{22}^{[l]}& \dots & w_{2k}^{[l]}\\ ⋮& ⋮& \ddots & ⋮\\ w_{j1}^{[l]}& w_{j2}^{[l]}& \dots & w_{jk}^{[l]}\end{array}\right]\left[\begin{array}{c}{\delta }_1^{[l+1]}\\ {\delta }_2^{[l+1]}\\ ⋮\\ {\delta }_k^{[l+1]}\end{array}\right]\end{array}\right]\odot \left[\begin{array}{c}{\sigma }^{\prime }\left(z_1^{[l]}\right)\\ {\sigma }^{\prime }\left(z_2^{[l]}\right)\\ ⋮\\ {\sigma }^{\prime }\left(z_j^{[l]}\right)\end{array}\right]$
矩阵形状：(j,k) * (k,1) $\odot$ (j,1) = (j,1)

权重矩阵的形状从(k,j)转置变成(j,k)。

表示成公式：
$${\delta }^{[l]}=\left[w^{[l+1{]}^T}{\delta }^{[l+1]}\right]\odot {\sigma }^{\prime }\left(z^{[l]}\right)$$

公式二 推导过程

$z_k^{[l+1]}={\sum }_j{w}_{kj}^{[l+1]}{a}_j^{[l]}+b_k^{[l+1]}={\sum }_j{w}_{kj}^{[l+1]}\sigma \left(z_j^{[l]}\right)+b_k^{[l+1]}$
对 $z_j^{[l]}$ 求偏导：
$\frac{\partial z_k^{[l+1]}}{\partial z_j^{[l]}}=w_{kj}^{[l+1]}{\sigma }^{\prime }\left(z_j^{[l]}\right)$
根据链式法则：
${\delta }_j^{[l]}=\frac{\partial L}{\partial z_j^{[l]}}={\sum }_k\frac{\partial L}{\partial z_k^{[l+1]}}\frac{\partial z_k^{[l+1]}}{\partial z_j^{[l]}}={\sum }_k{w}_{kj}^{[l+1]}{\delta }_k^{[l+1]}{\sigma }^{\prime }\left(z_j^{[l]}\right)$

公式三 参数变化率

为了避免和公式二混淆，提前假设：第$(l-1)$层一共有$k$个神经元，第$(l)$层一共有$j$个神经元，那么前向传播的权重矩阵为：$(j,k)$
$$\begin{array}{c}\frac{\partial L}{\partial b_j^{[l]}}={\delta }_j^{[l]}\\ \frac{\partial L}{\partial w_{jk}^{[l]}}=a_k^{[l-1]}{\delta }_j^{[l]}\end{array}$$
写成矩阵形式：
$\frac{\partial L}{\partial b^{[l]}}=\left[\begin{array}{c}{\delta }_1^{[l]}\\ {\delta }_2^{[l]}\\ ⋮\\ {\delta }_j^{[l]}\end{array}\right]={\delta }^{[l]}$
矩阵形状：(j,1)

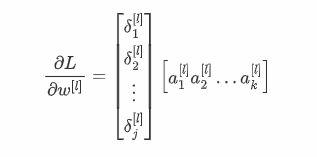
矩阵形状：(j,1) * (1,k) = (j,k), 和 $w^{[l]}$ 的维度一致 。
表示成公式：

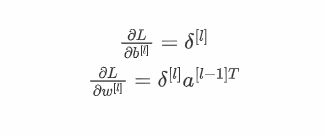
公式三 推导过程

$z_j^{[l]}={\sum }_k{w}_{jk}^{[l]}{a}_k^{[l-1]}+b_j^{[l]}$
L 对 $b_j^{[l]}$ 求偏导，根据链式法则得到

$\frac{\partial L}{\partial b_j^{[l]}}=\frac{\partial L}{\partial z_j^{[l]}}\frac{\partial z_j^{[l]}}{b_j^{[l]}}=\frac{\partial L}{\partial z_j^{[l]}}\ast 1={\delta }_j^{[l]}$

L 对 $w_{jk}^{[l]}$ 求偏导，根据链式法则得到

$\frac{\partial L}{\partial w_{jk}^{[l]}}=\frac{\partial L}{\partial z_j^{[l]}}\frac{\partial z_j^{[l]}}{w_{jk}^{[l]}}=a_k^{[l-1]}{\delta }_j^{[l]}$

公式四 参数更新

根据梯度下降法原理，朝着梯度的反方向更新参数
$$\begin{array}{c}{b}_j^{[l]}\leftarrow b_j^{[l]}-\alpha \frac{\partial L}{\partial b_j^{[l]}}\\ w_{jk}^{[l]}\leftarrow w_{jk}^{[l]}-\alpha \frac{\partial L}{\partial w_{jk}^{[l]}}\end{array}$$
写成矩阵形式：
$$\begin{array}{l}{b}^{[l]}\leftarrow b^{[l]}-\alpha \frac{\partial L}{\partial b^{[l]}}\\ w^{[l]}\leftarrow w^{[l]}-\alpha \frac{\partial L}{\partial w^{[l]}}\end{array}$$
这里的 $\alpha$ 指的是学习率。学习率决定了反向传播过程中梯度下降的步长。

BP神经网络注意事项

1.权重矩阵的初始化，不能都初始化为0，会使整个模型变成无效的线性运算，具体原因自行查找。
2.对于多分类问题，一般是分几类就设计几个输出神经元。假设分四类，就设置四个神经元，（1，0，0，0） （0，1，0，0）（0，0，1，0）（0，0，0，1）。