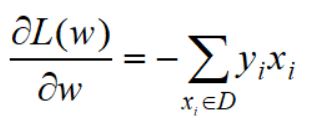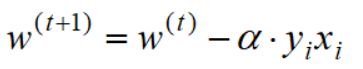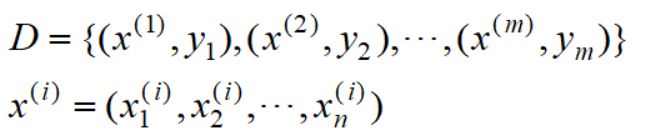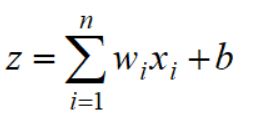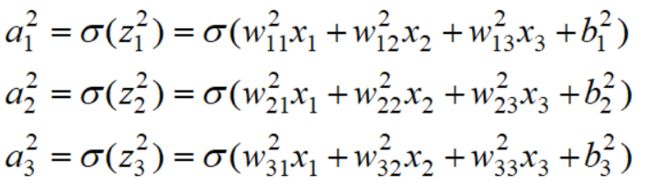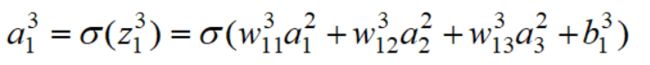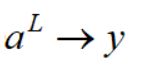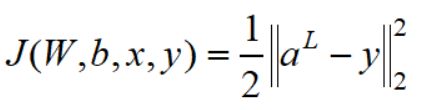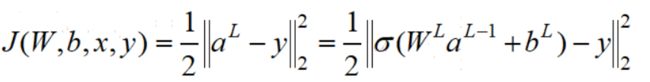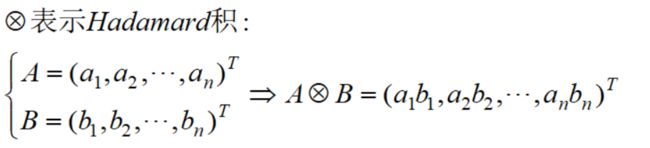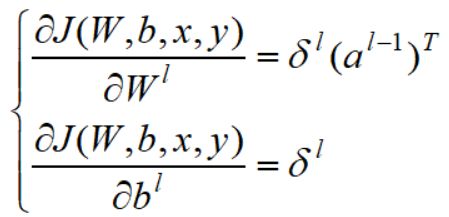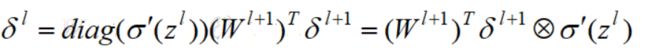多层感知机（MLP）

1.多层感知机(MLP)是深度神经网络(DNN)的基础算法,有时候提起DNN就是指MLP

2.感知机跟SVM优化的目标一致，损失函数不同(前者分母限制为1，后者分子限制为1)

3.神经网络由输入层(第一层)、隐藏层(中间层)和输出层(最后一层)构成

4.在MLP中,层与层之间是全连接的

5.前向传播算法用于求解相邻两层间输出的关系,某层的输入就是上一层的输出

6.反向传播算法(BP)用于求解各层的系数关系矩阵W和偏倚向量b

7.求解MLP采取梯度下降法

多层感知机（Multi-Layer perceptron,MLP），是深度神经网络（Deep Neural Networks，DNN）的基础算法，因此有时候说DNN就是指多层感知机。

我们在感知机与线性判别分析一文中简要提到了感知机的思想——错误驱动。为了更好介绍多层感知机，先回顾一下感知机算法。

感知机

感知机的损失函数为

注：这里的i代表第i个样本

它的梯度为：

采取随机梯度下降法求解，每次仅采用一个错误样本，则梯度迭代公式为：

由此我们得到感知机的算法流程：

拓展

在面试的时候，可能会碰到面试官问感知机算法与支持向量机（SVM）的区别，这里做一个简要拓展。

实际上，无论是SVM还是感知机，都是优化目标函数：

一个超平面乘以一个常数不会改变超平面，在感知机里把分母限制到1，而在SVM里把分子限制到1。本质上它们优化的目标是一致的，只是损失函数不同，这跟后面的优化算法有关系。

引出神经网络

为了更好介绍神经网络。我们对记号做一个调整。设有m个n维数据集D：

用下标代表第几个维度，上标代表第几个样本。

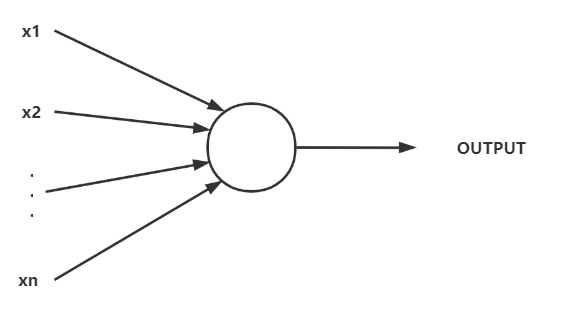
感知机模型可以看成由若干个输入和一个输出的模型：

输入与输出之间要学习一个线性关系（回顾广义线性模型），得到中间输出结果：

然后引入一个激活函数（神经元）：

这样就得到了分类标签1或-1

而神经网络是在感知机上做拓展：

• 加入隐藏层(可以有多个),增强模型表达能力

• 输出层拓展到多个，能应用到分类回归上

• 对激活函数做拓展，不限制sign形式

神经网络层可以分为输入层，隐藏层和输出层三层。一般来说第一层是输入层，最后一层是输出层，而中间的都是隐藏层，且层与层之间是全连接的：

从每一个局部来看，都是一个线性模型加上一个激活函数。

接下来看看在神经网络里面，变量系数w和偏倚项b是如何定义的。先给结论：

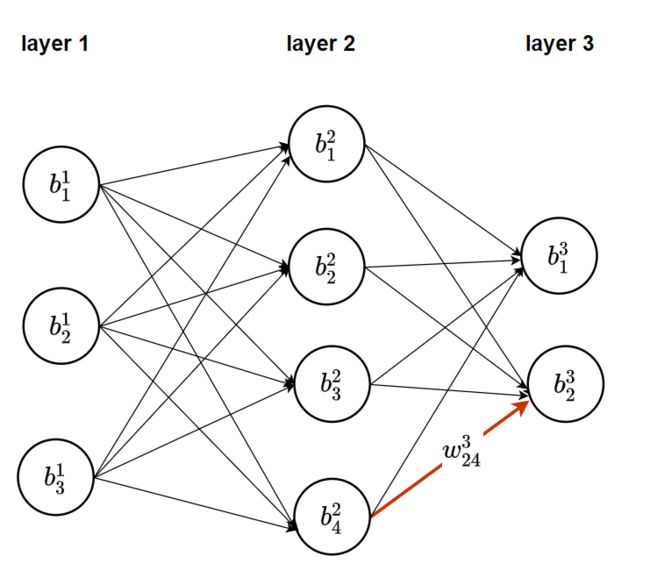
比如对于下图三层的DNN：

可以知道，上标代表所在的层数，下标的第一个数字代表所在层数的索引，下标第二个数字代表所在上一层的索引；偏倚项只在该层起作用，所以下标就代表该层的索引。

另外，我们用z代表每一层的线性表示，用a代表每一层的输出（加上激活函数），他们的上下标命名原则与变量系数一致。由DNN结构可以知道，下一层的输入就是上一层的输出。

最后提一点，输入层是没有偏倚项的

前向传播

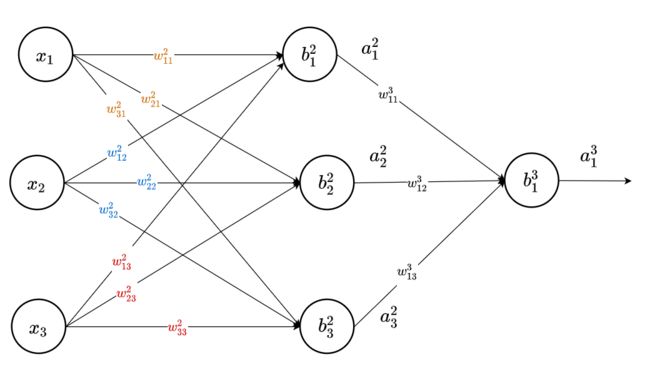
DNN是层层输出的，显然我们想利用上一层的输出计算下一层的输出，假设激活函数为σ(z)，对于下图的神经网络

对于第二层，它的输入是第一层初始变量x，所以输出为：

对于第三层，它的输入是第二层的输出，所以第三层的输出为：

由上面的例子我们很自然的就想到用矩阵的方式表达输入与输出的关系。

由此我们可以得到多层感知机的前向传播算法：

反向传播

数学模型最终是希望预测的结果与真实接近，在MLP中，我们希望

引入损失函数来衡量模型好坏，此处采取均方误差为损失函数：

对于第L层，我们有

代入损失函数，有：

采取梯度下降法迭代，为了表示方便，我们引入Hadamard积：

J关于W,b的梯度为：

它们有公共部分，把公共部分表示出来：

于是第L层的W,b梯度可以表示为：

对于任意的第l层呢，幸运的是，它们的结果类似：

又因为

所以考虑递推法得到所有层的δ，根据

得到l层与l+1层的递推公式：

综合以上，我们可以得到多层感知机的反向传播算法（BP）：

参考资料：

https://www.cnblogs.com/pinard/p/6418668.html