PyTorch手动实现线性回归

目标

1. 知道requires_grad的作用
2. 知道如何使用backward
3. 知道如何手动完成线性回归

1. 前向计算

对于pytorch中的一个tensor，如果设置它的属性.requires_grad为True，那么它将会追踪对于该张量的所有操作。或者可以理解为，这个tensor是一个参数，后续会被计算梯度，更新该参数。

1.1 计算过程

假设有以下条件（1/4表示求均值，x_i中有4个数），使用torch完成其向前计算的过程

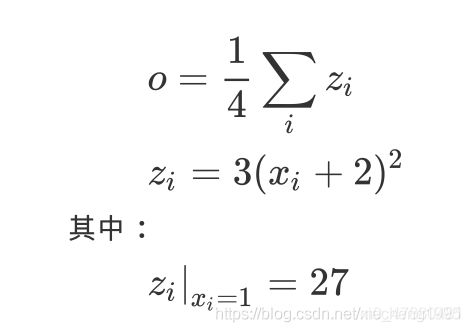
如果x为参数，需要对其进行梯度的计算和更新

那么，在最开始随机设置x的值的过程中，需要设置他的requires_grad属性为True，其默认值为False

import torch 
x = torch.ones(2, 2, requires_grad=True) #初始化参数x，并设置requires_grad=True用来追踪其计算历史
print(x)
 
#tensor([[1., 1.],
# 		 [1., 1.]], requires_grad=True)

y = x+2
print(y)
#tensor([[3., 3.],
# 		 [3., 3.]], grad_fn=)
 
z = y*y*3 #平方x3
print(z)
#tensor([[27., 27.],
# 		 [27., 27.]], grad_fn=)
 
out = z.mean() #求均值
print(out)
#tensor(27., grad_fn=)

从上述代码可以看出：

1. x的requires_grad属性为True
2. 之后的每次计算都会修改其grad_fn属性，用来记录做过的操作。通过这个函数和grad_fn能够组成一个和前一小节类似的计算图

1.2 requires_grad和grad_fn

a = torch.randn(2, 2) 
a = ((a * 3) / (a - 1))
print(a.requires_grad) # False
a.requires_grad_(True) # 就地修改
print(a.requires_grad) # True
b = (a * a).sum()
print(b.grad_fn) # 
with torch.no_gard():
    c = (a * a).sum() # tensor(151.6830),此时c没有gard_fn

print(c.requires_grad) #False

注意：

为了防止跟踪历史记录（和使用内存），可以将代码块包装在with torch.no_grad():中。在评估模型时特别有用，因为模型可能具有requires_grad = True的可训练的参数，但是我们不需要在此过程中对他们进行梯度计算。

2. 梯度计算

对于1.1中的out而言，我们可以使用backward方法来进行反向传播，计算梯度out.backward()，此时便能够求出导数dout/dx，调用x.grad能够获取导数值，得到

tensor([[4.5000,4.5000],
		[4.5000,4.5000]])

因为

在x_i等于1时其值为4.5

注意：在输出为一个标量的情况下，我们可以调用输出tensor的backward() 方法，但是在数据是一个向量的时候，调用backward()的时候还需要传入其他参数。（很多时候我们的损失函数都是一个标量，所以这里就不再介绍损失为向量的情况。）

loss.backward()就是根据损失函数，对参数（requires_grad=True）的去计算他的梯度，并且把它累加保存到x.gard，此时还并未更新其梯度。所以每次计算梯度前，先对之前计算的梯度进行置零操作。

注意点：

1. tensor.data：

• 在tensor的require_grad=False，tensor.data和tensor等价
• require_grad=True时，tensor.data仅仅是获取tensor中的数据

2. tensor.numpy():

• require_grad=True不能够直接转换，需要使用tensor.detach().numpy()

简单总结：

3. 线性回归实现

下面，我们使用一个自定义的数据，来使用torch实现一个简单的线性回归

假设我们的基础模型就是y = wx+b，其中w和b均为参数，我们使用y = 3x+0.8来构造数据x、y，所以最后通过模型应该能够得出w和b应该分别接近3和0.8

1. 准备数据
2. 计算预测值
3. 计算损失，把参数的梯度置为0，进行反向传播
4. 更新参数

课件中的源代码：

import torch
import numpy as np
from matplotlib import pyplot as plt

#1. 准备数据 y = 3x+0.8，准备参数 
x = torch.rand([50])
y = 3*x + 0.8
 
w = torch.rand(1,requires_grad=True)
b = torch.rand(1,requires_grad=True)

def loss_fn(y,y_predict): 
	loss = (y_predict-y).pow(2).mean()
	for i in [w,b]:
		# 每次反向传播前把梯度置为0
		if i.grad is not None:
			i.grad.data.zero_()
	# [i.grad.data.zero_() for i in [w,b] if i.grad is not None]
	loss.backward()
	return loss.data
 
def optimize(learning_rate): 
	# print(w.grad.data,w.data,b.data)
	w.data -= learning_rate* w.grad.data
	b.data -= learning_rate* b.grad.data

for i in range(3000):
	#2. 计算预测值
	y_predict = x*w + b

	#3.计算损失，把参数的梯度置为0，进行反向传播
	loss = loss_fn(y,y_predict)

	if i%500 == 0:
		print(i,loss)
	
	#4. 更新参数w和b
	optimize(0.01)

# 绘制图形，观察训练结束的预测值和真实值
predict = x*w + b #使用训练后的w和b计算预测值

plt.scatter(x.data.numpy(), y.data.numpy(),c = "r")
plt.plot(x.data.numpy(), predict.data.numpy())
plt.show()
 
print("w",w)
print("b",b)

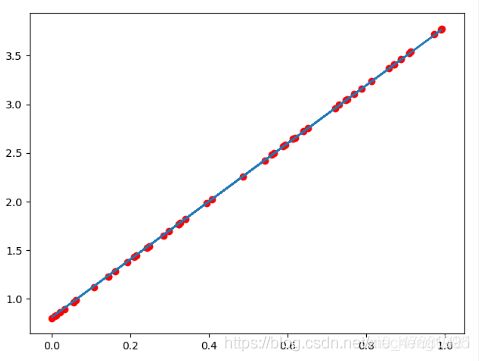
图形效果如下：

打印w和b，可有

w tensor([2.9280], requires_grad=True)
b tensor([0.8372], requires_grad=True)

可知，w和b已经非常接近原来的预设的3和0.8

补充上课老师手敲代码(个人认为比课件中给的清晰)：

import torch
from matplotlib import pyplot as plt

learing_rate = 0.01

# 1. 准备数据
# y = 3x+0.8
x = torch.randn([500, 1])
y_true = 3*x+0.8

# 2. 通过模型计算y_predict
w = torch.rand([1, 1], requires_grad=True)
b = torch.tensor(0, requires_grad=True, dtype=torch.float32)

# 4. 通过循环，反向传播，更新参数
for i in range(800):
    # 3. 计算loss
    y_pred = w * x + b
    loss = (y_pred-y_true).pow(2).mean()

    if w.grad is not None:
        w.grad.data.zero_()
    if b.grad is not None:
        b.grad.data.zero_()

    loss.backward()  # 反向传播
    w.data = w.data - learing_rate*w.grad.data
    b.data = b.data - learing_rate*b.grad.data
    if i % 50 == 0:
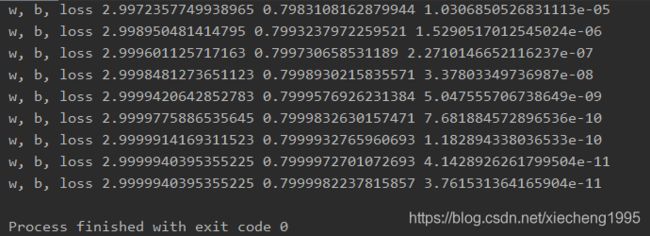
        print("w, b, loss", w.item(), b.item(), loss.item())

plt.figure(figsize=(20, 8))
plt.scatter(x.numpy().reshape(-1), y_true.numpy().reshape(-1), c='r')
y_pred = w * x + b
plt.plot(x.numpy().reshape(-1), y_pred.detach().numpy().reshape(-1))
plt.show()

运行结果：

视频参考：https://www.bilibili.com/video/BV1pi4y1x7fx?p=13