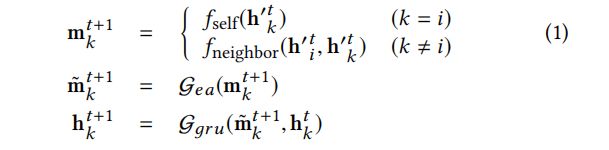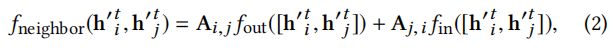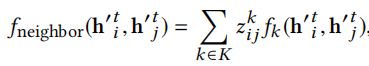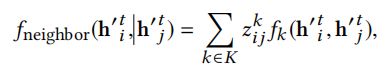基于图神经网络的知识追踪
（持续更新ing）
github源码：https://github.com/jhljx/GKT
Interaction Networks for Learning about Objects, Relations and Physics Code
Relational inductive biases, deep learning, and graph networks（关系归纳偏差，深度学习和图网络） code
Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation code
Inductive Representation Learning on Large Graphs (从大图中学习归纳表示) code
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
目录
知识追踪 —— 使用图神经网络对学生知识点熟练度建模
(将学生的知识点掌握程度基于时间进行建模，用来预测学生随着时间做对练习题的概率)
1、背景介绍
2、知识追踪
3、GNN
4、基于图模型的知识追踪
4.1问题定义
4.2 解决方法
4.3 实现潜在的图结构和任意函数
4.4 同之前方法的比较
5、实验
5.1 数据集
5.2实现细节
5.3 预测性能
5.4 预测的可解释性
5.5 网络分析
6、合并Richer_GNN架构
知识追踪 —— 使用图神经网络对学生知识点熟练度建模
(将学生的知识点掌握程度基于时间进行建模，用来预测学生随着时间做对练习题的概率)
1、背景介绍
在智慧教育系统（E-learning 系统）上，学生的表现可以随着时间逐渐被预测，正确的预测能够帮助学生准确选择和现在认知水平相当的试题，这种电子学习平台可以帮助学生提高学习积极性，目前有很多知识追踪的方法，最近提出有：DKT（使用了RNN模型），这个方法证明比之前的方法都要好，从数据结构的角度来看，课程学习也可以被建模成图模型，将熟练掌握一个知识概念，所需要掌握的知识点建模成图上的点，并且这些知识点之间是互相关联的。众所周知，将关于数据的图结构性质的先验知识引入模型可以提高模型的性能和可解释性。
如：将一个知识概念拆分为三个知识点，表示为 V={v1,v2,v3}，并且掌握v1，就必须要掌握知识点v2,同时，掌握知识点v2,也必须要掌握v3 (比如要解决二元一次方程就必须会解一元一次方程，要解决一元一次方程就必须会移项)，因此结合图结构的知识点模型，可以有效地提高知识追踪模型，然而DKT并没有考虑到知识点之间地这种关系，以往基于深度学习地方法（如RNN）的体系结构，通常对序列数据表现良好，但是不能有效地处理图形结构的数据。
最近，基于图神经网络的研究兴起，虽然在这种不规则的域上操作数据，对现有的及其学习方法提出了挑战，各种泛化框架和重要操作在多个研究中也取得了比较好的结果，GNN从关系归纳偏差的角度出发，结合人类对数据本质的先验知识，提高了机器学习模型的效率，这部分，Battaglia等人认为是可解释的。GNN可以找到潜在的知识结构，但问题也在这，在知识追踪中使用图神经网络的时候，如何表示潜在知识结构是很困难的，GNN对于图形结构数据的建模具有相当大的表达能力。这篇论文，我们将其重新定义为一个GNN应用程序，并提出了一个新的模型，可以在考虑潜在知识结构的情况下预测学生知识掌握程度
在一些知识追踪的案例中，知识点之间的关系和关系的强度，没有明确的提供，对于人类专家来说，启发式和手动注释内容关系是必要的，但是需要有领域专家花费大量时间才可以完成。所以很难提前将所有的知识都进行知识点图建模，我们把这种问题定义为隐藏的图结构问题，像概念回答转移概率，另外一个解决方案是在学习图结构本身的同时优化主要任务，最近关于GNN研究中，相关的话题就是图的边（知识点关系）的学习。
这篇论文，主要提出了基于图神经网络的图知识追踪，将知识追踪重新定义为GNN中的时间序列节点级分类问题。这种构想是基于3种假设：1.课程知识被分解为指定数目的知识点 2.学生目前是有指定的知识掌握程度，设为（knowledge state）3. 课程知识被建模为一个图，这个图用来更新学生的知识点掌握程度，当学生答对/答错一道题，那么学生的认知状态受影响的不仅仅是这道题的知识点，还有这个知识点相关的其他知识点，也就是邻接点。
数据集使用的是两个开放的数学联系日志数据集的子集，对这个方法进行了实例验证，在预测性能上面，我们的模型比以往的基于深度学习的模型表现要优，这意味着我们的模型在改善学生成绩预测上面有很大的潜力。此外，通过对训练模型的预测模式的分析，可以从模型的预测中清楚地解释学生熟练程度的过程，即学生所理解的概念及其所需的时间，而以往的方法解释能力较差。这意味着我们的模型比以前的模型提供了更多可解释的预测。在假设目标课程是图结构的情况下，跟踪实际教育环境中的应用，所得结果都验证了我们的模型在提高知识的性能和适用性方面的潜力。
贡献如下：
我们证明了将图神经网络应用在知识追踪中，提高了学生学习成绩预测的性能，不需要任何附加的信息，在更加精准的内容个性化下，学生可以有效地掌握课程知识。平台可以提供更高质量的服务来维护用户的高参与度。
我们的模型提高了模型预测的可解释性。教师和学生可以更准确地识别学生的知识状态，通过理解推荐练习的原因，学生可以更积极地进行推荐练习。E-learning平台和教师可以通过分析学生的失败点来更容易地重新设计课程。
为了解决隐式图结构问题，我们提出各种实现方式，并通过实验验证其有效性。不需要专家花费大量的精力，对概念之间的关系进行的注释。教育专家可以有一个新的标准来考虑什么良好的知识结构是对课程的改进设计。
2、知识追踪
Xt 表示在时间t时刻是否正确回答一系列问题q（向量） 的概率 r，yt是学生在下个时间 t+1正确回答每个练习 的概率，KT是知识追踪模型。Since Piech等人第一次提出以深度学习为基础来做知识追踪，并且也证明了RNN的强大的解释能力，后续的研究都采用RNN或者其拓展知识来做知识追踪，这个模型定义了一个隐藏的状态，或者是学生当前的一个知识储备状态
，并且随着学生做题的状态不断地更新，以RNN为代表地模型，定义了一个固定长度的向量X，Xt由两种离散的值0和1表示，0表示题目做错，1表示题目做对，训练目标是最小化模型下观察到的学生反应序列的负对数似然（NLL）。
3、GNN
GNN（Graph Nueral network）图神经网络是一种作用在图数据上的神经网络，虽然表示图数据很复杂，但是它的超强解释性还是吸引了很多人对此投入研究，对GNN的研究兴趣有很大一部分原因是来自CNN,CNN可以摘录多尺度局部空间特征及其组合构造表现力，从而在各种研究领域，如计算机视觉。然而，CNNs只能对常规的欧几里德数据（如图像和文本)，而现实世界中的一些应用程序生成非欧几里德数据。另一方面，GNN将这些非欧几里德数据结构视为图形，并使CNN的相同优点也能反映在这些高度多样化的数据上。巴塔利亚等人从关系归纳偏置的角度解释了GNN和CNN的这种表达能力，通过融合人类对数据本质的先验知识，提高了机器学习模型的样本效率。
在GNN的几个研究课题中，边缘特征学习是与我们工作最相关的。图形注意力网络（GATs）将多头部注意力机制应用于GNN，并在训练过程中学习边缘权值，而不需要预先定义它们。神经关系推理（NRI）利用变分自动编码器（VAE）以无监督的方式学习潜在的图结构。我们的方法假设一个课程的知识概念的潜在的图结构，并使用图形运算符来模拟学生随着时间对于知识点的熟练度变化。然而，在许多情况下，图结构本身并没有显式地提供。我们通过设计模型来解决这个问题，这些模型学习边连接本身，同时优化学生的表现，通过扩展这些边缘特征学习进行预测机制。我们请在第3.3节对此进行详细解释。
4、基于图模型的知识追踪
4.1问题定义
将一门知识建模为图，要熟练掌握这个知识，需要掌握很多子知识点，这里知识定义为 G = (V,E) , 知识点为 {v1,v2,v3....vN} ，这些子知识点之间的关系定义为边E(edge)，其中 
，学生当前的知识点熟练度建模为
表示学生在t时刻，对于知识点v的掌握程度，并且这个掌握程度是随着时间而变化的，当学生回答了包含知识点vi的题目时候，与vi相关的
,就会更新，并且与v相关的邻接知识点
也会更新，Ni表示vi的所有相连的知识点
4.2 解决方法
GKT将GNN应用于知识跟踪任务，并利用知识的图结构特性。我们在图1中展示了GKT的体系结构。以下段落详细解释了这些过程。
4.2.1 聚合，首先，该模型集合了所回答的概念i及其邻近概念j∈Ni的隐藏状态和嵌入
，X表示对每一道题回答的结果的记录，是一个输入向量，
是一个矩阵，嵌入了知识点的下标和的反馈，
表示每个知识点的下标，
表示知识点矩阵的第K行，并且e是embeeding的大小。
4.2.2 更新。接下来将根据已经聚合的特征和知识图架构来更新整个知识的结构图
是一个多层的感知器，
是一个擦除-添加门，
是一个门控递归单元，
表示任意函数，用来表示基于知识图谱结构将信息传送到邻接结点，我们在3.3节提出不同的实现方法。
4.2.3 预测。最后，这个模型输出的是，每个学生在下一个时间点正确回答每个知识点的预测概率。
Wout是每个节点的公共权重矩阵，bk是节点k的偏置项，
是sigmoid函数，训练模型来最小化观测到的NLL的值。我们可以用边缘信息，从邻接的知识点中收集学生的知识掌握程度。我们验证了，基于目标学生知识状态
来预测
是更好的一种预测方式，所以我们只使用更新过的学生认知状态。
4.3 实现潜在的图结构和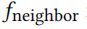任意函数
GKT能够利用知识本质的图结构来进行知识追踪，但在大多数情况下，这种结构并没有给出，为了实现这种图结构和，我们介绍两种方法。
4.3.1 基于统计的方法，这种方法实现了基于一定统计量的邻接矩阵A，并且将这种方法应用到了
这里
和
都是多层感知机，这里介绍三种类型的图结构
（1）Dense graph 是一个紧密连接的图
（2）Transition graph 是一个转变概率矩阵，当i <> j，Ai,j = 
，否则 就是 0. 
表示在概念i被回答后，j立马被回答的次数。
（3）DKT graph 基于被训练好的DKT模型的条件预测概率而生成的图。
GKT模型的架构，当学生回答了某一个知识点时，GKT首先聚合与其相关的知识点的特征，根据这些特征更新学生的认知状态，最后预测学生在下次正确回答这些知识点的概率。
4.3.2 基于学习的方法，在优化性能预测的同时，会同步学习到这种图结构，这里介绍三种图结构学习的方法。
（1）参数邻接矩阵（Parametric adjacency matrix PAM），简单地参数化邻接矩阵A，并且在一定条件下，用其他参数对其进行优化，比如A满足邻接矩阵，和公式2定义类似。
（2）多头机制 (Multi-head Attention MHA) ：利用多头注意力机制，依据两点之间的特征，推断两点之间关系（边）的权重。定义入下：
这里k是下标，标注是第k个head，
表示从点vi到点vj的第k个head的注意力权重，fk表示第k个head的注意力权重。
（3）变量自动编码器（Variational autoencoder VAE）假设表示边类型的离散变量，并使用点的特征来进行填充，定义入下：
共有k种边类型，
是从Gumbel-Softmax分布中采取的潜在变量，
是第k个边类型的神经网络，VAE用来最小化NLL和在编码分布q(z|x)和先验分布p(z)中的KL散度的，使用一个边类型来展示非边类型，表示在这种类型的边上不会有任何信息会被传递，在这种非边的类型上设置高概率会导致生成稀疏图。
这种学习方法接近于基于边的特征的学习策略，MHA和VAE分别受到了GAT和NRI的启发，然而，我们是基于两种方法来修改的，首先，我们根据静态特征而不是动态特征计算边缘权值，如概念和响应的嵌入。这使得知识图的结构不会随着学生和时间而改变，考虑到知识追踪的实质，这种方式是更好的。然后，依据VAE的说法，我们限制了每一个时刻里面的与答案相关的边类型的推测，这符合知识追踪的状况，学生在每一个时间段里面只需要回答一小部分的概念，这也使得计算成本从原始NRI的
降低到O(KN)。
我们会在5.1节讨论这三种方法的不同点
4.4 同之前方法的比较
可以从两个方面来进行比较，如图2
一个比较的点，是对学生当前认知水平的定义，
在DKT中，
表示单个隐藏的向量，并且每个知识状态都是相关的，但是，对每个概念的知识状态进行建模会变得复杂,导致长时间序列的性能下降，预测学生对于每一个知识点熟练度的可解释性变差，为了解决这些缺点，有人提出了动态键值记忆网络（Dynamic Key-Value memory network DKVMN）DKVMN使用了两种记忆矩阵，一种矩阵看作学生当前认知状态的栈，分别定义每个知识点，虽然这和GKT的概念差不多，但还是有些许差别，GKT是直接对每个知识点进行建模，而DKVMN则是定义了低维的潜在向量，再对它们的知识状态建模。
5、实验
5.1 数据集
这个实验我们使用了两个开放的学生数学练习日志数据集：在线教育服务ASSISTments的数据和KDDCU的用于教育数据挖掘挑战的数据。我们提供了表1中现有概念标签的示例。
使用某些条件对于数据进行预处理，对于ASSISTments数据集，将同时回答的日志组合成为一个，随后提取与命名概念标记关联的日志，最后提取回答了至少有10次的日志。对于KDDCup数据集，我们将问题和步骤的结合视为一个答案，然后抽取与概念标签相关的日志，最后抽取回答了至少有10次的日志。
将同步答案日志合并到一个集合中，可以防止不公平的高预测性能，因为频繁出现的标记，不包括概念***，每个概念标记的相应次数对日志进行阙值化，可以确保足够数量的日志来消除噪声。利用上述条件对数据集进行处理，最终在ASSISTments中获得了62，955条日志记录，包括1000个学生和101个知识点，在KDDCup数据集中获得了1000个学生和211个知识点。
5.2实现细节
每个数据集，都将学生的数据分成：训练、验证、测试三大块，所占比例分别为8：1：1，使用训练数据集来进行训练，用验证数据集来调整超参数。
DKT：根据Piech等人的研究，使用循环神经网络中的GRU来寻找超参数，隐藏层的大小为200，使用dropout为0.5的速率进行减枝，将变成
，批大小为32，使用Adam为优化器，学习速率为0.001
DKVMN：根据Zhang等人的研究，对ASSISTments数据集，内存槽的大小为20，隐藏向量的大小为32；对KDDCup数据集，内存槽的的大小为50，隐藏向量的大小为128；批大小为32，使用Adam为优化器，学习速率为0.001
GKT：所有的隐藏向量和嵌入层矩阵的大小为32，对于模型中的MLP，将隐藏向量的dropout下降为
5.3 预测性能
5.4 预测的可解释性
接下来，将GKT预测学生认知状态的过程进行可视化，并且评估模型预测的可解释性。可视化帮助学生以及老师发现过去的知识掌握情况，高效且直观，这是非常有必要的。
我们从两个角度来评估模型的可解释性。1、根据学生已经回答过的知识点，更新相关知识点的掌握情况 2、被更新的部分是根据知识点的结构图来调整的
以下步骤是分析整个知识点状态的变化过程
（1）在时间T之前，随机抽取学生的做题情况
（2）在训练模型的输出层，移除掉偏差向量。
（3）将学生的回答向量
输入到训练模型，并将输出向量
进行叠加
（4）将输出值进行正则化，结果控制在0到1之间
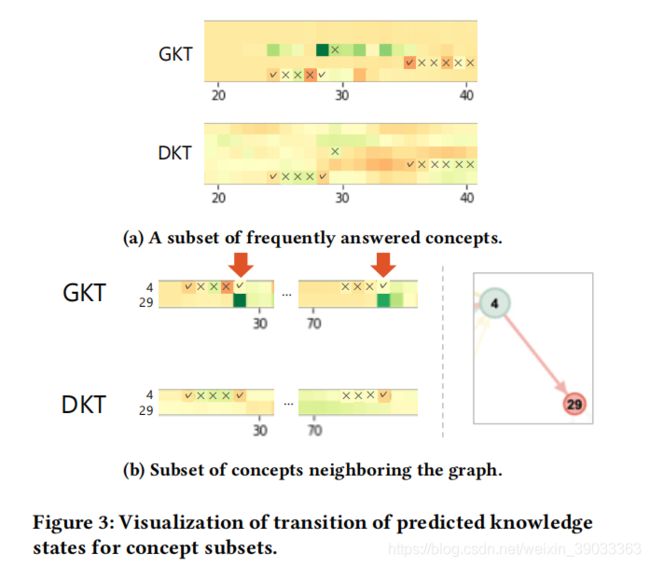
在图3a和图3b中，我们随机抽取了一名学生的做题日志，并以图的形式描绘了学生的知识状态，x轴表示时间，Y轴表示知识点，格子颜色表示学生知识点掌握的变化情况，红格子表示掌握程度降低，绿色表示掌握情况增加。
图3a表示GKT会更具知识点的相关性来更新学生的知识点掌握情况，而DKT依据模糊的依据将所有状态进行更新，在图3b中，能看到时间点28和75的时候，虽然知识点29没有被回答，但是因为和4有关，4有被回答，所以29的状态也被更新了。这表明GKT可以对学生的知识点掌握情况提供更明确和合理的解释。
5.5 网络分析
最后，从被训练的GKT模型中抽象出已经学习到的图结构，进行分析。在基于学习的方法中，GKT学习有助于预测学生表现的图形结构。 因此，从模型中提取的图显示了较高的预测性能，可以提供对良好知识结构的洞察。 图中描述了网络，其中左侧显示网络概述，右侧显示图形的本地连接。 节点的颜色是从蓝色到红色的，在那里，一个练习的答案越早，蓝色的是阴影。 节点的大小与它们的出度成正比，这意味着更大的节点会影响更多的节点。首先，在用于比较的可视化DKT图中，类似颜色的节点相互连接，从而生成集群。 当DKT用相同的单个隐藏向量对所有概念的隐藏状态进行建模时，对概念之间的存在长期依赖的建模是困难的。 因此，该模型倾向于学习以时间接近的顺序回答的节点之间的依赖关系。 从PAM中提取的图形表现出类似于DKT图的结构，其中构造了簇；从图形的右上角，我们可以看到一些几何概念是连接的。 从MHA 中提取的图显示了来自某些节点的几个即将到来的边缘。虽然模型可能已经了解了不同于其他图中概念之间的一些 特殊依赖关系，但它的预测可能是有偏差的。 因此，我们必须评估这种结构对预测性能的影响。 从VAE中提取的图与其他图不同，因为它形成了一个密集的图，其中几个节点相互连接。 虽然这些联系很多都很难解释，但从图的右下角，我们可以识别一些统计概念是连接的。
6、合并Richer_GNN架构
我们提出了第一种基于GNN的知识跟踪方法，并验证了相对 简单的体系结构。 在下面，我们讨论了三个方向来改进我 们的模型。 一种是根据节点的边缘类型对节点之间的信息传播施加适当的约束。 在本研究中，为了进行公平的比较，我们为基于统计的方法和基于学习的方法定义了两种类型的边缘。 然而，我们没有对每个节点类型施加任何约束；因此，对每个节点类型（如依赖方向和因果关系）的意义可能很小，特别是对于学习的边缘。 解决办法是根据节点的边缘类型对节点之间的信息传播施加一些约束例如定义边缘的方向，并将传播限制在从源节点到目标节点的一个方向上。 此外，这可 以作为关系归纳偏差，提高GKT的样本效率和可解释性。 另一个是将所有概念(如DKT)所共有的隐藏状态合并到GKT中。虽然只采用单个隐藏向量来表示学生知识状态，使DKT中概念之间复杂交互的建模复杂化，但将这种类型的表示添加到GKT中可以通过充当全局特征来提高性能。 全局特征意味着每个节点的共同特征，并且可以表示跨变量概念或学生原始概念的共同知识状态智力对个体概念理解的不变。最后一个可能的解决方案是实现多跳传播。 在本研究中，我们将传播限制在单个跳，即响应某个节点的信息只在一个时间步长传播到其相邻节点。 然而，要有效地模拟人类的学习机制，使用多跳将更合适。 此外，这可以使模型能够学习稀疏连接，因为模型可以将特征传播到远程节点，而不连接到其他节点。
深度学习的黑盒问题被人诟病已久，图神经网络的信息传播机制相较传统深度学习模型更具有可解释性。知识图谱提供了现实世界的事实知识，利用图神经网络模型尤其是概率图神经网络应用在知识图谱中实现逻辑推理，从而显式地生成基于知识图谱的推理路径，或许可以期待打开深度学习的黑盒。