深度学习基础--loss与激活函数--sigmiod与softmax;对数损失函数与交叉熵代价函数
sigmiod与softmax
sigmiod就是逻辑回归(解决二分类问题);softmax是多分类问题的逻辑回归
虽然逻辑回归能够用于分类,不过其本质还是线性回归。它仅在线性回归的基础上,在特征到结果的映射中加入了一层sigmoid函数(非线性)映射,即先把特征线性求和,然后使用sigmoid函数来预测。
sigmoid函数
当sigmoid函数作为神经元的激活函数时,有两种较好的损失函数选择:
1)sigmoid搭配方差代价函数(即采用均方误差MSE)。对于sigmoid,初始的误差越大,收敛得越缓慢。
2)sigmoid搭配交叉熵代价函数。它可以克服方差代价函数更新权重过慢的问题。
sigmiod的两端趋于平坦,导数中没有σ′(z)这一项,权重的更新是受σ(z)?y这一项影响,即受误差的影响。所以当误差大的时候,权重更新就快,当误差小的时候,权重的更新就慢。这是一个很好的性质。
Sigmoid 函数的物理含义
有两大关键的性质:易求导和连续性。
例子1
判断一个对象的分类时,很难做到 100% 的把握。所以,我们要算概率。为了方便讨论,只讨论 2 个分类的情况。
横坐标是测量值,纵坐标是概率。p 越大,属于 1 的概率越高,否则属于 0。
p = 0.5 是分界线,无法判断属于哪一个分类。
从 0.5 变到 0.6,基本可以认为属于分类 1,质的飞跃,虽然把握不大。0.6 -> 0.7, 非常重要的改进。从 0.9 变到 1,因为把握已经很大了,所以实际的帮助有限。
例子2
生物的种群增长。刚开始,种群的数量非常少,繁殖的速度会比较慢。随着数量的增加,繁殖速度越来越快。然后,食物不足,有天敌出现等原因。增速开始下降,最后稳定在一个区间内。而logistic 曲线非常好的描述了这个变化规律。
softmax
也是一种回归,CNN网络的最后一层采用softmax全连接(多分类时输出层一般用softmax)。softmax回归是logistic回归的多类别推广。
概念和性质
1)对概率分布进行归一化,使得所有概率之和为 1 。将一组数(一个一维向量)映射成一组范围为【0,1】的数,故向量的维度不变。
2)softmax 回归算法的代价函数 J(\theta),与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的 k 个可能值进行了累加。对于 J(\theta) 的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。
3)通过添加一个权重衰减项来修改代价函数,这个衰减项会惩罚过大的参数值。
注意:三个类别是互斥的时候,更适于选择softmax回归分类器 。而其他时候,建立三个独立的 logistic回归分类器更加合适。
Softmax Loss 和 Multiclass SVM Loss
参考资料:http://blog.csdn.net/u012767526/article/details/51396196
Softmax Loss:
给出 (xi,yi) ,其中 xi 是图像,yi 是图像的类别(整数),s=f(xi,W),其中s 是网络的输出,则定义误差如下:
P(Y=k|X=xi)=esk∑jesj
Li=−logP(Y=yi|X=xi)
例如:s=[3.2,5.1,−1.7],则p=[0.13,0.87,0.00] ,可得Li=−log(0.13)=0.89" "从误差的定义我们可以看出,Softmax在计算误差是考虑到了所有的类别的取值,因此,如果希望Softmax Loss尽可能的小,那么会导致其他类别的分数尽可能的低;
但是在SVM Loss(其实就是hing-loss)的定义中,我们可以看到,SVM Loss只考虑了那些在正确值附近或者压制了正确值的那些值,其他的均作为0处理,因此,SVM Loss更看重鲁棒性,只看重那些可能造成影响的点,这些所谓的可能造成影响的点也就是支持向量(现在你应该明白支持向量机是什么意思了);
但是,在分类问题中,这两种方法得到的结果往往都是一致的,所以我们也不需要担心太多。
SoftnaxWithLoss—softmax损失层
一般用于计算多分类问题的损失,在概念上等同于softmax层后面跟一个多变量的logistic回归损失层,但能提供更稳定的梯度。
对数损失函数(logarithmic loss function) 或对数似然函数
对数似然函数常用来作为softmax回归的代价函数。对应的,交叉熵代价函数常用来作为sigmoid回归的代价函数。
对数似然代价函数在二分类时可以化简为交叉熵代价函数的形式。
交叉熵代价函数(cross-entropy cost function)
是损失函数,它前面是概率(可以是sigmoid的输出,也可以是softmax的输出)。
参考资料:https://blog.csdn.net/chaipp0607/article/details/73392175
特性
1)非负性。(所以我们的目标就是最小化代价函数)
2)交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。
公式
假设概率分布p为期望输出(即标签label),概率分布q为实际输出,H(p,q)为交叉熵。
故在分类问题中,只有当x是label时,p=1,其余情况下p=0!
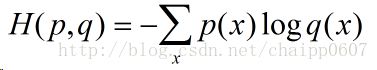

例如
softmax和交叉熵组合时,损失为softmax_cross_entropy(交叉熵)。
x = [[1, 2, 3],
[11, 7, 5]]
label = [2, 0]
则:
softmax(x) = [[0.09003057, 0.24472848,0.66524094],
[0.97962922, 0.01794253,0.00242826]]
softmax_cross_entropy(data, label) = - log(0.66524084) - log(0.97962922) = 0.4281871
具体的使用
在tensorflow中:
1)tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉熵。
2)tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉熵。
应用场景
当误差越大时,梯度就越大,参数w和b的调整就越快,训练的速度也就越快。
如果输出神经元是线性的,那么二次代价函数就是一种合适的选择。如果输出神经元是S型函数,那么比较适合用交叉熵代价函数。
具体来说,当sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数来替代方差代价函数(MSE),以避免训练过程太慢。
它可以克服方差代价函数更新权重过慢的问题(sigmiod的两端趋于平坦),导数中没有σ′(z)这一项,权重的更新是受σ(z)?y这一项影响,即受误差的影响。所以当误差大的时候,权重更新就快,当误差小的时候,权重的更新就慢。这是一个很好的性质。
cross-entropy loss与hinge loss
总而言之,cross-entropy loss比hinge loss要好!
1)cross-entropy的解释性强;通过作图可以看出, cross-entropy是平滑的;
2)hinge loss不是平滑的:hinge loss 对于正例的loss是0, 反例不是0, 这样导致其在每次迭代中, 只用到反例来更新模型(也就是只用了反例来建树, 丢失了正例的信息)
3)从它们的loss上看, cross-entropy loss对反例的惩罚是呈指数增长的, 而hinge loss是线性增长的。