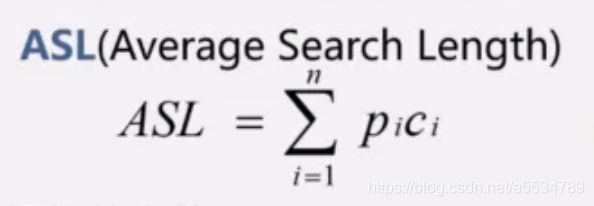数据结构与算法-线性表的查找【十八】
查找:
在特定的数据集合中,找到复合要求的数据。
查找的效率判断:
结构里面有一个专门的词汇,平均查找长度。通过这个关键指标去判断。
平均查找长度
关键字的平均比较次数,也称为平均查找长度。
查找到关键字的平均比较次数。【这个值越小查找效率越高】
n 为总记录的个数;
pi 查找到第i个记录的概率(通常pi就是1/n);
ci 找到第i个记录需要比较的次数;
线性表的查找
线性表的查找有三种:
- 顺序查找
- 折半查找(二分查找)
- 分块查找
下面分别介绍
1,顺序查找
线性表的存储结构可以是顺序存储【数组-下标】,也可以是链式存储
顺序查找的平均查找长度计算ASL=∑PiCi (i=1,2,3,…,n), Pi为1/n, Ci为比较次数。
查找成功的情况:最终的结果是1/n * (1+2+3...+n) 为 (n+1)/2。
查找成功的情况下,查找次数几乎为表长的一半。
代码:遍历数组,相等则返回,不等则返回-1。
优点 :对数据的顺序没有要求,逻辑简单,存储结构灵活,可以是顺序表存储,也可以是链表存储。
缺点 : ASL太长,时间效率不高。
2,折半查找(二分查找)
二分查找,每一次将查询的记录缩小一半。折半查找对数据的序列有要求,必须是有序表, 其实如果牵涉到有序表的搜索,都可以以二分查找为一个思路。
代码片段一,非递归方式:
var search = function(nums, target) {
if (!nums || nums.length === 0) return null
let left = 0, right = nums.length - 1;
// while (left < right) { 这里相等是一个边界条件
while (left <= right) {
let mid = Math.trunc((left + right) / 2)
let val = nums[mid]
if (target === val) {
return mid }
if (target < val) {
right = mid - 1
}
if (target > val) {
left = mid + 1
}
}
return -1
}
console.log(search([-1,0,3,5,9,12], 9))
代码片段二,递归方式:
// 递归方式
var search = function(nums, target, leftIndex, rightIndex ) {
if (!nums || nums.length === 0) {
return -1 }
let left = 0, right = (nums.length - 1);
if (leftIndex !== undefined) {
left = leftIndex }
if (rightIndex !== undefined) {
right = rightIndex }
let mid = Math.trunc((left + right) / 2)
let val = nums[mid]
// 边界条件
if (left > right) {
return -1 }
if (val === target) return mid
if (target > val) {
return search(nums, target, mid + 1, right)
}
if (target < val) {
return search(nums, target, left, mid - 1)
}
return -1
}
console.log(search([-1,0,3,5,9,12], 9))
平均查找长度计算:
对于二分查找来说,实际上有序表可以转换为一个特定的二叉树 称之为 【判定树】,比如有序表为 [-1, 0, 3, 5, 7, 9, 12], 转换成下面这颗二叉树,这颗二叉树有一些特点,每一层上面的节点,在查找成功的情况下,查找的次数为所在的层数(高度。)
5 第一层
/ \
0 9 第二层
/ \ / \
-1 3 7 12 第三层
假定表长为n,一共有n个节点。 表长为n = 2 ^ h - 1 , h=log2(n + 1)为树的高度。
优点 :查找效率比顺序查找高
缺点 : 必须是有序表,而且从存储结构来说只适用于顺序存储,不适用于链式存储。
3,分块查找
为什么有第三种分块查找,
因为顺序查找效率较低,二分查找虽然效率高,但是需要数据表为有序表,有序表就需要每一次插入删除数据的时候,会有大量的数据操作移动。
分块查找的概念是,将数据表分为多块, 每一块内内部的数据不要求排序。 但是每一块内的最大元素一定是小于下一块内的任意一个值。
主表数据(通过竖线分为3组,伪代码):
const rawList = [ 20, 15, 10, 8, 18, | 27, 22, 30, 24, 35, | 40, 46, 48, 60, 55 ] `
索引表:
const indexList = [
{
value: 20, index: 0, length: 5 } ,
{
value: 35, index: 5, length: 5 } ,
{
value: 60, index: 10, length: 5 }
]
比如我们现在要查找 27,先去索引表找到27属于那一块,然后在特定的一块中再去比较。
那么分块查找的平均查询长度为:
ASL = Lb + Lw
Lb为索引表的ASL,Lw为分块内的ASL。
假定 主表一共n个数据。每一块s条数据,那么就有n/s块。
块内的数据ASL为顺序查找 Lw = (s + 1) / 2
索引表的数据查询,这个分情况:
- 索引表如果是无序的线性表,那么
Lb = ( ( n / s) + 1 ) / 2 - 索引表如果是顺序存储的(有序)线性表,那么
Lb = log2( s + 1 ) - 1 - 索引表如果是散列表,那么
Lb = 1
那么ASL = Lw + Lb 是有3种情况。
优点 :查找效率适中,比顺序查找块,并且在块内的插入和删除无序移动大量的元素。
缺点 : 需要一个额外的索引表来存储各个块的信息。
总结
| 顺序查找 | 折半查找 | 分块查找 | |
|---|---|---|---|
| ASL | ( n + 1) / 2 | log2(n + 1) - 1 | 上面3种情况 |
| 表结构 | 有序表、无序表 | 有序表 | 分块有序(块内无要求) |
| 存储结构 | 顺序存储、链式存储 | 顺序存储 | 顺序存储、链式存储 |
参考资料:
王卓老师-分块查找
https://www.cnblogs.com/magic-sea/p/11391431.html
https://blog.csdn.net/jiary5201314/article/details/51125411