手撕BP网络，你值得拥有！

 

本文货很干，自己挑的文章，含着泪也要读完！

一、认识BP神经网络

       BP网络（Back-ProPagation Network）又称反向传播神经网络，分为两个过程：（1）工作信号正向传递子过程；（2）误差信号反向传递子过程。 通过样本数据的训练，不断修正网络权值和阈值使误差函数沿负梯度方向下降，逼近期望输出。它是一种应用较为广泛的神经网络模型，多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。

其实，BP神经网络就是一个“万能的模型+误差修正函数”，每次根据训练得到的结果与预想结果进行误差分析，进而修改权值和阈值，一步步得到输出和与预想结果一致的模型。举个例子：比如我们给客户开发出一个软件产品，根据客户的反馈，开发者对产品进一步升级和优化，从而交付出让用户更满意的产品，这就是BP神经网络的核心。

下面就让我们看看BP网络到底是什么东西？

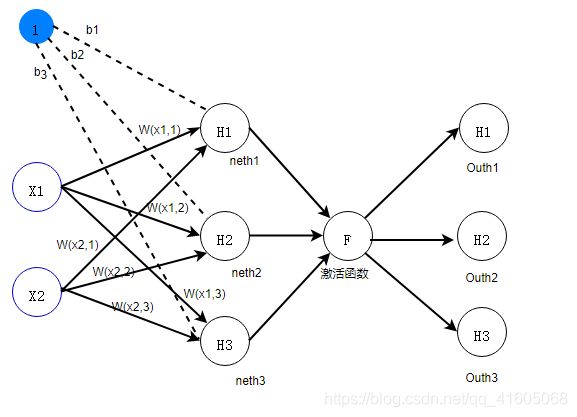
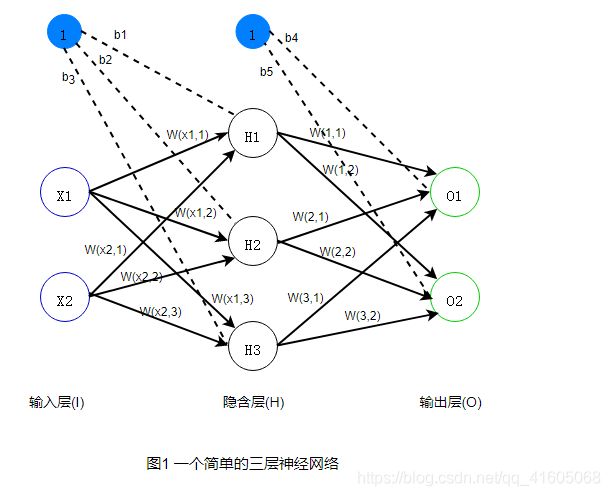
在BP神经网络中，单个样本有个输入，有个输出，在输入层和输出层之间通常还有若干个隐含层。实际上，1989年Robert Hecht-Nielsen证明了对于任何闭区间内的一个连续函数都可以用一个隐含层的BP网络来逼近，这就是万能逼近定理。所以一个三层的BP网络就可以完成任意的维到维的映射。即这三层分别是输入层（I），隐含层（H），输出层（O），隐含层的个数+输出层的个数=神经网络层数，也就是说神经网络的层数不包括输入层。如下图示：

二、神经网络结构

2.1神经元模型

2.2神经网络中的神经元

神经网络中的神经元就是为了模拟上述过程，典型的神经元模型如下：

三、BP算法的推导

图1所示是一个简单的三层（一个输入层、一个隐含层、一个输出层）神经网络结构。

 : 表示a神经元与b神经元的权重

: 表示第n个神经元的偏差

 3.1前向传播计算

3.1.1网络参数

输入数据：

激活函数：

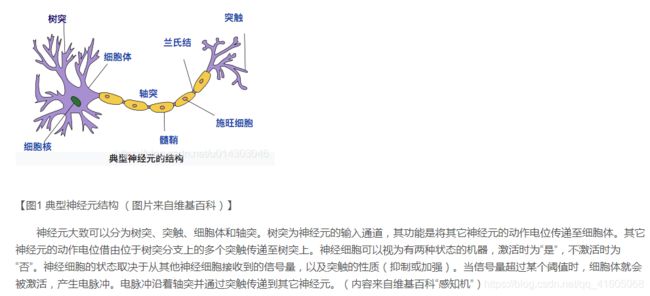
第一层网络参数：

第二层网络参数：

3.1.2隐含层公式推导

如图所示，隐含层有三个神经元：、、，

该层的输入为：,

即：

矩阵运算传送门：https://blog.csdn.net/qq_41605068/article/details/117449252

以神经元为例：

其输入为：

同理有：, 

假设选择作为该层的激活函数（同一层的激活函数都是一样的，不同层可以选择不同的激活函数），那么该层的输出为： ,  ,

3.1.3输出层公式推导

如图所示，输出层有两个神经元： ,  ，该层的输入为：

以神经元为例：

其输入为：

同理有：

假设选择作为该层的激活函数（同一层的激活函数都是一样的，不同层可以选择不同的激活函数），那么该层的输出为： ,   

3.2反向传播计算

• 反向传播推导
• 一文彻底搞懂BP算法
• AI从入门到放弃

3.2.0前提

1.损失函数和代价函数

损失函数主要指的是对于单个样本的损失或误差；

代价函数表示多样本同时输入模型的时候总体的误差——每个样本误差的和然后取平均值。

在BP神经网络中，误差信号反向传递子过程比较复杂，它是基于Widrow-Hoff学习规则的，假设输出层的所有结果为,使用误差函数如下：

，其中taeget为期望输出，output为实际输出。

而BP神经网络的主要目的是反复修正权值和阈值，使得误差函数达到最小，Widrow-Hoff学习规则是通过沿着相对误差平方和的最快下降方向，连续调整网络的权值和阈值，从而减少系统实际输出和期望输出的误差，这个规则也叫纠错学习规则。

2.梯度下降法原理

梯度矩阵（向量）求出来的意义是什么？从几何意义讲，梯度矩阵代表了函数增加最快的方向，因此，沿着与之相反的方向就可以更快找到最小值。如图所示：

梯度的输出变量表明了在每个位置损失函数增长最快的方向，它可表示为在函数的每个位置向哪个方向移动，函数值可以增长，梯度就是表明损失函数相对参数的变化率，对梯度进行缩放的参数就是学习率 

 如图，曲线对应于损失函数，点表示权值，梯度用箭头表示，表明了如果向右移动，就会增加损失，函数值就会增加多少，如果向反方向移动，损失就会减少。

反向传播的过程就是利用梯度下降法原理，慢慢的找到代价函数的最小值，从而得到最终的模型参数。

3.2.1输出层->隐含层【公式推导】

以w5为例：

如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则：传送门）

• 计算：因为只会接受,所以对求导为：
• 计算：

因为激活函数为：

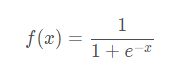，即求激活函数的导数（通过复合函数求导:传送门）：    ，此时，将该结果进行变形：

所以：

• 计算：

，对 求导：

【结论】所以： 三者相乘，得：

为了表达方便，我们用表示输出层误差：

所以：

  ,若为负，则

【权值更新】：

  (其中，为学习速率)

【偏差更新】

(其中，为学习速率)

3.2.2隐含层->输入层【公式推导】

以W1为例：

计算公式：,因为 会同时接受和，所以该公式中的，求解过程如上所示。

四、模型建立

4.1输入输出层设计

根据需求自行设定。

4.2权值初始化

4.2.1权重初始化的重要性

• 神经网络的训练过程中的参数学习时基于梯度下降算法进行优化的。梯度下降法需要在开始训练时给每个参数赋予一个初始值。这个初始值的选取十分重要。在神经网络的训练中如果将权重全部初始化为0，则第一遍前向传播过程中，所有隐藏层神经元的激活函数值都相同，导致深层神经元可有可无，这一现象称为对称权重现象。
• 为了打破这个平衡，比较好的方法是对每层的权重都进行随机初始化，这样使得不同层的神经元之间有很好的区分性。但是，随机初始化参数的一个问题是如何选择随机初始化的区间。如果权重初始化太小，会导致神经元的输入过小，随着层数的不断增加，会出现信号消失的问题；也会导致sigmoid激活函数丢失非线性的能力，因为在0附件sigmoid函数近似是线性的。如果参数初始化太大，会导致输入状态太大。对sigmoid激活函数来说，激活函数的值会变得饱和，从而出现梯度消失的问题。

4.2.2常用的参数初始化方法

• 高斯分布初始化：参数从一个固定均值(比如0)和固定方差(比如0.01)的高斯分布进行随机初始化。
• 均匀分布初始化：在一个给定的区间[-r,r]内采用均匀分布来初始化参数。超参数r的设置可以按照神经元的连接数量进行自适应的调整。
• 初始化一个深层神经网络时，一个比较好的初始化策略是保持每个神经元输入和输出的方差一致。

4.3隐含层设计

原理：有一个隐层的神经网络, 只要隐节点足够多, 就可以以任意精度逼近一个非线性函数。

注意：在网络设计过程中, 隐层神经元数的确定十分重要。隐层神经元个数过多, 会加大网络计算量并容易产生过度拟合问题; 神经元个数过少, 则会影响网络性能, 达不到预期效果。网络中隐层神经元的数目与实际问题的复杂程度、输入和输出层的神经元数以及对期望误差的设定有着直接的联系。目前, 对于隐层中神经元数目的确定并没有明确的公式, 只有一些经验公式, 神经元个数的最终确定还是需要根据经验和多次实验来确定。

本文在选取隐层神经元个数的问题上参照了以下的经验公式:

(n为输入层神经元个数, m 为输出层神经元个数, a 为[ 1, 10]之间的常数。)

4.4激活函数的选取

BP神经网络通常采用Sigmoid可微函数和线性函数作为网络的激励函数。本文选择S型正切函数tansig作为隐层神经元的激励函数。如果网络的输出归一到[ -1, 1]范围内, 因此预测模型选取S 型对数函数tansig作为输出层神经元的激励函数。

激活函数: 就是在神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

激活函数的作用： 激活函数对于深度学习来说非常的重要，我们假设现在有n个神经元x1，...，xn，其参数为w1，...，wn，偏值为b。

其中f为激活函数。我们可以发现如果没有激活函数的话，那么神经网络就变成了线性函数的不断嵌套，对于非线性关系学习不好。

激活函数需要的性质：

1. 连续可导的非线性函数，这样可以拟合非线性关系还可以用数值优化求解。
2. 激活函数及其导数其形式必须简单，这样加快网络的学习。
3. 激活函数的导数不能太大或者太小，最好稳定在1左右。太大会梯度爆炸，太小会梯度消失。   

       如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层输出都是上层输入的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了。 正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络就有意义了（不再是输入的线性组合，可以逼近任意函数）。最早的想法是sigmoid函数或者tanh函数，输出有界，很容易充当下一层输入（以及一些人的生物解释balabala）。

常见的激活函数包括：

• Sigmoid
• TanHyperbolic(tanh)
• ReLu
• softplus
• softmax
• ELU
• PReLU

比如Sigmoid：

常用的Sigmoid型函数有两种，第一个是logistic函数，第二个是tanh函数。这两个函数都是连续可导的，并且导数都不大，所以性质比较好，但是缺点在于他们都是两端饱和的，导数趋近于0。

1. 单极性logistic函数

       定义：

             

      导数为：

                 

      函数曲线如下图所示：

         

logistic函数是一个挤压函数，将实数域的输入转换为 ( 0 , 1 ) (0,1) (0,1)区间内的输出。当输入值接近0的时候，其趋近于线性函数，当输入之接近两侧无穷的时候，它是饱和的（导数为0）。

logistic函数的输出可以认定是一个概率分布；其可以看作是一个软性门来控制神经元输入的信息数量。

2.双极性Tanh函数

定义：

 tanh函数也是一个挤压函数，将实数域的输入转换到 ( − 1 , 1 ) (-1,1) (−1,1)区间内。它的输出是零均值的，所以在梯度下降法的应用中，Tanh函数的收敛速度更快。

4.5损失函数的选取

• 参考1

泛化性：表示BP神经网络在训练过程中，如果均方误差（MSE）连续6次不降反升，则网络停止训练。

误差精度： 关于mu参数含义的一种理解是，mu是误差精度参数，用于给神经网络的权重再加一个调制，这样可以避免在BP网络训练的过程中陷入局部最小值，mu的范围为0到1，即偏差。

PS: 这里我要说的是，用这个作为误差的计算，因为它简单，实际上用的时候效果不咋滴。如果激活函数是饱和的，带来的缺陷就是系统迭代更新变慢，系统收敛就慢，当然这是可以有办法弥补的，一种方法是使用交叉熵函数作为损失函数。

交叉熵做为代价函数能达到上面说的优化系统收敛下欧工，是因为它在计算误差对输入的梯度时，抵消掉了激活函数的导数项，从而避免了因为激活函数的“饱和性”给系统带来的负面影响。如果项了解更详细的证明可以点 --> 传送门

4.6设计原则

• 激活函数：

        

（可参考：https://blog.csdn.net/qq_41605068/article/details/118102576）

• 学习率：0<η<1
• 停止准则：网络的均方误差足够小或者训练足够的次数等
• 初始权值：以均值等于0的均匀分布随机挑选突触权值
• 隐层结构：

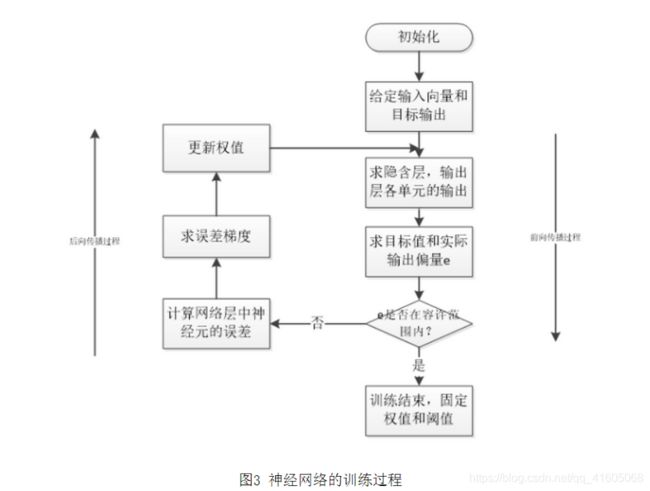
• 训练过程：如图3

     1.初始化网络的突触权值和阈值矩阵；

     2.训练样本的呈现；

     3.前向传播计算；

     4.误差反向传播计算并更新权值；

     5.迭代，用新的样本进行步骤3和4，直至满族停止准则；

• 参考1
• 参考2
• 参考3

五、后续

关于超参数：

通过前面的介绍，相信读者可以发现BP神经网络模型有一些参数是需要设计者给出的，也有一些参数是模型自己求解的。

  那么，哪些参数是需要模型设计者确定的呢？

  比如，学习率 α \alpha α，隐含层的层数，每个隐含层的神经元个数，激活函数的选取，损失函数（代价函数）的选取等等，这些参数被称之为超参数。

       其它的参数，比如权重矩阵 w w w和偏置系数 b b b在确定了超参数之后是可以通过模型的计算来得到的，这些参数称之为普通参数，简称参数。

       超参数的确定其实是很困难的。因为你很难知道什么样的超参数会让模型表现得更好。比如，学习率太小可能造成模型收敛速度过慢，学习率太大又可能造成模型不收敛；再比如，损失函数的设计，如果损失函数设计不好的话，可能会造成模型无法收敛；再比如，层数过多的时候，如何设计网络结构以避免梯度消失和梯度爆炸……

  神经网络的程序比一般程序的调试难度大得多，因为它并不会显式报错，它只是无法得到你期望的结果，作为新手也很难确定到底哪里出了问题（对于自己设计的网络，这种现象尤甚，我目前也基本是新手，所以这些问题也在困扰着我）。

当然，使用别人训练好的模型来微调看起来是一个捷径……

BP神经网络的注意点：

BP神经网络一般用于分类或者逼近问题。如果用于分类，则激活函数一般选用Sigmoid函数或者硬极限函数，如果用于函数逼近，则输出层节点用线性函数，即。BP神经网络在训练数据时可以采用增量学习或者批量学习。

增量学习要求输入模式要有足够的随机性，对输入模式的噪声比较敏感，即对于剧烈变化的输入模式，训练效果比较差，适合在线处理。

批量学习不存在输入模式次序问题，稳定性好，但是只适合离线处理。

标准BP神经网络的缺陷：

（1）容易形成局部极小值而得不到全局最优值。 BP神经网络中极小值比较多，所以很容易陷入局部极小值，这就要求对初始权值和阀值有要求，要使得初始权值和阀值随机性足够好，可以多次随机来实现。

（2）训练次数多使得学习效率低，收敛速度慢。

（3）隐含层的选取缺乏理论的指导。

（4）训练时学习新样本有遗忘旧样本的趋势。

BP算法的改进：

（1）增加动量项：引入动量项是为了加速算法收敛，即如下公式   ，动量因子一般选取。

（2）自适应调节学习率。

（3）引入陡度因子：通常BP神经网络在训练之前会对数据归一化处理，即将数据映射到更小的区间内，比如[0,1]或[-1,1]。