LSTM详解
LSTM详解
文章目录
- LSTM详解
-
- 改进
-
- 记忆单元
- 门控机制
- LSTM结构
- LSTM的计算过程
-
- 遗忘门
- 输入门
- 更新记忆单元
- 输出门
- LSTM单元的pytorch实现
- Pytorch中的LSTM
-
- 参数
- 输入
- 输出
- 参考与摘录
LSTM是RNN的一种变种,可以有效地解决RNN的梯度爆炸或者消失问题。关于RNN可以参考作者的另一篇文章https://blog.csdn.net/qq_40922271/article/details/120965322
LSTM的改进在于增加了新的记忆单元与门控机制
改进
记忆单元
LSTM进入了一个新的记忆单元 c t c_t ct,用于进行线性的循环信息传递,同时输出信息给隐藏层的外部状态 h t h_t ht。在每个时刻 t t t, c t c_t ct记录了到当前时刻为止的历史信息。
门控机制
LSTM引入门控机制来控制信息传递的路径,类似于数字电路中的门,0即关闭,1即开启。
LSTM中的三个门为遗忘门 f t f_t ft,输入门 i t i_t it和输出门 o t o_t ot
- f t f_t ft控制上一个时刻的记忆单元 c t − 1 c_{t-1} ct−1需要遗忘多少信息
- i t i_t it控制当前时刻的候选状态 c ~ t \tilde{c}_t c~t有多少信息需要存储
- o t o_t ot控制当前时刻的记忆单元 c t c_t ct有多少信息需要输出给外部状态 h t h_t ht
下面我们就看看改进的新内容在LSTM的结构中是如何体现的。
LSTM结构
如图一所示为LSTM的结构,LSTM网络由一个个的LSTM单元连接而成。
图二描述了图一中各种元素的图标,从左到右分别为,神经网络( σ 表 示 s i g m o i d \sigma表示sigmoid σ表示sigmoid)、向量元素操作( × \times ×表示向量元素乘, + + +表示向量加),向量传输的方向、向量连接、向量复制
LSTM 的关键就是记忆单元,水平线在图上方贯穿运行。
记忆单元类似于传送带。直接在整个链上运行,只有一些少量的线性交互。信息在上面流传保持不变会很容易。
LSTM的计算过程
遗忘门

在这一步中,遗忘门读取 h t − 1 h_{t-1} ht−1和 x t x_t xt,经由sigmoid,输入一个在0到1之间数值给每个在记忆单元 c t − 1 c_{t-1} ct−1中的数字,1表示完全保留,0表示完全舍弃。
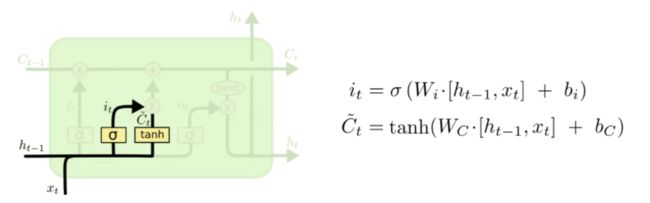
输入门
输入门将确定什么样的信息内存放在记忆单元中,这里包含两个部分。
- sigmoid层同样输出[0,1]的数值,决定候选状态 c ~ t \tilde{c}_t c~t有多少信息需要存储
- tanh层会创建候选状态 c ~ t \tilde{c}_t c~t
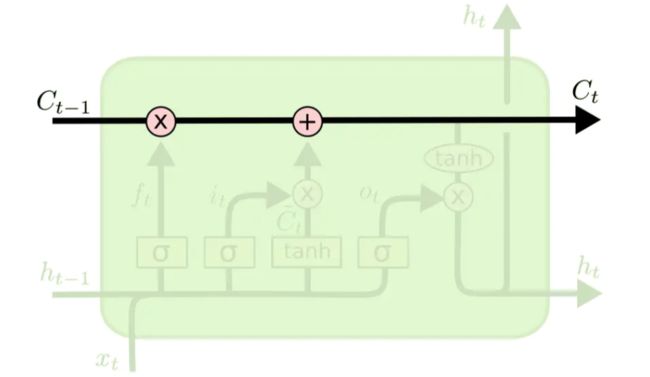
更新记忆单元
随后更新旧的细胞状态,将 c t − 1 c_{t-1} ct−1更新为 c t c_t ct
首先将旧状态 c t − 1 c_{t-1} ct−1与 f t f_t ft相乘,遗忘掉由 f t f_t ft所确定的需要遗忘的信息,然后加上 i t ∗ c ~ t i_t*\tilde{c}_t it∗c~t,由此得到了新的记忆单元 c t c_t ct
输出门
结合输出门 o t o_t ot将内部状态的信息传递给外部状态 h t h_t ht。同样传递给外部状态的信息也是个过滤后的信息,首先sigmoid层确定记忆单元的那些信息被传递出去,然后,把细胞状态通过 tanh层 进行处理(得到[-1,1]的值)并将它和输出门的输出相乘,最终外部状态仅仅会得到输出门确定输出的那部分。
通过LSTM循环单元,整个网络可以建立较长距离的时序依赖关系,以上公式可以简洁地描述为
[ c ~ t o t i t f t ] = [ t a n h σ σ σ ] ( W [ x t h t − 1 ] + b ) \begin{bmatrix} \tilde{c}_t \\ o_t \\ i_t \\ f_t \end{bmatrix} = \begin{bmatrix} tanh \\ \sigma \\ \sigma \\ \sigma \end{bmatrix} \begin{pmatrix} W \begin{bmatrix} x_t \\ h_{t-1} \end{bmatrix} +b \end{pmatrix} ⎣⎢⎢⎡c~totitft⎦⎥⎥⎤=⎣⎢⎢⎡tanhσσσ⎦⎥⎥⎤(W[xtht−1]+b)
c t = f t ⊙ c t − 1 + i t ⊙ c ~ t c_t=f_t \odot c_{t-1}+i_t \odot \tilde{c}_t ct=ft⊙ct−1+it⊙c~t
h t = o t ⊙ t a n h ( c t ) h_t=o_t \odot tanh(c_t) ht=ot⊙tanh(ct)
LSTM单元的pytorch实现
下面通过手写LSTM单元加深对LSTM网络的理解
class LSTMCell(nn.Module):
def __init__(self, input_size, hidden_size, cell_size, output_size):
super().__init__()
self.hidden_size = hidden_size # 隐含状态h的大小,也即LSTM单元隐含层神经元数量
self.cell_size = cell_size # 记忆单元c的大小
# 门
self.gate = nn.Linear(input_size+hidden_size, cell_size)
self.output = nn.Linear(hidden_size, output_size)
self.sigmoid = nn.Sigmoid()
self.tanh = nn.Tanh()
self.softmax = nn.LogSoftmax(dim=1)
def forward(self, input, hidden, cell):
# 连接输入x与h
combined = torch.cat((input, hidden), 1)
# 遗忘门
f_gate = self.sigmoid(self.gate(combined))
# 输入门
i_gate = self.sigmoid(self.gate(combined))
z_state = self.tanh(self.gate(combined))
# 输出门
o_gate = self.sigmoid(self.gate(combined))
# 更新记忆单元
cell = torch.add(torch.mul(cell, f_gate), torch.mul(z_state, i_gate))
# 更新隐藏状态h
hidden = torch.mul(self.tanh(cell), o_gate)
output = self.output(hidden)
output = self.softmax(output)
return output, hidden, cell
def initHidden(self):
return torch.zeros(1, self.hidden_size)
def initCell(self):
return torch.zeros(1, self.cell_size)
Pytorch中的LSTM
CLASS torch.nn.LSTM(*args, **kwargs)
参数
- input_size – 输入特征维数
- hidden_size – 隐含状态 h h h的维数
- num_layers – RNN层的个数:(在竖直方向堆叠的多个相同个数单元的层数),默认为1
- bias – 隐层状态是否带bias,默认为true
- batch_first – 是否输入输出的第一维为batchsize
- dropout – 是否在除最后一个RNN层外的RNN层后面加dropout层
- bidirectional –是否是双向RNN,默认为false
- proj_size – If
> 0, will use LSTM with projections of corresponding size. Default: 0
其中比较重要的参数就是hidden_size与num_layers,hidden_size所代表的就是LSTM单元中神经元的个数。从知乎截来的一张图,通过下面这张图我们可以看出num_layers所代表的含义,就是depth的堆叠,也就是有几层的隐含层。可以看到output是最后一层layer的hidden输出的组合
输入
input, (h_0, c_0)
- input: (seq_len, batch, input_size) 时间步数或序列长度,batch数,输入特征维度。如果设置了batch_first,则batch为第一维
- h_0: shape(num_layers * num_directions, batch, hidden_size) containing the initial hidden state for each element in the batch. Defaults to zeros if (h_0, c_0) is not provided.
- c_0: **shape(num_layers * num_directions, batch, hidden_size)**containing the initial cell state for each element in the batch. Defaults to zeros if (h_0, c_0) is not provided.
输出
output, (h_n, c_n)
- output: (seq_len, batch, hidden_size * num_directions) 包含每一个时刻的输出特征,如果设置了batch_first,则batch为第一维
- h_n: shape(num_layers * num_directions, batch, hidden_size) containing the final hidden state for each element in the batch.
- c_n: shape (num_layers * num_directions, batch, hidden_size) containing the final cell state for each element in the batch.
h与c维度中的num_direction,如果是单向循环网络,则num_directions=1,双向则num_directions=2
参考与摘录
https://blog.csdn.net/qq_40728805/article/details/103959254
https://zhuanlan.zhihu.com/p/79064602
https://www.jianshu.com/p/9dc9f41f0b29