深度学习-循环神经网络TensorFlow

循环神经网络结构

下图是一个典型的循环神经网络。循环神经网络的主体结构A的输入除了来自输入层xt，还有一个循环的边来提供上一时刻的隐藏状态ht−1。在每一时刻，循环神经网络的模块A在读取了xt和ht−1之后会生成新的隐藏状态ht，并产生本时刻的输出ot。循环神经网络当前的状态ht是根据上一时刻的状态ht−1和当前的输入xt共同决定的。

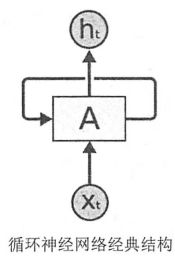
在时刻t，状态ht浓缩了前面序列x0,x1,…,xt−1的信息，用于作为输出ot的参考。由于序列长度可以无限长，维度有限的h状态不可能将序列的全部信息都保存下来，因此模型必须学习只保留与后面任务ot,ot+1,…相关的最重要的信息。
循环神经网络对长度为N的序列展开后，可以视为一个有N个中间层的前馈神经网络。这个前馈神经网络没有循环链接，因此可以直接使用反向传播算法进行训练，而不需要任何特别的优化算法。这样的训练方法称为“沿时间反向传播”，是训练循环神经网络最常见的方法。

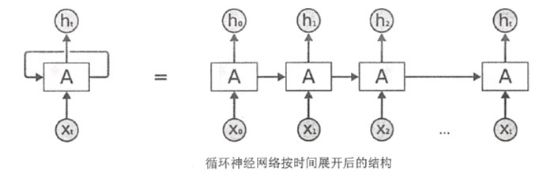
从循环神经网络的结构特征很容易看出它最擅长解决与时间序列相关的问题。对于一个序列数据，可以将这个序列上不同时刻的数据依次传入循环神经网络的输入层，而输出可以是对序列下一时刻的预测，也可以是对当前时刻信息的处理结果（如语音识别结果）。循环神经网络要求每一个时刻都有一个输入，但是不一定每个时刻都需要有输出。在过去几年中，循环神经网络被广泛地应用在语音识别、语言模型及时序分析等问题上，并取得了巨大的成功。

循环神经网络可以看作是同一神经网络结构在时间序列上被复制多次的结果，这个被复制多次的结构被称为循环体。下图展示了一个最简单的循环体结构。

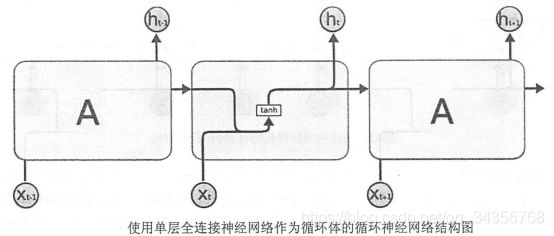
循环神经网络中的状态是通过一个向量来表示的，这个向量的维度也称为循环神经网络隐藏层的大小，假设其为n。 假设输入向量的维度为x，隐藏层状态的维度为n，那么图中循环体的全连接层神经网络的输入大小为x+n。也就是将上一时刻的状态与当前时刻的输入拼接成一个大的向量作为循环体中神经网络的输入。因为该全连接层的输出为当前时刻的状态，于是输出层的节点个数也为n，循环体中的参数个数为(n+x)*n+n个。

循环体状态与最终输出的维度通常不同，因此为了将当前时刻的状态转化为最终的输出，循环神经网络还需要另外一个全连接神经网络类完成这个过程。这和卷积神经网络中最后的全连接层的意义是一样的。 在得到循环神经网络的前向传播结果之后，可以和其他神经网络类似地定义损失函数。循环神经网络唯一的区别在于因为它每个时刻都有一个输出，所以循环神经网络的总损失为所有时刻（或部分时刻）上的损失函数的总和。

理论上循环神经网络可以支持任意长度的序列，然而在实际训练过程中，如果序列过长，一方面会导致训练时出现梯度消失和梯度爆炸的问题；另一方面，展开后的循环神经网络会占用过大的内存，所以实际中会规定一个最大长度，当序列长度超过规定长度后会对序列进行截断。

长短时记忆网络（LSTM）结构

当前预测位置和相关信息之间的文本间隔不断增大时，简单循环神经网络有可能会丧失学习到距离过远的信息的能力，或者在复杂语言场景中，有用信息的间隔有大有小、长短不一，循环神经网络的性能也会受到限制。

长短时记忆模型（long short-term memory，LSTM）的设计就是为了解决这个问题。采用LSTM结构的循环神经网络比标准的循环神经网络表现更好。与单一tanh循环体结构不同，LSTM是一种拥有三个“门”结构的特殊网络结构。

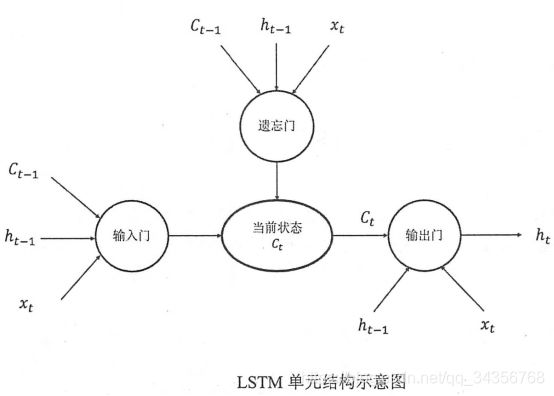
LSTM靠一些“门”的结构让信息有选择性地影响循环神经网络中每个时刻的状态。所谓“门”结构就是一个使用sigmoid神经网络和一个按位做乘法的操作，这两个操作合在一起就是一个“门”的结构。使用sigmoid作为激活函数的全连接神经网络层会输出一个0到1之间的数值，描述当前输入有多少信息量可以通过这个结构。当门打开时（sigmoid神经网络层输出为1时），全部信息都可以通过；当门关上时（sigmoid神经网络层输出为0时），任何信息都无法通过。

上图中“遗忘门”和“输入门”可以使神经网更有效的保存长期记忆。“遗忘门”的作用是让循环神经网络忘记之前没有用的信息。“遗忘门”会根据当前输入xt和上一时刻输出ht−1决定哪一部分记忆需要被遗忘。

（1）假设状态c的维度为n。“遗忘门”会根据当前输入xt和上一时刻输出ht−1计算一个维度为n的向量f=sigmoid(W1x+W2h)，它的每一维度上的值都在（0,1）范围内，再将上一时刻的状态ct−1与f向量按位相乘，那么f取值接近0的维度上的信息就会被“忘记”，而f取值接近1的维度上的信息会被保留。比如先介绍了某地原来是绿水蓝天，后来被污染了。于是在看到被污染之后，循环神经网络应该“忘记”之前绿水蓝天的状态。

（2）在循环网络“忘记”了部分之前的状态后，它还需要从当前的输入补充最新的记忆。这个过程由“输入门”完成。“输入门”会根据xt和ht−1决定哪些信息加入到状态ct−1中生成新的状态ct。
比如当看到环境被污染之后，模型需要将这个信息写入新的状态。

（3）LSTM结构在计算得到新的状态ct后需要产生当前时刻的输出，这个过程由“输出门”完成。“输出门”会根据最新的状态ct、上一时刻的输出ht−1和当前的输入xt来决定该时刻的输出ht。

比如当前的状态为被污染，那么“天空的颜色”后面的单词很有可能是“灰色的”。
具体LSTM每个“门”的公式定义如下：
z=tanh(Wz[ht−1,xt]) 输入值
i=sigmoid(Wi[ht−1,xt]) 输入门
f=sigmoid(Wf[ht−1,xt]) 遗忘门
o=sigmoid(Wo[ht−1,xt]) 输出门
ct=fct−1+iz 新状态
ht=o⋅tanhct 输出
其中Wz,W_i,Wf,W_o,是4个维度为[2n,n]的参数矩阵。

TensorFlow实现LSTM

通过TensorFlow可以很方便地实现LSTM结构的循环神经网络，并不需要对LSTM内部结构有很深入的了解。

# 定义一个LSTM结构。在Tensorflow中通过一句简单的命令就可以实现一个完整的LSTM结构
# LSTM中使用的变量也会在该函数中自动被声明

lstm=tf.nn.rnn.cell.BasicLSTMCell(lstm_hidden_size)

# 将LSTM中的状态初始化为全0数组。BasicLSTMCell类提供了zero_state函数来生成全0初始状态。state是一个包含两个张量的LSTMStateTuple类，其中state.c和state.h分别对应了上述c状态和h状态。和其他神经网络类似，在优化循环神经网络时，每次也会使用一个batch的训练样本，在以下代码中，batch_size给出了一个batch的大小。
state=lstm.zero_state(batch_size,tf.float32)

# 定义损失函数
loss=0.0

# 虽然在测试时循环神经网络可以处理任意长度的序列，但是在训练中为了将循环神经网络展开成前馈神经网络，需要知道训练数据的序列长度。在以下代码中，用num_steps来表示这个长度。后面会介绍使用dynamic_rnn动态处理变长序列的方法。
for i in range(num_steps):
    # 在第一时刻声明LSTM结构中使用的变量，在之后的时刻都需要复用之前定义好的变量。
    if i>0:
        tf.get_variable_scpoe.reuse_variables()
    # 每一步处理时间序列中的一个时刻。将当前输入current_input和前一时刻状态state(h_t-1和c_t-1)传入定义
    # 的LSTM结构可以得到当前LSTM的输出lstm_output(ht)和更新后状态state(ht和ct)。lstm_output用于输出
    # 给其他层，state用于输出给下一时刻，他们在dropout等方面可以有不同的处理方式。
    lstm_output,state=lstm(current_input,state)
    # 将当前时刻LSTM结构的输出传入一个全连接层得到最后的输出
    final_output=fully_connected(lstm_output)
    # 计算当前时刻输出的损失
    loss+=calc_loss(final_output,expected_output)
# 使用常规神经网络的方法训练模型

双向循环神经网络

在经典的循环神经网络中，状态和传输是从前往后单向的。然而在有些问题中，当前时刻的输出不仅和之前的状态有关，也和之后的状态相关。这时需要使用双向循环神经网络（bidirectional RNN）来解决这个问题。双向循环神经网络是由两个独立的循环神经网络叠加在一起组成的。输出由这两个循环神经网络的输出拼接而成。下图展示了一个双向循环神经网络的结构：

在每一个时刻t，输入会同时提供给这两个方向相反的循环神经网络、两个独立的网络独立进行计算，各自产生该时刻的新状态和输出，而双向循环神经网络的最终输出是这两个单向循环神经网络的输出的简单拼接。两个循环神经网络除方向不同以外，其余结构完全对称。每一个网络中的循环体可以自由选用任意结构，RNN或LSTM。

TensorFlow实现BiLSTM

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author  : Laochen

from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
import numpy as np

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data",one_hot=True)

#参数
learning_rate = 0.001

# 可以理解为，训练时总共用的样本数
training_iters = 100000

# 每次训练的样本大小
batch_size = 128

# 这个是用来显示的。
display_step = 10

# 网络参数
# n_steps*n_input其实就是那张图 把每一行拆到每个time step上。
n_input = 28 # MNIST data input (img shape: 28*28)
n_steps = 28 # timesteps

# 隐藏层大小
n_hidden = 128 #隐藏层的功能数量
n_classes = 10 # MNIST 

x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes])

weights = {
     
    'out': tf.Variable(tf.random_normal([2*n_hidden, n_classes]))}
biases = {
     
    'out': tf.Variable(tf.random_normal([n_classes]))}

def BiRNN(x, weights, biases):

    #准备数据形状以匹配`bidirectional_rnn`功能要求
    #当前数据输入形状：（batch_size，n_steps，n_input）
    #所需形状：'n_steps'张量形状列表（batch_size，n_input）
    #取消堆栈以获取形状的'n_steps'张量列表（batch_size，n_input）
    # 变成了n_steps*(batch_size, n_input)
    x = tf.unstack(x, n_steps, 1)

    #使用tensorflow定义lstm单元格
    # 前向方向单元
    lstm_fw_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)
    #向后方向的单元
    lstm_bw_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)

    # 获取lstm单元格输出
    try:
        outputs, _, _ = rnn.static_bidirectional_rnn(lstm_fw_cell,    
lstm_bw_cell, x,dtype=tf.float32)
    except Exception: 
        outputs = rnn.static_bidirectional_rnn(lstm_fw_cell,   
lstm_bw_cell, x,dtype=tf.float32)

    # 线性激活，使用rnn内环最后输出
    return tf.matmul(outputs[-1], weights['out']) + biases['out']

pred = BiRNN(x, weights, biases)

#定义损失和优化器
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, 
labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

# 评估模型
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

#初始化变量
init = tf.global_variables_initializer()

# 启动图
with tf.Session() as sess:
    sess.run(init)
    step = 1
    #继续训练，直到达到最大迭代次数
    while step * batch_size < training_iters:
        batch_x, batch_y = mnist.train.next_batch(batch_size)
        # 重塑数据
        batch_x = batch_x.reshape((batch_size, n_steps, n_input))
        # 运行优化op（backprop）
        sess.run(optimizer, feed_dict={
     x: batch_x, y: batch_y})
        if step % display_step == 0:
            # 计算批次准确性
            acc = sess.run(accuracy, feed_dict={
     x: batch_x, y: batch_y})
            # 计算批量损失
            loss = sess.run(cost, feed_dict={
     x: batch_x, y: batch_y})
            print("Iter " + str(step*batch_size) + 
", Minibatch Loss=" + \
                  "{:.6f}".format(loss) + ", Training Accuracy= " + \
                  "{:.5f}".format(acc))
         step += 1
    print("Optimization Finished!")

    test_len = 128
    test_data = mnist.test.images[:test_len].reshape((-1, n_steps, 
n_input))
    test_label = mnist.test.labels[:test_len]
    
	print("Testing Accuracy:", \
        sess.run(accuracy, feed_dict={
     x: test_data, y: test_label}))

深层循环神经网络

深层循环神经网络（Deep RNN）是循环神经网络的另一种变种。为了增强模型的表达能力，可以在网络中设置多个循环层，将每层循环网络的输出传给下一层进行处理。下图展示了一个深层循环神经网络的结构：

在一个L层的深层循环网络中，每一时刻的输入xtxtx_t到输出ototo_t之间有L个循环体，网络因此可以从输入中抽取更加高层的信息。和卷积神经网络类似，每一层的循环体中参数是一致的，而不同层中的参数可以不同。

TensorFlow实现多层LSTM

Tensorflow中提供了MultiRNNCell类来实现深层循环神经网络的前向传播过程。只需要在BasicLSTMCell的基础上再封装一层MultiRNNCell就可以非常容易地实现深层循环神经网络了。

# 定义一个基本的LSTM结构作为循环体的基础结构。深层循环神经网络也支持使用其他的循环体结构
lstm_cell=tf.nn.rnn.cell.BasicLSTMCell
# 通过MUltiRNNCell类实现深层循环神经网络中每一个时刻的前向传播过程。其中number_of_layers表示有多少层，即从x_t到o_t需要经过多少个LSTM结构。

stacked_lstm=tf.nn.rnn_cell.MultiRNNCell([lstm_cell(lstm_size) for _ in range(number_of_layers)])

# 和经典的循环神经网络一样，可以通过zero_state函数来获取初始状态
state=stacked_lstm.zero_state(batch_size,tf.float32)

# 计算每一时刻的前向传播结果
for i in range(len(num_steps)):
    if i>0:
        tf.get_variable_scope().reuse_variables()
        stacked_lstm_output,state=stacked_lstm(current_input,state)
        final_output=fully_connected(stacked_lstm_output)
        loss+=calc_loss(final_output,expected_output)