keras实战-入门之回归模型

回归模型

因为比较简单，就不多说了，看代码吧，当入门学习吧。

import numpy as np

#设置随机因子，使得每次随机都是同样的结果，要不同结果就改因子
np.random.seed(11)

from keras.models import Sequential
from keras.layers import Dense

import matplotlib.pyplot as plt

#-1 到 1取间隔200个点
X=np.linspace(-1,1,200)
#混洗X，即打乱X的排列顺序
np.random.shuffle(X)
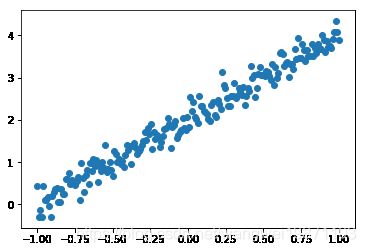
#定义Y=2X+2 加上正态分布均值0 标准差0.2 的噪音
Y=2*X+2+np.random.normal(0,0.2,(200,))

plt.scatter(X,Y)
plt.show()

#截取训练集和测试集 160训练 40测试
x_train=X[:160]
y_train=Y[:160]
x_test=X[160:]
y_test=Y[160:]

#单层的节点，1个输入，1个输出
model=Sequential()
model.add(Dense(units=1, input_dim=1))

#SGD为优化器，损失函数为均方误差
model.compile(optimizer='sgd',loss='mse')

#训练100轮，一次梯度下降16个数据，验证集占20%
model.fit(x_train,y_train,epochs=100,batch_size=16,verbose=2,validation_split=0.2)

Train on 128 samples, validate on 32 samples
Epoch 1/100
 - 0s - loss: 4.3086 - val_loss: 3.0746
Epoch 2/100
 - 0s - loss: 3.2675 - val_loss: 2.3085
Epoch 3/100
 - 0s - loss: 2.4983 - val_loss: 1.7496
Epoch 4/100
 - 0s - loss: 1.9315 - val_loss: 1.3411
Epoch 5/100
 - 0s - loss: 1.5081 - val_loss: 1.0410
Epoch 6/100
 - 0s - loss: 1.1892 - val_loss: 0.8194
Epoch 7/100
 - 0s - loss: 0.9512 - val_loss: 0.6544
Epoch 8/100
 - 0s - loss: 0.7696 - val_loss: 0.5312
Epoch 9/100
 - 0s - loss: 0.6316 - val_loss: 0.4377
Epoch 10/100
 - 0s - loss: 0.5248 - val_loss: 0.3663
Epoch 11/100
 - 0s - loss: 0.4413 - val_loss: 0.3110
Epoch 12/100
 - 0s - loss: 0.3763 - val_loss: 0.2679
Epoch 13/100
 - 0s - loss: 0.3239 - val_loss: 0.2335
Epoch 14/100
 - 0s - loss: 0.2820 - val_loss: 0.2057
Epoch 15/100
 - 0s - loss: 0.2480 - val_loss: 0.1830
Epoch 16/100
 - 0s - loss: 0.2198 - val_loss: 0.1641
Epoch 17/100
 - 0s - loss: 0.1966 - val_loss: 0.1483
Epoch 18/100
 - 0s - loss: 0.1771 - val_loss: 0.1348
Epoch 19/100
 - 0s - loss: 0.1606 - val_loss: 0.1233
Epoch 20/100
 - 0s - loss: 0.1466 - val_loss: 0.1132
Epoch 21/100
 - 0s - loss: 0.1345 - val_loss: 0.1045
Epoch 22/100
 - 0s - loss: 0.1241 - val_loss: 0.0968
Epoch 23/100
 - 0s - loss: 0.1150 - val_loss: 0.0900
Epoch 24/100
 - 0s - loss: 0.1071 - val_loss: 0.0839
Epoch 25/100
 - 0s - loss: 0.1001 - val_loss: 0.0785
Epoch 26/100
 - 0s - loss: 0.0940 - val_loss: 0.0737
Epoch 27/100
 - 0s - loss: 0.0887 - val_loss: 0.0694
Epoch 28/100
 - 0s - loss: 0.0840 - val_loss: 0.0655
Epoch 29/100
 - 0s - loss: 0.0797 - val_loss: 0.0620
Epoch 30/100
 - 0s - loss: 0.0760 - val_loss: 0.0589
Epoch 31/100
 - 0s - loss: 0.0727 - val_loss: 0.0561
Epoch 32/100
 - 0s - loss: 0.0698 - val_loss: 0.0536
Epoch 33/100
 - 0s - loss: 0.0672 - val_loss: 0.0514
Epoch 34/100
 - 0s - loss: 0.0649 - val_loss: 0.0494
Epoch 35/100
 - 0s - loss: 0.0628 - val_loss: 0.0475
Epoch 36/100
 - 0s - loss: 0.0609 - val_loss: 0.0459
Epoch 37/100
 - 0s - loss: 0.0593 - val_loss: 0.0444
Epoch 38/100
 - 0s - loss: 0.0578 - val_loss: 0.0431
Epoch 39/100
 - 0s - loss: 0.0566 - val_loss: 0.0419
Epoch 40/100
 - 0s - loss: 0.0554 - val_loss: 0.0408
Epoch 41/100
 - 0s - loss: 0.0543 - val_loss: 0.0398
Epoch 42/100
 - 0s - loss: 0.0534 - val_loss: 0.0390
Epoch 43/100
 - 0s - loss: 0.0525 - val_loss: 0.0382
Epoch 44/100
 - 0s - loss: 0.0518 - val_loss: 0.0375
Epoch 45/100
 - 0s - loss: 0.0512 - val_loss: 0.0368
Epoch 46/100
 - 0s - loss: 0.0505 - val_loss: 0.0363
Epoch 47/100
 - 0s - loss: 0.0501 - val_loss: 0.0358
Epoch 48/100
 - 0s - loss: 0.0496 - val_loss: 0.0353
Epoch 49/100
 - 0s - loss: 0.0492 - val_loss: 0.0349
Epoch 50/100
 - 0s - loss: 0.0488 - val_loss: 0.0345
Epoch 51/100
 - 0s - loss: 0.0484 - val_loss: 0.0342
Epoch 52/100
 - 0s - loss: 0.0482 - val_loss: 0.0339
Epoch 53/100
 - 0s - loss: 0.0479 - val_loss: 0.0336
Epoch 54/100
 - 0s - loss: 0.0476 - val_loss: 0.0333
Epoch 55/100
 - 0s - loss: 0.0474 - val_loss: 0.0331
Epoch 56/100
 - 0s - loss: 0.0472 - val_loss: 0.0329
Epoch 57/100
 - 0s - loss: 0.0470 - val_loss: 0.0327
Epoch 58/100
 - 0s - loss: 0.0469 - val_loss: 0.0326
Epoch 59/100
 - 0s - loss: 0.0468 - val_loss: 0.0324
Epoch 60/100
 - 0s - loss: 0.0467 - val_loss: 0.0323
Epoch 61/100
 - 0s - loss: 0.0465 - val_loss: 0.0322
Epoch 62/100
 - 0s - loss: 0.0464 - val_loss: 0.0321
Epoch 63/100
 - 0s - loss: 0.0464 - val_loss: 0.0319
Epoch 64/100
 - 0s - loss: 0.0463 - val_loss: 0.0319
Epoch 65/100
 - 0s - loss: 0.0462 - val_loss: 0.0318
Epoch 66/100
 - 0s - loss: 0.0462 - val_loss: 0.0317
Epoch 67/100
 - 0s - loss: 0.0461 - val_loss: 0.0316
Epoch 68/100
 - 0s - loss: 0.0461 - val_loss: 0.0316
Epoch 69/100
 - 0s - loss: 0.0460 - val_loss: 0.0315
Epoch 70/100
 - 0s - loss: 0.0460 - val_loss: 0.0314
Epoch 71/100
 - 0s - loss: 0.0459 - val_loss: 0.0314
Epoch 72/100
 - 0s - loss: 0.0460 - val_loss: 0.0314
Epoch 73/100
 - 0s - loss: 0.0459 - val_loss: 0.0313
Epoch 74/100
 - 0s - loss: 0.0459 - val_loss: 0.0313
Epoch 75/100
 - 0s - loss: 0.0459 - val_loss: 0.0312
Epoch 76/100
 - 0s - loss: 0.0458 - val_loss: 0.0312
Epoch 77/100
 - 0s - loss: 0.0458 - val_loss: 0.0312
Epoch 78/100
 - 0s - loss: 0.0458 - val_loss: 0.0312
Epoch 79/100
 - 0s - loss: 0.0458 - val_loss: 0.0311
Epoch 80/100
 - 0s - loss: 0.0458 - val_loss: 0.0311
Epoch 81/100
 - 0s - loss: 0.0458 - val_loss: 0.0311
Epoch 82/100
 - 0s - loss: 0.0457 - val_loss: 0.0311
Epoch 83/100
 - 0s - loss: 0.0457 - val_loss: 0.0311
Epoch 84/100
 - 0s - loss: 0.0458 - val_loss: 0.0311
Epoch 85/100
 - 0s - loss: 0.0457 - val_loss: 0.0311
Epoch 86/100
 - 0s - loss: 0.0458 - val_loss: 0.0310
Epoch 87/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 88/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 89/100
 - 0s - loss: 0.0458 - val_loss: 0.0310
Epoch 90/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 91/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 92/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 93/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 94/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 95/100
 - 0s - loss: 0.0457 - val_loss: 0.0310
Epoch 96/100
 - 0s - loss: 0.0457 - val_loss: 0.0309
Epoch 97/100
 - 0s - loss: 0.0457 - val_loss: 0.0309
Epoch 98/100
 - 0s - loss: 0.0457 - val_loss: 0.0309
Epoch 99/100
 - 0s - loss: 0.0457 - val_loss: 0.0309
Epoch 100/100
 - 0s - loss: 0.0457 - val_loss: 0.0309

#输出权重
w,b=model.layers[0].get_weights()
print(w,b)

[[1.9986827]] [2.0133998]

#评估测试集损失
cost=model.evaluate(x_test,y_test)

40/40 [==============================] - 0s 238us/step

print(cost)

0.04056257084012031

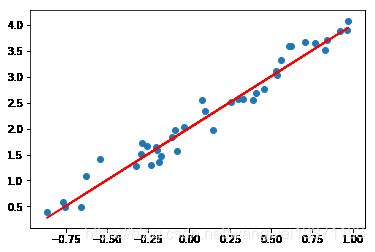
#预测测试集的Y，并可视化
y_pre=model.predict(x_test)
plt.scatter(x_test,y_test)
plt.plot(x_test,y_pre,'r')
plt.show()

好了，今天就到这里了，希望对学习理解有帮助，大神看见勿喷，仅为自己的学习理解，能力有限，请多包涵，侵删。