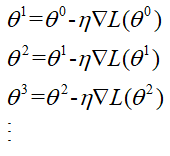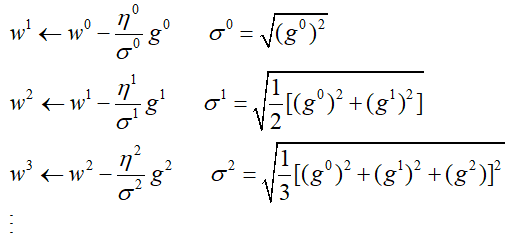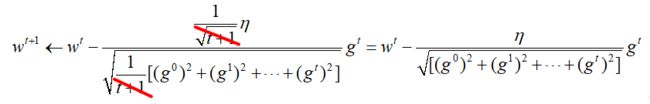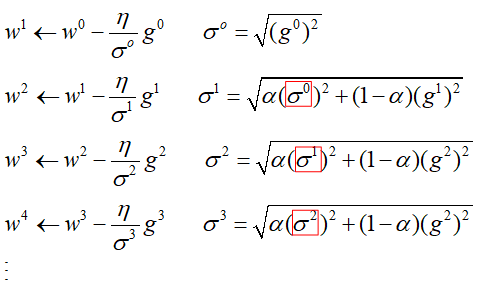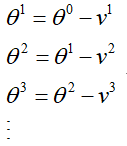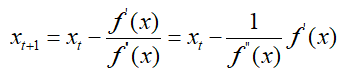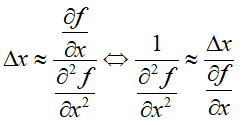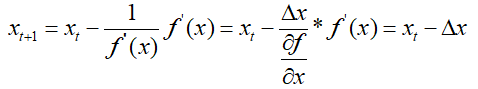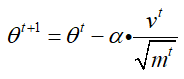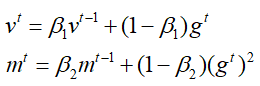【机器学习基础】——梯度下降

梯度下降是机器学习中一种重要的优化算法，不单单涉及到经典机器学习算法，在神经网络、深度学习以及涉及到模型参数训练的很多场景都要用到梯度下降算法，因此在此单独作为1节对这部分进行总结，主要从梯度下降的原理，优化的梯度下降方法包括SGD、MBGD、Adagrad、Momentm、RMSprop、Adam等算法，并依据可视化比较各算法的性能，资料主要来源于视频、论文和博客，参考资料会在末尾贴出。

---

梯度下降原理

常规梯度下降

　　前面提到梯度下降算法就是损失函数Loss梯度方向的反方向前进，即Loss等高线的发现方向前进，不断寻找使得Loss减小的参数，直至损失收敛，不再减小。我们用Θ表示参数，用▽L表示Loss的梯度，那么参数的更新就是：

　　假设Θ是2维的，有两个参数Θ1和Θ2，那么在二维空间中，参数的更新过程如图所示：

　　上图中红色的线是梯度的方向，参数朝着梯度的反方向移动，上述就是参数更新的过程，每次更新我们计算所有样本的损失对参数的导数的和（因为损失是一个加和公式），然后更新参数，这里就会有个问题，当我们样本量巨大时，我们每更新迭代一次，都要去对所有样本都计算以便，这样就会造成速度非常慢，因此在此基础上产生了随机梯度下降算法(SGD)和小批量（批量）梯度下降算法(MBGD)。

所谓随机梯度下降算法，就是在训练过程中仅选取一个样本即损失函数相当于从L变成了L'：

　　然后计算梯度，计算梯度，更新参数，随机梯度下降虽然提升了运行速度，但是也存在一定的缺点：

　　（1）每次仅选取一个样本，会造成损失的严重震荡，即有时大有时小，其收敛性和原始梯度下降是一样的，但有时也可能会跳到更优的局部最小值。

　　而小批量梯度下降类似于随机梯度下降，不过是每次从仅选取一个样本变成将样本分成多个batch，每次采用一小批样本对参数进行更新。小批量梯度下降与原始梯度下降一样也会受到学习率的影响，后面即将说到，当到达鞍点时，会在鞍点附近来回震荡。

　　从原始梯度下降的图中可以看出，每次移动的长度由梯度和学习率共同决定，这里就有个重要的参数——学习率η，那么这里就有个问题，到底每次移动多长合适呢，下面有张图来说明：

　　图中黑色的曲线表示Loss的曲线，有①、②、③、④四个不同大小的学习率，学习率其中②是学习率最小，①次之，③学习率稍大，④学习率最大，那么从图中我们可以看到，②的步长很小，每次前进一小步，而③则是一次性跨过鸿沟，错过了Local Minma，而④则步长过大，甚至朝着损失增大的方向移动了，只有②是最理想的前进步伐，因此设定合适的学习率不但可以使得优化次数减小，同时可以获得更好的优化效果。

　　那么如何调整学习率呢？从上面的图来看，红色的线是理想的梯度下降的前进方向和步伐，我们期望在梯度比较大的地方，即比较陡峭的地方，下降的快一点，步伐快一点，而在比较平缓的地方，希望步伐小一点，那么我们如何做到在训练过程中自动调整学习率的大小呢？于是就衍生出了自动调整学习率的梯度下降算法Adagrad、Momentum、RMSprop、Adam等算法，其中除了Momentum、RMSprop、Adam主要在深度学习中用的比较多，由于这些都属于梯度下降，且都是动态调整学习率，再次一并说了。

Adagrad

　　Adagrad中的Ada全称Adaptive Learning Rates，是一种动态调整学习率的过程，其主旨思想是：在刚开始训练阶段，我们离目标还比较远，可以步伐大一点，当训练几次后，我们更接近目标值，此时我们要减小学习的步伐。每次乘上一个1/√t+1，那么在第t次训练时学习率就变成了：

　　这时随着训练次数变大，学习率逐渐减小，而Adagrad更进一步地在每次训练时会再除以过去所有的梯度的均方误差（RMS），用σ^t表示，设当前一轮迭代的梯度为g^t，那么参数的更新即为：

 　　结合上面每次学习率每次衰减1/√t+1，进一步化简上式，那么最终的参数更新公式为：

　　这样会在梯度平缓的地方，学习的更加缓慢，更加平稳，从而取得更大的进步。

RMSprop

　　但是Adagrad也会有缺点，当学习到一定程度时，分母项变得越来越大，最终导致学习率为0，参数不再更新。为了改善这个问题，就出现了RMSprop算法，RMSprop不再是将过去的梯度直接求平方和，而是通过给予过去梯度都赋予一定的权重，然后再求平方和，相当于是逐渐遗忘过去的梯度，将新的梯度信息更加的突出出来，也就是“移动平均”的做法。用数学的描述RMSprop的参数更新过程如下：

 Momentum

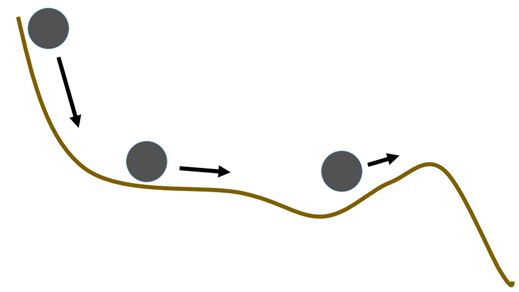
　　另一种类似于RMSprop算的优化算法就是Momentum，其在梯度下降过程中不仅考虑了梯度的方向，同时运用了物理学中动量的原理，在下降过程中考虑了动量的因素，想象一辆过山车，在比较陡峭的地方下降的快，动量大，在平缓的地方就速度小，动量小，如下图所示：

　　那么将其运用在梯度下降的过程中就是这样的：

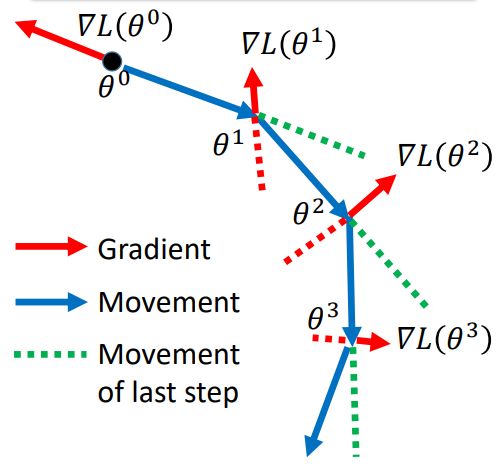
　　上面的图中红色是梯度的方向，蓝色的线是动量方向，从θ⁰开始，梯度方向与动量进行合成，合成以后形成绿色的虚线，到达新的点后，重复以上步骤（这个图有时间将其制作成动图可能看的更清楚）。那么在每次前进中，动量用v表示，那么动量的变化过程如下：

　　那么参数 Θ的更新过程就是考虑了动量，其更新过成为：

　　仔细观察动量变化的公式，将t之前的动量带到t的动量公式中，即：

　　可以看到动量其实就是之前的梯度乘以一个权重λ在加和的结果，至此可以看出Momentum算法其实跟RMSprop其实很像，不过RMSprop是加权的平方和。

　　上面的算法都是需要给定初始化学习率η，那么还有一种是不需要给出初始学习率类似于Adagrad的算法Adadelta。

Adadelta

　　通过牛顿法知道，利用牛顿迭代公式求最小值，牛顿法的迭代步长为f(x)^'',那么：

　　可以看出参数的迭代的步长至于f(x)的二阶导数有关，不需要指定学习率。而高阶的牛顿法迭代步长为Hessian矩阵，因此Adadelta就是采用了这种思想，采用Hessian矩阵的对角线近似Hessian矩阵，于是：

 　　那么：

　　假设x附近的曲率是平滑的，xt+1近似为xt，那么：

　　 这一部分暂时理解不是很透彻，后面会搜索一些资料，暂时先放这里吧。

Adam

　　Adam算法是刚好整合上面两种RMSprop和Monentum的方法，因此其全程为自适应时刻估计方法（Adaptive Moment Estimation），其实就是带有动量的RMSprop算法。既然是结合RMSprop和Momentum，我们首先给出参数更新公式：

　　其中v是关于动量的变量，m是过去梯度的加权的平方和，与RMSprop类似，二者的更新过程如下：

　　由于训练初始化v和m为0，则会导致vt和mt也偏向于0，尤其是在训练初期，为了防止偏差对训练初期的影响，需要对vt和mt进行修正：

　　修正完成后，即可带入上面参数更新的公式即可。

　　然后就是还有一些其他的优化算法，如NAG、Adamax、Nadam等比较新的方法，这里就暂时不作介绍了。

　　接下来就是对上面一些算法的实现，每一个算法会用一个小实例看一下算法的迭代过程，算法代码仅作为学习算法加深印象，不考虑算法的性能和速度。

算法的实现

常规梯度下降

　　这个比较简单，就简单对其做一个实现，然后顺便验证一下前面的线性回归算法，首先就是写一个梯度下降的函数：

import numpy as np
import matplotlib.pyplot as plt

def gd(x, y, w, b):
    m, n = np.shape(x)
    hypo = 2 * (y.reshape(m) - (np.dot(w, x.T) + b))
    grad_w = -np.dot(hypo, x)/m
    grad_b = -np.sum(hypo)/m
    loss = np.sum((hypo/2) ** 2)/m
    return grad_w, grad_b, loss

　　这样一个简单的梯度下降就完成了，先创建一些简单的数据，对梯度下降算法进行验证：

# f(x1, x2) = 3x + 1
x = [[0], [1], [3], [2.2], [9], [6], [4], [4.5], [5.5], [7.7]]
def f(x):
    z = []
    for x_ in x:
        z.append(3 * x_[0] + 1)
    return z

y = f(x)

data_x = np.array(x)
labels = np.array(y)

m, n = np.shape(data_x)

　　然后就可以利用梯度下降对算法进行训练了：

w = np.array([0] * n)
b = 0

eta = 0.0001
w_list = []
b_list = []
loss_list = []
for i in range(0, 10000):
　　 w_list.append(w)
　　 b_list.append(b)
    grad_w, grad_b, loss = gd(data_x, labels, w, b)
    w = w - eta * grad_w
    b = b - eta * grad_b
    loss_list.append(loss)

　　然后画图看下参数的更新过程：

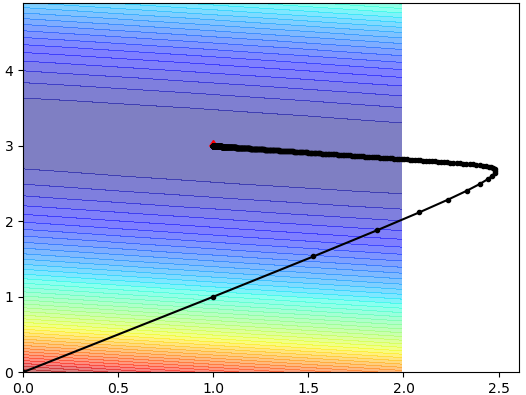
W = np.arange(0, 5, 0.1)
B = np.arange(0, 2, 0.01)
Z = np.zeros((len(W), len(B)))
for i in range(len(W)):
    for j in range(len(B)):
        w = W[i]
        b = B[j]
        Z[i][j] = 0
        for k in range(len(data_x)):
            Z[i][j] += (y[k] - w * data_x[k][0] - b) ** 2
        Z[i][j] /= len(data_x)


plt.figure()
plt.contourf(B, W, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))
plt.plot([1], [3.], 'x', ms=6, marker=10, color='r')

plt.plot(b_list, w_list, 'o-', ms=3, lw=1.5, color='black')

　　背景颜色深浅表示loss的大小，红色的点是标准方程的参数（3,1），黑色线就是参数逐渐向目标值靠近的过程，最终得到一组参数（w=3.0003，b=0.998）。

　　然后用sklearn自带的数据集跑一下上面的过程，首先读入数据，在重复上面的过程：

from sklearn.datasets import load_boston

data_x = load_boston()['data']
labels = load_boston()['target']

m, n = np.shape(data_x)

w = np.array([0] * n)
b = 0
eta = 0.0001
w_list = []
b_list = []
loss_list = []
for i in range(0, 10000):
    grad_w, grad_b, loss = gd(data_x, labels, w, b)
    w = w - eta * grad_w
    w_list.append(w)
    b = b - eta * grad_b
    b_list.append(b)
    loss_list.append(loss)

　　最终loss收敛在57左右，前面提到学习率大小的问题，刚开始设置0.001的学习率时，loss范围越来越大，最终发散了，大概就是上面那个图中④中的线的样子，查找原因发现在写gd函数时没有除以样本数，这也就间接导致了学习率变大，因此后面减小学习率后结果才会收敛。

 SGD

　　每次迭代仅选取一个样本对参数进行更新，添加一个随机选取的索引就可以了：

def sgd(x, y, w, b):
    idx = random.randint(0, len(x)-1)
    select_x = x[idx]
    select_y = y[idx]
    hypo = 2 * (select_y - (np.dot(w, select_x) + b))
    grad_w = -np.dot(hypo, select_x)
    grad_b = -hypo
    loss = (np.sum((y.reshape(m) - (np.dot(w, x.T) + b)) ** 2))/len(x)
    return grad_w, grad_b, loss

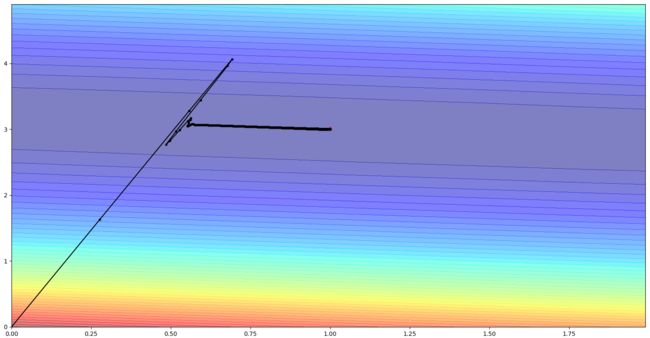
　　替换掉上面迭代的函数“gd”为“sgd”，看一下迭代过程：

　　对比一下上面那个过程，可以看出前面的迭代过程对比全量数据梯度下降还是有点曲折的，只不过这里数据量比较少，不是那么明显。最终学习到的参数基本与全量梯度下降一致。

Adagrad

　　Adagrad要叠加过去所有梯度的和的平方再开根号，代码如下：

def adagrad(x, y, w, b, grad_w_list, grad_b_list):

    grad_w, grad_b, loss = gd(x, y, w, b)

    if len(grad_w_list) == 0:
        sum_grad_w = 0
        sum_grad_b = 0
    else:
        sum_grad_w = 0
        sum_grad_b = 0
        for i in range(len(grad_w_list)):
            sum_grad_w += grad_w_list[i] ** 2
            sum_grad_b += grad_b_list[i] ** 2

    sum_grad_w = sum_grad_w + grad_w**2
    sum_grad_b = sum_grad_b + grad_b**2
    delta_w = grad_w/np.sqrt(sum_grad_w)
    delta_b = grad_b/np.sqrt(sum_grad_b)
    return delta_w, delta_b, grad_w, grad_b, loss

　　然后就是训练：

w = np.array([0] * n)
b = 0
eta = 1
w_list = []
grad_w_list = []
b_list = []
grad_b_list = []
loss_list = []
for i in range(0, 10000):
　　 w_list.append(w)
    b_list.append(b)
    delta_w, delta_b, grad_w, grad_b, loss = adagrad(data_x, labels, w, b, grad_w_list, grad_b_list)
    w = w - eta * delta_w
    grad_w_list.append(grad_w)
    b = b - eta * delta_b
    grad_b_list.append(grad_b)
    loss_list.append(loss)
    print(i, loss)

　　刚开始设置的eta值很小，收敛极慢，当设置足够大时很快就收敛了，这也正是adagrad的特性：可以刚开始设置较大的学习率，随后随着迭代次数的增加，学习率自动调整。从图中可以看到一开始步长较大，直接飞出去了，随后又被拉了回来，从输出的loss可以看出，adagrad的效果还是不错的，最终找到的w、b值与真实值一致，学习效果比上面两个都要好。

Momentum

　　Momentum方法在下降过程中带有动量，可以帮助在优化过程中突破鞍点，同时可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛，下面是Momentum的实现：

def momentum(lamda, eta, w_v_list, b_v_list, grad_w_list, grad_b_list):
    if len(w_v_list) == 0:
        w_v = 0
        b_v = 0
    else:
        w_v = lamda * w_v_list[-1] + eta * grad_w_list[-1]
        b_v = lamda * b_v_list[-1] + eta * grad_b_list[-1]
    return w_v, b_v

# 训练

w = np.array([0] * n)
b = 0
eta = 0.01
lamda = 0.01
w_list = []
grad_w_list = []
b_list = []
grad_b_list = []
loss_list = []
w_v_list = []
b_v_list = []
for i in range(0, 10000):
    grad_w, grad_b, loss = gd(data_x, labels, w, b)
    w_v, b_v = momentum(lamda, eta, w_v_list, b_v_list, grad_w_list, grad_b_list)
    grad_w_list.append(grad_w)
    grad_b_list.append(grad_b)
    w = w - w_v
    b = b - b_v
    loss_list.append(loss)
    w_v_list.append(w_v)
    b_v_list.append(b_v)
    w_list.append(w)
    b_list.append(b)
    print(i, loss)

　　再看一下Momentum的优化过程：

　　该样本数据其实是不存在鞍点的，可以看到，开始时由于动量较大，稍微向外冲出去了，但随后由于梯度的存在，再次将方向拉了回来，最终收敛，收敛后的参数w、b与真实值一致，并且收敛速度很快。

RMSprop

　　RMSprop类似于Adagrad，不过在前面的梯度平方和进行了加权，下面是RMSprop的实现：

def rmsprop(x, y, w, b, sigma_w_list, sigma_b_list, alpha):
    grad_w, grad_b, loss = gd(x, y, w, b)
    if len(sigma_w_list) == 0:
        sigma_w = grad_w
        sigma_b = grad_b
    else:
        sigma_w = np.sqrt(alpha * sigma_w_list[-1] ** 2 + (1 - alpha) * grad_w ** 2)
        sigma_b = np.sqrt(alpha * sigma_b_list[-1] ** 2 + (1 - alpha) * grad_b ** 2)
    return sigma_w, sigma_b, grad_w, grad_b, loss

# 训练
w = np.array([0] * n)
b = 0
eta = 0.001
alpha = 0.9
w_list = []
sigma_w_list = []
b_list = []
sigma_b_list = []
loss_list = []
for i in range(0, 10000):
    sigma_w, sigma_b, grad_w, grad_b, loss = rmsprop(data_x, labels, w, b, sigma_w_list, sigma_b_list, alpha)
    w = w - eta * grad_w/sigma_w
    w_list.append(w)
    sigma_w_list.append(sigma_w)
    b = b - eta * grad_b/sigma_b
    b_list.append(b)
    sigma_b_list.append(sigma_b)
    loss_list.append(loss)
    print(i, loss)

　　得到的结果如图所示：

　　这个训练过程相较于Adagrad看着就比较“光滑”，训练到最后收敛结果满足要求。

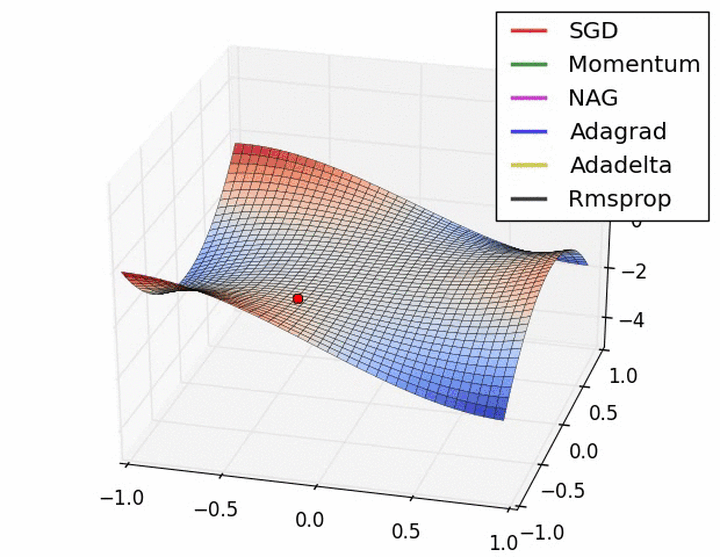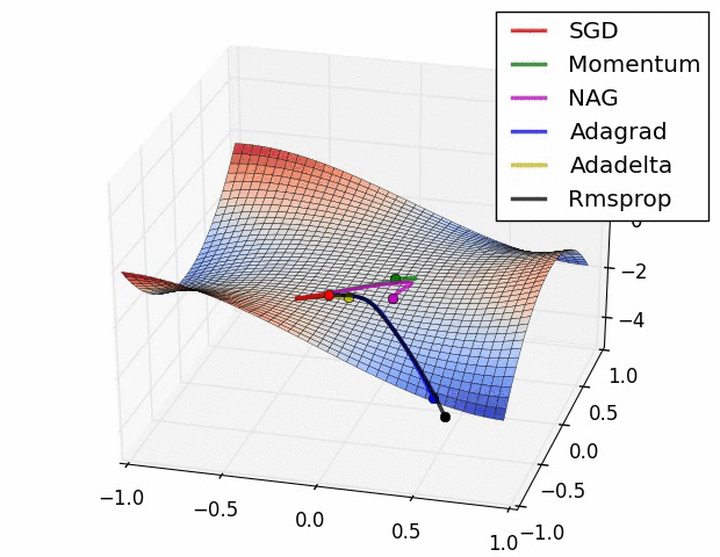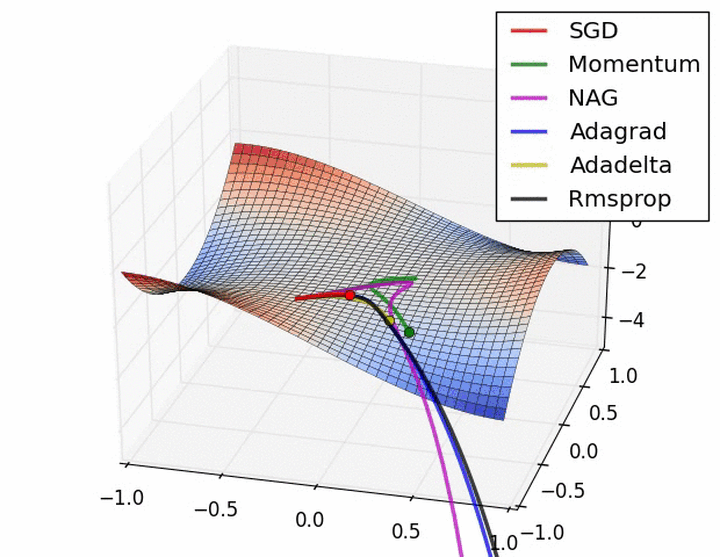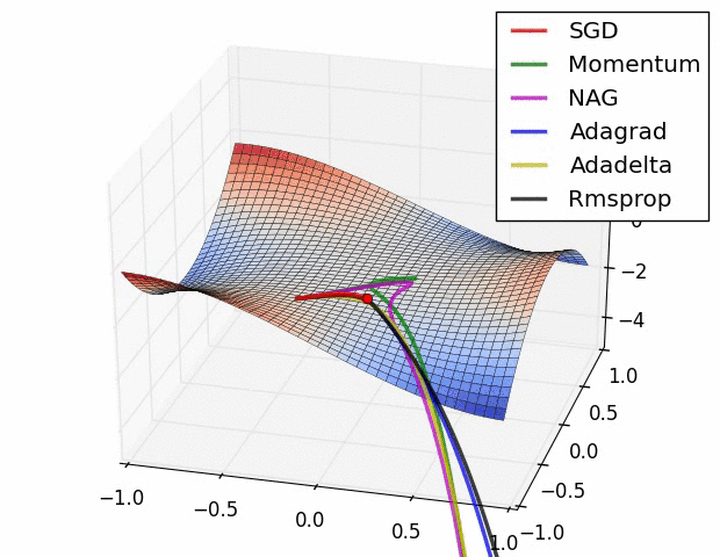
　　后面的梯度下降算法就不再进一步实现和叙述了，大多都是公式的编辑和实现，比较简单，其实在实现过程中w、b是可以作为一个参数进行学习和训练的，在此只是为了容易看的明白，因此分开来了，最后附上其他博客中的几种算法动态效果图，来更直观显示每一种算法的特点，一个是没有鞍点的和一个是有鞍点存在的情况：

梯度下降算法的选择

　　那么众多梯度下降算法在使用时应该选择哪一种呢，这要根据样本的特性来选择：

　　如果数据是稀疏的，或者对训练时间要求较高，就采用自适应调整学习率的方法，如Adagrad、RMSprop、Adadelta、Adam，而后面三者由于加入了加权平均，在效果上是相似的，随着梯度变得稀疏，Adam整体效果要比RMSprop好，如果不知道选用哪种方法，Adam是最好的选择。

　　在很多研究中经常用的SGD算法，SGD一般来说效果比较好，但相比其他算法时间可能较长，同时可能会被困在鞍点，但SGD依旧在论文中很受欢迎。

　　以上就是梯度下降部分内容了，其实还有一些其他的比较新的梯度下降算法，后面附上梯度下降overview文献，其实还有一些其他的优化算法，如最小二乘、牛顿法、拟牛顿法等，后面有时间会再进行学习。

 

参考资料：

梯度下降overview原文：https://arxiv.org/pdf/1609.04747.pdf

如何选择梯度下降算法文献：http://www.redcedartech.com/pdfs/Select_Optimization_Method.pdf

优化算法的可视化：http://louistiao.me/notes/visualizing-and-animating-optimization-algorithms-with-matplotlib/

梯度下降总结：https://www.cnblogs.com/guoyaohua/p/8542554.html

 

---

因为时间关系，最近比较忙，这一篇更新时间较长，而且因为梯度下降是一个比较重要的算法，所以就自己实现了一遍（但代码很烂），再涉及这方面内容就简单回顾一下不再叙述了，参考资料的文献还是有时间有必要再仔细研读一下。