机器学习 —— KNN算法简单入门
机器学习 —— KNN算法简单入门
- 第1关:手动实现简单kNN算法
-
- 1 KNN算法简介
-
- 1.1 kNN 算法的算法流程
- 1.2 kNN 算法的优缺点
- 1.3 编程要求+参数解释
- 2. 代码实现
- 3. 个人总结
-
- 3.1 numpy库的学习
-
- 3.1.1 NumPy Ndarray 对象
- 3.2 python基本语法
- 3.3 手写knn待改进
- 第2关:红酒分类
-
- 1. 基础知识
-
- 1.1 数据集介绍
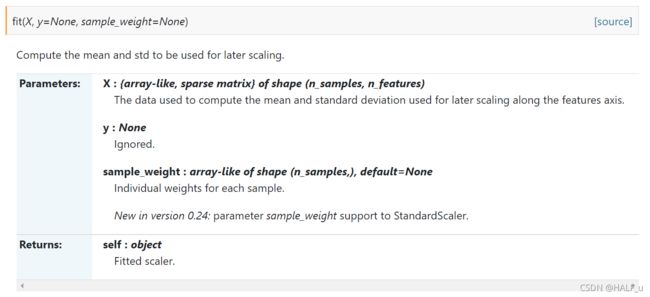
- 1.2 StandardScaler的使用
- 1.3 KNeighborsClassifier的使用
- 1.4 编程要求+测试说明
- 2. 代码实现
- 3. 总结
-
- 3.1 python使用
- 3.2 代码问题
- 3.3 调用方法简要分析
-
- 3.3.1 StandardScaler缩放了什么?
- 3.3.2 fit 和 fit_transform 和 transform
- 第3关:莫名其妙地把前两关拆分成六关来写……
-
- 1. KNN算法再学习
-
- 1.1 简介
- 1.2 kNN算法的优缺点
- 2. 使用sklearn中的kNN算法进行分类
-
- 2.1 更进一步了解K近邻算法
- 2.2 了解sklearn中KNeighborsClassifier的参数
- 2.3 编程要求+测试说明
- 2.4 实现代码
- 3. 使用sklearn中的kNN算法进行回归
-
- 3.1 在sklearn中使用KNeighborsRegressor
- 3.2 编程要求+测试说明
- 3.3 代码实现
- 4. 分析红酒数据
-
- 4.1 背景知识补充
- 4.2 编程要求+测试说明
- 4.3 代码实现
- 5. 对数据进行标准化
-
- 5.1 标准化相关知识
- 5.2 编程要求+测试说明
- 5.3 代码实现
- 6. 使用kNN算法进行预测
-
- 6.1 编程要求+测试说明
- 6.2 代码实现
第1关:手动实现简单kNN算法
1 KNN算法简介
1.1 kNN 算法的算法流程
kNN 算法其实是众多机器学习算法中最简单的一种,因为该算法的思想完全可以用 8 个字来概括:“近朱者赤,近墨者黑”。
假设现在有这样的一个样本空间,该样本空间里有宅男和文艺青年这两个类别,其中红圈表示宅男,绿圈表示文艺青年。如下图所示:

其实构建出这样的样本空间的过程就是 kNN 算法的训练过程。可想而知 kNN 算法是没有训练过程的,所以 kNN 算法属于懒惰学习算法。
假设我在这个样本空间中用黄圈表示,如下图所示:
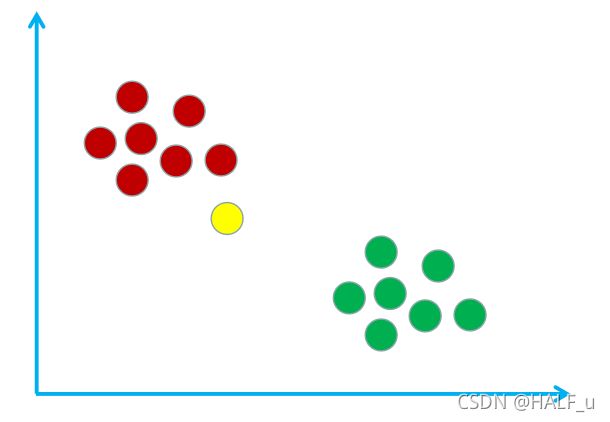
现在使用 kNN 算法来鉴别一下我是宅男还是文艺青年。首先需要计算我与样本空间中所有样本的距离。假设计算得到的距离表格如下:
| 样本编号 | 1 | 2 | … | 13 | 14 |
|---|---|---|---|---|---|
| 标签 | 宅男 | 宅男 | … | 文艺青年 | 文艺青年 |
| 距离 | 11.2 | 9.5 | … | 23.3 | 37.6 |
然后找出与我距离最小的 k 个样本(k 是一个超参数,需要自己设置,一般默认为 5),假设与我离得最近的 5 个样本的标签和距离如下:
| 样本编号 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| 标签 | 宅男 | 宅男 | 宅男 | 文艺青年 | 文艺青年 |
| 距离 | 11.2 | 9.5 | 7.7 | 5.8 | 15.2 |
最后只需要对这 5 个样本的标签进行统计,并将票数最多的标签作为预测结果即可。如上表中,宅男是 4 票,文艺青年是 1 票,所以我是宅男。
注意:有的时候可能会有票数一致的情况,比如 k=4 时与我离得最近的样本如下:
| 样本编号 | 4 | 9 | 11 | 13 |
|---|---|---|---|---|
| 标签 | 宅男 | 宅男 | 文艺青年 | 文艺青年 |
| 距离 | 4.2 | 9.5 | 7.7 | 5.8 |
可以看出宅男和文艺青年的比分是 2:2,那么可以尝试将属于宅男的 2 个样本与我的总距离和属于文艺青年的 2 个样本与我的总距离进行比较。然后选择总距离最小的标签作为预测结果。在这个例子中预测结果为文艺青年(宅男的总距离为 4.2+9.5,文艺青年的总距离为 7.7+5.8)。
1.2 kNN 算法的优缺点
从算法流程中可以看出,kNN 算法的优点有:
- 原理简单,实现简单;
- 天生支持多分类,不像其他二分类算法在进行多分类时要使用 OvO、 OvR 的策略。
缺点也很明显:
- 当数据量比较大或者数据的特征比较多时,预测过程的时间效率太低。
1.3 编程要求+参数解释
根据提示,在右侧编辑器的 begin-end 区域补充代码,完成 kNNClassifier 类中的 fit 函数与 predict 函数。
fit 函数用于 kNN 算法的训练过程,其中:
- feature :训练集数据,类型为 ndarray;
- label :训练集标签,类型为 ndarray。
predict 函数用于实现 kNN 算法的预测过程,函数返回预测的标签,其中:
- feature :测试集数据,类型为 ndarray。(PS:feature中有多条数据)
只需完成 fit 与 predict 函数即可,程序内部会调用您所完成的 fit 函数构建模型并调用 predict 函数来对数据进行预测。预测的准确率高于 0.9 视为过关。
2. 代码实现
# encoding=utf8
import numpy as np
class kNNClassifier(object):
def __init__(self, k):
'''
初始化函数
:param k:kNN算法中的k
'''
self.k = k
# 用来存放训练数据,类型为ndarray
self.train_feature = None
# 用来存放训练标签,类型为ndarray
self.train_label = None
def fit(self, feature, label):
'''
kNN算法的训练过程
:param feature: 训练集数据,类型为ndarray
:param label: 训练集标签,类型为ndarray
:return: 无返回
'''
# ********* Begin *********#
# self.train_feature = np.array(feature)
# self.train_label = np.array(label)
self.train_feature = np.array(feature)
self.train_label = np.array(label)
# ********* End *********#
def predict(self, feature):
'''
kNN算法的预测过程
:param feature: 测试集数据,类型为ndarray
:return: 预测结果,类型为ndarray或list
'''
'''
def _predict(test_data):
distances = [np.sqrt(np.sum((test_data - vec) ** 2)) for vec in self.train_feature]
nearest = np.argsort(distances)
topK = [self.train_label[i] for i in nearest[:self.k]]
votes = {}
result = None
max_count = 0
for label in topK:
if label in votes.keys():
votes[label] += 1
if votes[label] > max_count:
max_count = votes[label]
result = label
else:
votes[label] = 1
if votes[label] > max_count:
max_count = votes[label]
result = label
return result
predict_result = [_predict(test_data) for test_data in feature]
return predict_result
'''
# ********* Begin *********#
def mypredict(test_data):
# 计算欧氏距离并按照增序排序
distances = []
for i in self.train_feature:
distances.append(np.sqrt(np.sum((test_data - i) ** 2)))
nearest = np.argsort(distances)
# 选取距离最近的k个实例
neighbors = []
for i in nearest[:self.k]:
neighbors.append(self.train_label[i])
# 获取距离最近的k个实例中占比例较大的分类
# 这个预测不够好,如果分类的可能票数一致,还需要根据最近k个的最近距离进行处理比较
classVotes = {
}
max_count = 0
result = None
for label in neighbors:
if label in classVotes.keys():
classVotes[label] += 1
if classVotes[label] > max_count:
max_count = classVotes[label]
result = label
else:
classVotes[label] = 1
if classVotes[label] > max_count:
max_count = classVotes[label]
result = label
# 返回预测结果
return result
# 预测过程
predict_result = []
for test_data in feature:
predict_result.append(mypredict(test_data))
# 返回预测结果
return predict_result
# ********* End *********#
3. 个人总结
3.1 numpy库的学习
英文好的看这个:官方文档
英文不好的看这儿:好人一生平安
但是第二个链接搜索做的一般……
还可以参考这个:菜鸟教程yyds
3.1.1 NumPy Ndarray 对象
NumPy 最重要的一个特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
ndarray 对象是用于存放同类型元素的多维数组。
ndarray 中的每个元素在内存中都有相同存储大小的区域。
ndarray 内部由以下内容组成:
- 一个指向数据(内存或内存映射文件中的一块数据)的指针。
- 数据类型或 dtype,描述在数组中的固定大小值的格子。
- 一个表示数组形状(shape)的元组,表示各维度大小的元组。
- 一个跨度元组(stride),其中的整数指的是为了前进到当前维度下一个元素需要"跨过"的字节数。
- 具体描述
3.2 python基本语法
记录一下犯蠢的时候……python的基础语法真的目前很不熟练
- for、if、while这类语法结束后不写冒号,要写要写要写!!!
- 好好缩进
- 字典 {} 和列表 [] 傻傻分不清楚……
- 待补充……
3.3 手写knn待改进
就是代码块中我说的缺点,基本思路就是按照1.1算法流程里提及的那样的第二种情况。
第2关:红酒分类
1. 基础知识
1.1 数据集介绍
数据集为一份红酒数据,总共有 178 个样本,每个样本有 13 个特征,这里不会为你提供红酒的标签,你需要自己根据这 13 个特征对红酒进行分类。部分数据如下图:

1.2 StandardScaler的使用
由于数据中有些特征的标准差比较大,例如 Proline 的标准差大约为 314。如果现在用 kNN 算法来对这样的数据进行分类的话, kNN 算法会认为最后一个特征比较重要。因为假设有两个样本的最后一个特征值分别为 1 和 100,那么这两个样本之间的距离可能就被这最后一个特征决定了。这样就很有可能会影响 kNN 算法的准确度。为了解决这种问题,我们可以对数据进行标准化。
标准化的手段有很多,而最为常用的就是 Z Score 标准化。Z Score 标准化通过删除平均值和缩放到单位方差来标准化特征,并将标准化的结果的均值变成 0 ,标准差为 1。
sklearn 中已经提供了 Z Score 标准化的接口 StandardScaler,使用代码如下:
from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
# 实例化StandardScaler对象
scaler = StandardScaler()
# 用data的均值和标准差来进行标准化,并将结果保存到after_scaler
after_scaler = scaler.fit_transform(data)
# 用刚刚的StandardScaler对象来进行归一化
after_scaler2 = scaler.transform([[2, 2]])
print(after_scaler)
print(after_scaler2)
打印结果如下:
[[-1. -1.]
[-1. -1.]
[ 1. 1.]
[ 1. 1.]]
[[3. 3.]]
根据打印结果可以看出,经过准换后,数据已经缩放成了均值为 0,标准差为1的分布。
1.3 KNeighborsClassifier的使用
想要使用 sklearn 中使用 kNN 算法进行分类,只需要如下的代码(其中 train_feature、train_label 和 test_feature 分别表示训练集数据、训练集标签和测试集数据):
from sklearn.neighbors import KNeighborsClassifier
#生成K近邻分类器
clf=KNeighborsClassifier()
#训练分类器
clf.fit(train_feature, train_label)
#进行预测
predict_result=clf.predict(test_feature)
但是当我们需要调整 kNN 算法的参数时,上面的代码就不能满足我的需求了。这里需要做的改变在clf=KNeighborsClassifier()这一行中。
KNeighborsClassifier() 的构造函数包含一些参数的设定。比较常用的参数有以下几个:
- n_neighbors :即 kNN 算法中的 K 值,为一整数,默认为 5;
- metric :距离函数。参数可以为字符串(预设好的距离函数)或者是callable对象。默认值为闵可夫斯基距离;
- p :当 metric 为闵可夫斯基距离公式时可用,为一整数,默认值为 2,也就是欧式距离。
1.4 编程要求+测试说明
根据提示,在右侧编辑器的 begin-end 间补充代码,完成 classification 函数。函数需要完成的功能是使用 KNeighborsClassifier 对 test_feature 进行分类。其中函数的参数如下:
- train_feature : 训练集数据,类型为 ndarray;
- train_label : 训练集标签,类型为 ndarray;
- test_feature : 测试集数据,类型为 ndarray。
平台会对你返回的预测结果来计算准确率,你只需完成 classification 函数即可。准确率高于 0.9 视为过关。
2. 代码实现
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
import numpy as np
def classification(train_feature, train_label, test_feature):
'''
对test_feature进行红酒分类
:param train_feature: 训练集数据,类型为ndarray
:param train_label: 训练集标签,类型为ndarray
:param test_feature: 测试集数据,类型为ndarray
:return: 测试集数据的分类结果
'''
# ********* Begin *********#
# # 实例化StandardScaler函数
# scaler = StandardScaler()
# train_feature = scaler.fit_transform(np.array(train_feature).reshape(133, 13))
# test_feature = scaler.transform(np.array(test_feature).reshape(45, 13))
# # 生成K近邻分类器
# clf = KNeighborsClassifier()
# # 训练分类器
# clf.fit(train_feature, train_label.astype('int'))
# # 进行预测
# predict_result = clf.predict(test_feature)
# return predict_result
# 实例化StandardScaler对象
scaler = StandardScaler()
# 用np.array(train_feature).reshape(133, 13)即前133条数据的均值和标准差来进行标准化
# 并将结果保存到train_feature
train_feature = scaler.fit_transform(np.array(train_feature).reshape(133, 13))
# 用刚刚的StandardScaler对象来进行归一化
test_feature = scaler.transform(np.array(test_feature).reshape(45, 13))
# 生成K近邻分类器
clf = KNeighborsClassifier()
# 训练分类器
clf.fit(train_feature, train_label)
# 进行预测
predict_result = clf.predict(test_feature)
return predict_result
# # 实例化一个 StandardScaler 对象
# scaler = StandardScaler()
# # scaler.fit_transform 会将数据进行标准化, 同时记录数据的均值和方差以便对后续测试数据执行同样的标准化
# std_train_feature = scaler.fit_transform(train_feature)
#
# # 实例化一个KNN分类器
# classifier = KNeighborsClassifier()
# # 使用标准化后的数据训练他
# classifier.fit(std_train_feature, train_label)
#
# # 返回(使用(训练过的分类器)预测(标准化后的数据)的结果)
# return classifier.predict(scaler.transform(test_feature))
# ********* End **********#
3. 总结
3.1 python使用
类的实例化:
# 实例化StandardScaler对象
scaler = StandardScaler()
# 生成K近邻分类器
clf = KNeighborsClassifier()
- 变量会成为该类实例的公共属性,所有的该类实例都可以通过 对象.属性名 的形式访问
- 函数会成为该类实例的公共方法,所有该类实例都可以通过 对象.方法名() 的形式调用方法
3.2 代码问题
# 并将结果保存到train_feature
train_feature = scaler.fit_transform(np.array(train_feature).reshape(133, 13))
# 用刚刚的StandardScaler对象来进行归一化
test_feature = scaler.transform(np.array(test_feature).reshape(45, 13))
这里我真的不懂为什么参数要这样reshape,改变参数后会报错
ValueError: cannot reshape array of size 1729 into shape (130,13)
其实基本上代码就是看第二个被注释掉的过程即可。
3.3 调用方法简要分析
3.3.1 StandardScaler缩放了什么?
随机梯度下降法对 feature scaling (特征缩放)很敏感,因此强烈建议您缩放您的数据。例如,将输入向量 X 上的每个特征缩放到 [0,1] 或 [- 1,+1], 或将其标准化,使其均值为 0,方差为 1。请注意,必须将 相同 的缩放应用于对应的测试向量中,以获得有意义的结果。使用 StandardScaler能很容易做到这一点
Feature Scaling(特征缩放)
在面对多维特征问题的时候,我们要确定这些特征具有相似的尺度,这样能帮助梯度更快地收敛。
以两个特征为例,一个尺度在0-2000,一个尺度在0-5,明显相差很大
当用梯度下降法时,所需要跌打的数量明显很大,那么当两个特征都缩放到0-1时就很快了

普遍使用这种

StandardScaler所支持的方法
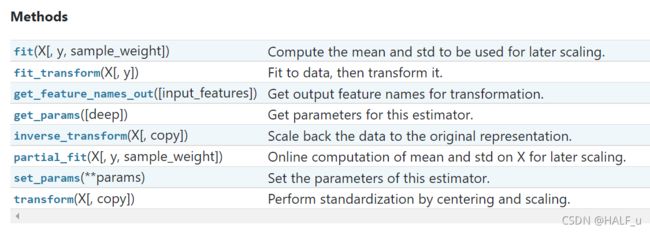
3.3.2 fit 和 fit_transform 和 transform
fit_transform 和 transform 的区别
到了这里,我们似乎知道了两者的一些差别,就像名字上的不同,前者多了一个fit数据的步骤,那为什么在标准化数据的时候不适用fit_transform()函数呢?
原因如下:
为了数据归一化(使特征数据方差为1,均值为0),我们需要计算特征数据的均值μ和方差σ^2,再使用下面的公式进行归一化:
![]()
我们在训练集上调用fit_transform(),其实找到了均值μ和方差σ^2,即我们已经找到了转换规则,我们把这个规则利用在训练集上,同样,我们可以直接将其运用到测试集上(甚至交叉验证集),所以在测试集上的处理,我们只需要标准化数据而不需要再次拟合数据。用一幅图展示如下:

fit 和 fit_transform 的区别
fit(x,y)在新手入门的例子中比较多,但是这里的fit_transform(x)的括号中只有一个参数,这是为什么呢?
fit(x,y)传两个参数的是有监督学习的算法,fit(x)传一个参数的是无监督学习的算法,比如降维、特征提取、标准化。
第3关:莫名其妙地把前两关拆分成六关来写……
1. KNN算法再学习
1.1 简介
kNN算法属于监督学习,监督学习所需要做的是在给定一部分带有特征和标签两部分数据的情况下,根据这一部分的特征和数据建立一个模型,之后当我们输入新的特征时,这个模型可以返回这种特征所应该贴上的标签。
- 计算待测数据与已有的数据之间的距离;
- 按照距离的递增关系排序;
- 选取距离最小的K个点;
- 取这K个点中的最多的类别作为待测数据的类别。
算法步骤虽然有4步,但用一句话就能说明白。kNN算法判定待测数据属于哪个类别的依据就是根据离它最近的k个点的类别。哪个类别多,它就属于哪个类别。很深刻的体现了“近朱者赤,近墨者黑”的思想。

如图所示,当我们设定K为3时,离绿色的待测点最近的3个点的类别分别为蓝色,红色,红色。由于蓝红的比分是1:2,所以绿色的待测点属于红色类。
当设定K为5时,离绿色的待测点最近的5个点的类别分别为红色、红色、蓝色、蓝色、蓝色。蓝红的比分是3:2,所以绿色的待测点属于蓝色类。
1.2 kNN算法的优缺点
任何事物都有优缺点,kNN算法也不例外。kNN算法的优点有:
- 理解简单,数学知识基本为0;
- 既能用于分来,又能用于回归;
- 支持多分类。
kNN算法可以用于回归,回归的思路是将离待测点最近的k个点的平均值作为待测点的回归预测结果。
kNN算法在测试阶段是看离待测点最近的k个点的类别比分,所以不管训练数据中有多少种类别,都可以通过类别比分来确定待测点类别。
注意:当然会有类别比分打平的情况,这种情况下可以看待测点离哪个类别最近,选最近的类别作为待测点的预测类别。
当然kNN算法的缺点也很明显,就是当训练集数据量比较大时,预测过程的效率很低。这是因为kNN算法在预测过程中需要计算待测点与训练集中所有点的距离并排序。可想而知,当数据量比较大的时候,效率会奇低。对于时间敏感的业务不太适合。
2. 使用sklearn中的kNN算法进行分类
2.1 更进一步了解K近邻算法
在kNN算法中,待分析样本的类别是由离其最近的K个样本的类别来决定的。所以kNN算法所考虑到的历史数据信息是很少的,基本只由K值的选择以及距离函数的选择来决定。当K值比较大时,所能考虑到的样本数目会更多,但是kNN算法的初衷,“近朱者赤,近墨者黑”的基本思想就无法得到运用了。而当K值比较小时,所能考虑到的样本数量就很少,这时kNN算法在噪音比较多的数据里效果很差。
除了K值之外,kNN算法的另一个核心参数是距离函数的选择。虽然在上一个实训的描述中,我们是用图片来举例说明kNN算法的。但实际上这里所说的距离与我们日常生活中所意识到的距离是不同的。在日常生活中我们所说的距离往往是欧氏距离,也即平面上两点相连后线段的长度。
欧氏距离的定义如下: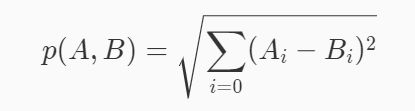
除此之外,在机器学习中常见的距离定义有以下几种:
- 汉明距离:两个字符串对应位置不一样的个数。汉明距离是以理查德·卫斯里·汉明的名字命名的。在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数;
- 马氏距离:表示数据的协方差距离。计算两个样本集相似度的距离;
- 余弦距离:两个向量的夹角作为一种判别距离的度量;
- 曼哈顿距离:两点投影到各轴上的距离总和;
- 切比雪夫距离:两点投影到各轴上距离的最大值;
- 标准化欧氏距离: 欧氏距离里每一项除以标准差。
还有一种距离叫闵可夫斯基距离,如下:

虽然一下子介绍了很多,但大家肯定还是觉得不明就里,但是不用着急,距离的定义在机器学习中是一个核心概念,在之后的学习中还会经常遇到它。在这里介绍距离的目的一个是为了让大家使用k近邻算法时,如果发现效果不太好时,可以通过使用不同的距离定义来尝试改进算法的性能。
2.2 了解sklearn中KNeighborsClassifier的参数
想要使用sklearn中使用kNN算法,只需要如下的代码(其中train_feature、train_label和test_feature分别表示训练集数据、训练集标签和测试集数据):
from sklearn.neighbors import KNeighborsClassifier
clf=KNeighborsClassifier() #生成K近邻分类器
clf.fit(train_feature, train_label) #训练分类器
predict_result=clf.predict(test_feature) #进行预测
当我们的kNN算法需要不同的参数时,上面的代码就不能满足我的需要了。所需要做的改变是在clf=KNeighborsClassifier()这一行中。KNeighborsClassifier()的构造函数其实还是有其他参数的。
比较常用的参数有以下几个:
- n_neighbors,即K近邻算法中的K值,为一整数,默认为5;
- metric,距离函数。参数可以为字符串(预设好的距离函数)或者是callable(可调用对象,大家不明白的可以理解为函数即可)。默认值为闵可夫斯基距离;
- p,当metric为闵可夫斯基距离公式时,上文中的q值,默认为2。
2.3 编程要求+测试说明
请仔细阅读右侧代码,根据方法内的提示,在Begin - End区域内进行代码补充,具体任务如下:
- 完成classification函数。函数需要完成的功能是使用KNeighborsClassifier对test_feature进行分类。其中函数的参数如下:
- train_feature: 训练集数据;
- train_label: 训练集标签;
- test_feature: 测试集数据。
补充完代码后,点击测评,平台会对你编写的代码进行测试,当你的结果与预期输出一致时,即为通过。
平台会对你返回的预测结果来计算准确率,你只需完成classification函数即可。准确率高于0.75视为过关。
预期输出:你的准确率高于0.75
2.4 实现代码
from sklearn.neighbors import KNeighborsClassifier
def classification(train_feature, train_label, test_feature):
'''
使用KNeighborsClassifier对test_feature进行分类
:param train_feature: 训练集数据
:param train_label: 训练集标签
:param test_feature: 测试集数据
:return: 测试集预测结果
'''
#********* Begin *********#
# 实例化一个KNN分类器
classifier = KNeighborsClassifier()
# 使用标准化后的数据训练他
classifier.fit(train_feature, train_label)
# 返回(使用(训练过的分类器)预测(标准化后的数据)的结果)
return classifier.predict(test_feature)
#********* End *********#
3. 使用sklearn中的kNN算法进行回归
3.1 在sklearn中使用KNeighborsRegressor
在使用kNN算法进行分类器时,我们是这样子使用sklearn库的:
from sklearn.neighbors import KNeighborsClassifier
clf=KNeighborsClassifier() #生成K近邻分类器
clf.fit(train_feature, train_label) #训练分类器
predict_result=clf.predict(test_feature) #进行预测
而对应的,当我们需要使用kNN算法进行回归器时,只需要把KNeighborsClassifier换成KNeighborsRegressor即可。代码如下:
from sklearn.neighbors import KNeighborsRegressor
clf=KNeighborsRegressor() #生成K近邻分类器
clf.fit(train_feature, train_label) #训练分类器
predict_result=clf.predict(test_feature) #进行预测
KNeighborsRegressor和KNeighborsClassifier的参数是完全一样的,所以在优化模型时可以参考上一关的内容。
3.2 编程要求+测试说明
完成regression函数。函数需要完成的功能是使用KNeighborsRegressor对test_feature进行分类。其中函数的参数如下:
- train_feature: 训练集数据;
- train_label: 训练集标签;
- test_feature: 测试集数据。
平台会对你返回的预测结果来计算准确率,你只需完成regression函数即可。r2 score高于0.75视为过关。
预期输出:你的r2 score高于0.75。
3.3 代码实现
from sklearn.neighbors import KNeighborsRegressor
def regression(train_feature, train_label, test_feature):
'''
使用KNeighborsRegressor对test_feature进行分类
:param train_feature: 训练集数据
:param train_label: 训练集标签
:param test_feature: 测试集数据
:return: 测试集预测结果
'''
#********* Begin *********#
# 生成K近邻分类器
clf=KNeighborsRegressor()
# 训练分类器
clf.fit(train_feature, train_label)
# 进行预测
return clf.predict(test_feature)
#********* End *********#
4. 分析红酒数据
4.1 背景知识补充
sklearn中已经内置的红酒数据,获取红酒数据的代码如下:
from sklearn.datasets import load_wine
wine_dataset = load_wine()
# 打印红酒数据集中的特征的名称
print(wine_dataset['feature_names'])
打印结果如下:
['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
从打印结果可以看出,该数据集中包含了红酒的酒精含量、苹果酸含量、颜色饱和度等信息。
同样我们可以看下红酒的标签名称,代码如下:
from sklearn.datasets import load_wine
wine_dataset = load_wine()
# 打印红酒数据集中的标签的名称
print(wine_dataset['target_names'])
打印结果如下:
['class_0' 'class_1' 'class_2']
可以看出该数据集中红酒的种类总共为3类。也就是说如果用机器学习算法来对其进行分类的话,属于多分类问题。而我们所学习的kNN算法正好可以解决多分类问题。
4.2 编程要求+测试说明
请仔细阅读右侧代码,根据方法内的提示,在Begin - End区域内进行代码补充,完成alcohol_mean函数。该函数需要完成返回红酒数据中的平均酒精含量。其中函数的参数解释如下:
- data:红酒数据对象。
补充完代码后,点击测评,平台会对你编写的代码进行测试,当你的结果与预期输出一致时,即为通过。
预期输出:平均酒精含量计算正确。
4.3 代码实现
import numpy as np
def alcohol_mean(data):
'''
返回红酒数据中红酒的酒精平均含量
:param data: 红酒数据对象
:return: 酒精平均含量,类型为float
'''
#********* Begin *********#
# 取第一列数据,求平均数
return data.data[:,0].mean()
# 字典,就是data['data'].mean(0)
#********* End **********#
5. 对数据进行标准化
5.1 标准化相关知识
我们可以计算以下红酒数据中每个特征所对应的均值和标准差,代码如下:
from sklearn.datasets import load_wine
wine_dataset = load_wine()
print(wine_dataset.data.mean(0))
print(wine_dataset.data.std(0))
打印结果如下:
[1.30006180e+01 2.33634831e+00 2.36651685e+00 1.94949438e+01 9.97415730e+01 2.29511236e+00 2.02926966e+00 3.61853933e-01 1.59089888e+00 5.05808988e+00 9.57449438e-01 2.61168539e+00 7.46893258e+02]
[8.09542915e-01 1.11400363e+00 2.73572294e-01 3.33016976e+00 1.42423077e+01 6.24090564e-01 9.96048950e-01 1.24103260e-01 5.70748849e-01 2.31176466e+00 2.27928607e-01 7.07993265e-01 3.14021657e+02]
从打印结果可以看出,有的特征的均值和标准差都比较大,例如如最后一个特征。如果现在用kNN算法来对这样的数据进行分类的话,kNN算法会认为最后一个特征比较重要。因为假设有两个样本的最后一个特征值分别为1和100,那么这两个样本之间的距离可能就被这最后一个特征决定了。这样就很有可能会影响kNN算法的准确度。为了解决这种问题,我们可以对数据进行标准化。
标准化的手段有很多,而最为常用的就是StandardScaler。StandardScaler通过删除平均值和缩放到单位方差来标准化特征,并将标准化的结果的均值变成0,标准差为1。
假设标准化后的特征为z,标准化之前的特征为x,特征的均值为μ,方差为s。则StandardScaler可以表示为z=(x−μ)/s。
sklearn中已经提供了StandardScaler的接口,使用代码如下:
from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
# 实例化StandardScaler对象
scaler = StandardScaler()
# 用data的均值和标准差来进行标准化,并将结果保存到after_scaler
after_scaler = scaler.fit_transform(data)
# 用刚刚的StandardScaler对象来进行归一化
after_scaler2 = scaler.transform([[2, 2]])
print(after_scaler)
print(after_scaler2)
打印结果如下:
[[-1. -1.]
[-1. -1.]
[ 1. 1.]
[ 1. 1.]]
[[3. 3.]]
5.2 编程要求+测试说明
请仔细阅读右侧代码,根据方法内的提示,在Begin - End区域内进行代码补充,完成scaler函数。该函数需要完成是返回标准化后的数据。其中函数的参数解释如下:
- data:红酒数据对象。
补充完代码后,点击测评,平台会对你编写的代码进行测试,当你的结果与预期输出一致时,即为通过。
预期输出:标准化成功
5.3 代码实现
from sklearn.preprocessing import StandardScaler
import numpy as np
def scaler(data):
'''
返回标准化后的红酒数据
:param data: 红酒数据对象
:return: 标准化后的红酒数据,类型为ndarray
'''
#********* Begin *********#
# 实例化StandardScaler对象
scaler = StandardScaler()
# 进行标准化,并将结果保存
return scaler.fit_transform(data['data'])
#********* End **********#
6. 使用kNN算法进行预测
6.1 编程要求+测试说明
请仔细阅读右侧代码,根据方法内的提示,在Begin - End区域内进行代码补充,完成classification函数。该函数需要完成是对测试数据进行红酒分类,并将分类结果返回。其中函数的参数解释如下:
- train_feature:训练集数据,类型为ndarray;
- train_label:训练集标签,类型为ndarray;
- test_feature:测试集数据,类型为ndarray。
补充完代码后,点击测评,平台会对你编写的代码进行测试,当你的结果与预期输出一致时,即分类准确率高于0.92视为过关。
预期输出:你的分类准确率高于0.92。
6.2 代码实现
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
def classification(train_feature, train_label, test_feature):
'''
对test_feature进行红酒分类
:param train_feature: 训练集数据,类型为ndarray
:param train_label: 训练集标签,类型为ndarray
:param test_feature: 测试集数据,类型为ndarray
:return: 测试集数据的分类结果
'''
#********* Begin *********#
# 实例化StandardScaler对象
scaler = StandardScaler()
# 标准化, 同时记录数据的均值和方差以便对后续测试数据执行同样的标准化
tr_feature = scaler.fit_transform(train_feature)
te_feature = scaler.transform(test_feature)
# 生成K近邻分类器
clf = KNeighborsClassifier()
# 训练分类器
clf.fit(tr_feature, train_label)
# 进行预测
predict_result = clf.predict(te_feature)
return predict_result
#********* End **********#