计算机视觉(二):图像分类-分类器及损失
计算机视觉笔记总目录
1.CIFAR-10例子介绍
图像分类数据集示例:CIFAR-10,一个流行的图像分类数据集。这个数据集由60000个32像素高和宽组成的小图像组成。每个图像都被标记为10个类之一(例如“飞机、汽车、鸟等”)。这60000个图像被分割成50000个图像的训练集和10000个图像的测试集。在下图中,您可以看到10个类中每个类的10个随机示例图像:

上面图中就是数据集的类别和图像的示例,右边展示了一部分测试图像以及最相近的在训练集中前10张图片集合。
1.1算法思路
假设现在我们得到了cifar-10训练集,它包含50000个图像(每个标签有5000个图像),我们希望标记预测剩下的10000个图像。
- 最近邻分类器将得到一个测试图像,将其与每个训练图像进行比较,并预测其标签,为最近的训练图像的标签。
在上面和右边的图像中,您可以看到10个示例测试图像的这种过程的示例结果。注意,在大约10个示例中,只有3个检索到同一类的图像,而在其他7个示例中则不是这样。例如,在第8排,离马头最近的训练图像是一辆红色的汽车,大概是由于强烈的黑色背景。因此,在这种情况下,马的图像会被错误地标记为汽车。
如何比较图像两张图片
每个图像都是32 x 32 x 3的像素。最简单的方法之一是逐像素比较图像,并将所有差异相加。换句话说,给定两个图像并将其表示为向量 I 1 I_1 I1, I 2 I_2 I2,比较它们的合理选择可能是L1距离:
d 1 ( I 1 , I 2 ) = ∑ p ∣ I 1 p − I 2 p ∣ d_1 (I_1, I_2) = \sum_{p} \left| I^p_1 - I^p_2 \right| d1(I1,I2)=p∑∣I1p−I2p∣
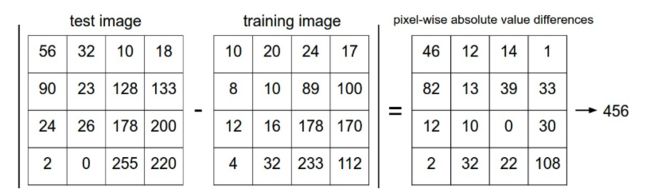
如果两个图像一样,结果为0,如果两个图像相差很大,结果会很大
训练数据集与测试数据L1距离代码实现:
distances = np.sum(np.abs(Xtrain - Xtest[i,:]), axis = 1)
设定输入的图片和标签形状为
Xtrain_rows = Xtrain.reshape(Xtrain.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xtest_rows = Xtest.reshape(Xtest.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072
完整代码实现(Numpy)
import numpy as np
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, y):
"""
X:N x D形状,N为样本数,D为像素数量
Y:1维,大小为N
"""
# 所有最近邻需要的训练数据集
self.Xtrain = X
self.ytrain = y
def predict(self, Xtest):
"""对输入的X若干个测试图片,每个进行预测"""
num_test = Xtest.shape[0]
# 确保输出类型一样
Ypred = np.zeros(num_test, dtype = self.ytrain.dtype)
# 循环所有测试数据
for i in range(num_test):
# 使用L1距离找到i最近的训练图片
distances = np.sum(np.abs(self.Xtrain - Xtest[i,:]), axis = 1)
min_index = np.argmin(distances)# 获取最近的距离的图像下标
Ypred[i] = self.ytrain[min_index]# 预测标签(获取对应训练那张图片的目标标签)
return Ypred
结果
使用上述方法,我们在CIFAR-10的测试机上面只能达到38.6% 的准确率,距离目前人类的测试结果(大概)94%的准确率,还有后面着重介绍的state of the art (SOTA,前沿的) 的卷积神经网络取得的效果95%
距离选择
距离有很多种方式,在计算两个向量的距离时候,也可以选择L2,欧式距离。
d 2 ( I 1 , I 2 ) = ∑ p ( I 1 p − I 2 p ) 2 d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 - I^p_2 \right)^2} d2(I1,I2)=p∑(I1p−I2p)2
只要去修改其中的距离计算即可
distances = np.sqrt(np.sum(np.square(Xtrain - Xtest[i,:]), axis = 1))
但是在实际的最近邻应用程序中,我们可以省略平方根操作,因为平方根是单调函数。缩放距离的绝对大小,因此有或没有顺序的最近邻是相同的。如果您使用L2距离在cifar-10上运行最近邻分类器,将获得35.4%的精度(略低于L1距离结果)。
L1和L2哪个好,没有明确的方法,具体问题具体分析,不断尝试
2.线性分类
现在,我们将开发一种功能更强大的图像分类方法,最终将其自然地扩展到整个神经网络和卷积神经网络。线性分类方法。这种方法来主要由两部分,一个函数将输入数据映射到一个类别分数,另一个就是损失函数来量化预测的分数与目标值之间的一致性。
回到CIFAR-10例子,输入训练图像的数据集50000张图片, 向量维度D = 32 x 32 x 3 = 3072像素,K大小为10个类别
x i ∈ R D , i = 1 x_i ∈ R^D,i=1 xi∈RD,i=1
定义这样的函数为
f : R D ↦ R K f ( x i , W , b ) = W x i + b f:R^D ↦ R^K\\f(x_i,W,b) = Wx_i + b f:RD↦RKf(xi,W,b)=Wxi+b
我们可以控制参数w,b的设置。我们的目标是设置这些参数,以便计算出的分数与整个训练集中的目标值标签相匹配。这种方法的一个优点是利用训练数据来学习参数w,b,但是一旦学习完成,我们就可以丢弃整个训练集,只保留学习到的参数。
2.1 线性分类解释

例子:为了方便看见,假设图像只有4个像素(4个单色像素,这里为了简单,不考虑3通道颜色),并且我们有3个类(猫(CAT)、狗(DOG)、轮船(SHIP)。我们将图像像素拉伸成一列,然后进行矩阵乘法得到每个类的分数。 y = W x + b = [ 3 , 4 ] ∗ [ 4 , 1 ] + [ 3 , 1 ] = [ 3 , 1 ] y=Wx+b=[3, 4]*[4, 1] + [3, 1] = [3, 1] y=Wx+b=[3,4]∗[4,1]+[3,1]=[3,1]。上图图中的权重计算结果结果并不好,权重会给我们的猫图像分配一个非常低的猫分数。得出的结果偏向于狗。
如果可视化分类,我们为了方便,将一个图片理解成一个二维的点,在下面坐标中显示如下:
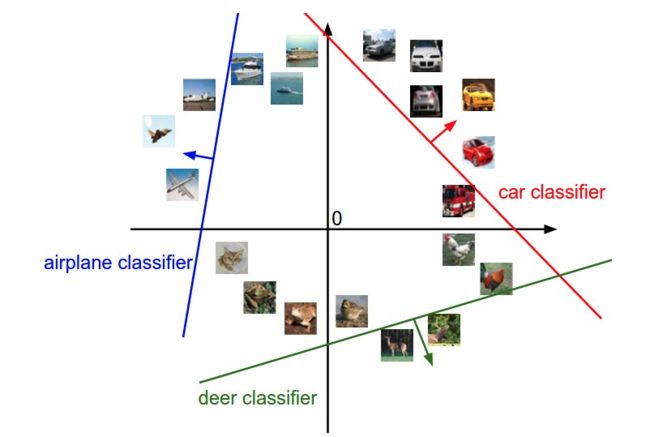
-
解释:w的每一行都是其中一个类的分类器。这些数字的几何解释是,当我们改变w的一行时,像素空间中相应的线将以不同的方向旋转。而其中的偏置是为了让我们避免所有的分类器都过原点。
-
总结:分类器的权重矩阵其实是对应分类的经过训练得到的一个分类模板,通过测试数据与分类模板间的数据计算来进行分类。在训练的过程中,其实可以看作是权重矩阵的学习过程,也可以看成是分类模板的学习过程,如何从训练样本中学习分类的模板。模板权重的大小,反映了样本中每个像素点对分类的贡献率
学习到的权重
将线性分类器解释为模板匹配。权重w的另一种解释是,w的每一行对应于其中一个类的模板(有时也称为原型)。然后,通过使用内部积(或点积)逐个比较每个模板和图像来获得图像的每个类的分数,以找到“最适合”的模板。我们以CIFAR-10例子,10个类别分类,学习到10个模板,下方显示的即是训练过后所学习的权重矩阵(也即是分类模板)

线性分类器将数据中这两种模式的马合并到一个模板中。类似地,汽车分类器似乎已经将多个模式合并到一个模板中,该模板必须从各个方面识别所有颜色的汽车。特别是,这个模板最终是红色的,这意味着cifar-10数据集中的红色汽车比任何其他颜色的都多。线性分类器太弱,无法正确解释不同颜色的汽车,但正如我们稍后将看到的,神经网络将允许我们执行这项任务。
存在问题:
- 每个类别,只能学习到一个模板,分类能力是有限的,如果数据集中的图片同一类别差差异较大,那么学习不到太多的东西来进行判别。
- 无法进行非线性的分类(类似于异或的分类)[后面会介绍]
2.2 损失函数
损失函数是用来告诉我们当前分类器性能好坏的评价函数,是用于指导分类器权重调整的指导性函数,通过该函数可以知道该如何改进权重系数。CV与深度学习课程之前,大家应该都接触过一些损失函数了,例如解决二分类问题的逻辑回归中用到的对数似然损失、SVM中的合页损失等等。
- 对数似然损失
L ( y , y ^ ) = − y log y ^ − ( 1 − y ) log ( 1 − y ^ ) L(y, \hat y)=-y\log\hat y-(1-y)\log(1-\hat y) L(y,y^)=−ylogy^−(1−y)log(1−y^) - 合页损失
L i = ∑ j ≠ y i max ( 0 , s j − s y i + Δ ) L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta) Li=j=yi∑max(0,sj−syi+Δ)
现在回到前面的线性分类例子,该函数预测在“猫”、“狗”和“船”类中的分数,我们发现,在这个例子中,我们输入描绘猫的像素,但是猫的分数与其他类别(狗的分数437.9和船的分数61.95)相比非常低(-96.8)。那么这个结果并不好,我们将会去衡量这样的一个成本,如果分类做好了,这个损失将会减少。
多分类问题的损失该如何去衡量?下面会进行通常会使用的两种方式作对比,这里介绍在图像识别中最常用的两个损失——多类别SVM损失(合页损失hinge loss)和交叉熵损失,分别对应多类别SVM分类器和Softmax分类器
2.2.1 多分类SVM损失
函数通过函数 f ( x i , W ) f(x_i, W) f(xi,W)计算分数,我们在这里简写成 s s s,对于某个 i i i样本,某个 j j j目标类别分数记做 s j = f j ( x i , W ) s_j = f_j(x_i, W) sj=fj(xi,W)
得到:
L i = ∑ j ≠ y i max ( 0 , s j − s y i + Δ ) L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta) Li=j=yi∑max(0,sj−syi+Δ)
我们正针对于前面简化例子,来复习理解下SVM损失,下图使我们得到的线性模型预测分数结果

-
求SVM损失
对于第一张图片来讲,损失计算为
L i = ∑ j ≠ y i max ( 0 , s j − s y i + Δ ) = max ( 0 , 5.1 − 3.2 + 1 ) + max ( 0 , − 1.7 − 3.2 + 1 ) = max ( 0 , 2.9 ) + max ( 0 , − 3.9 ) = 2.9 + 0 = 2.9 L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)=\max(0, 5.1 -3.2 +1)+\max(0, -1.7-3.2 +1) = \max(0, 2.9) + \max(0, -3.9) = 2.9 + 0 = 2.9 Li=j=yi∑max(0,sj−syi+Δ)=max(0,5.1−3.2+1)+max(0,−1.7−3.2+1)=max(0,2.9)+max(0,−3.9)=2.9+0=2.9
那么同理第二张图片的损失为
L i = ∑ j ≠ y i max ( 0 , s j − s y i + Δ ) = max ( 0 , 1.3 − 4.9 + 1 ) + max ( 0 , 2.0 − 4.9 + 1 ) = max ( 0 , − 2.6 ) + max ( 0 , − 1.9 ) = 0 + 0 = 0 L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)=\max(0, 1.3 -4.9 +1)+\max(0, 2.0-4.9 + 1) = \max(0, -2.6) + \max(0, -1.9) = 0 + 0 =0 Li=j=yi∑max(0,sj−syi+Δ)=max(0,1.3−4.9+1)+max(0,2.0−4.9+1)=max(0,−2.6)+max(0,−1.9)=0+0=0

最后一个损失结果
L i = ∑ j ≠ y i max ( 0 , s j − s y i + Δ ) = max ( 0 , 2.2 − ( − 3.1 ) + 1 ) + max ( 0 , 2.5 − ( − 3.1 ) + 1 ) = max ( 0 , 6.3 ) + max ( 0 , 6.6 ) = 6.3 + 6.6 = 12.9 L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)=\max(0, 2.2 -(-3.1) +1)+\max(0, 2.5-(-3.1) + 1) = \max(0, 6.3) + \max(0, 6.6) = 6.3+6.6=12.9 Li=j=yi∑max(0,sj−syi+Δ)=max(0,2.2−(−3.1)+1)+max(0,2.5−(−3.1)+1)=max(0,6.3)+max(0,6.6)=6.3+6.6=12.9 -
平均合页损失
L = 1 N ∑ i = 1 N L i = ( 2.9 + 0 + 12.9 ) 3 = 5.27 L= \frac{1}{N} \sum_{i=1}^{N}L_{i} = \frac{(2.9+0+12.9)}{3}=5.27 L=N1i=1∑NLi=3(2.9+0+12.9)=5.27
最终得到5.27的分数大小,Loss反映了真实分类所得分数与其他分类分数的差别,也就是说,如果真实分类所得分数比分类为其他类的分数要低,但是分数低多少,要想真实分类的分数最高,差距在哪,即是通过损失函数的l值反映出来了。同时,如果分类正确的分数比其他的分类分数高于1,即使正确分类的分数发生微小变化(相差仍然大于1),那么Hinge Loss仍然有效,损失函数值不会发生变化。

多分类支持向量机损失希望正确分类的分数至少高于其他分类的分数,如果错误分类的分数-正确分类的分数很小即超过上述的红色区域,则不会加入损失;如果在红色区域内部,那么会累积损失。
当然这里为了方便理解,并没有去考虑正则化项的影响,有时候使用L2-SVM损失效果会更好些。
关于深度学习的正则化后面会着重去介绍
2.2.2 Softmax 分类(Multinomial Logistic Regression)与cross-entropy(交叉熵损失)
1、Softmax
另外一种就是Softmax,它有着截然不同的损失函数。如果你听说过逻辑回归二分类器,那么Softmax分类器是它泛化到多分类的情形。不像SVM那样会得到某个分类的分数,softmax会给出一个更加合适的输入即归一化的类别概率
-
公式:
y = e f y i ∑ j e f j y = \frac{e^{f_{y_i}}}{ \sum_j e^{f_j} } y=∑jefjefyi- f j f_j fj为分数向量中第 j j j个类别分数
- f j ( z ) = e z j ∑ k e z k f_j(z) = \frac{e^{z_j}}{\sum_k e^{z_k}} fj(z)=∑kezkezj称之为softmax函数,会将输出结果缩小到0到1的一个值,并且所有值相加为1
理解:Softmax函数接收一组评分输出s(有正有负),对每个评分sk进行指数化确保正数,分母是所有评分指数化的和,分子是某个评分指数化后的值,这样就起到了归一化的作用。某个类的分值越大,指数化后越大,函数输出越接近于1,可以把输出看做该类别的概率值,所有类别的概率值和为一。
-
计算例子:
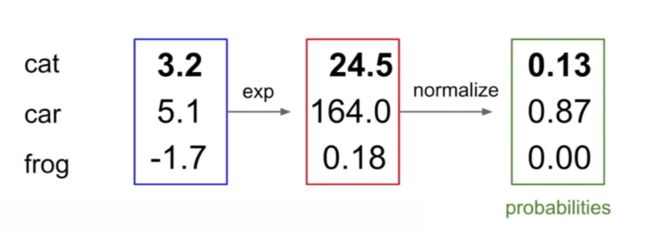
P ( c a t ∣ s c o r e ) = e 3.2 / ( e 3.2 + e 5.1 + e − 1.7 ) = 0.13 P ( c a r ∣ s c o r e ) = e 5.1 / ( e 3.2 + e 5.1 + e − 1.7 ) = 0.87 P ( f r o g ∣ s c o r e ) = e − 1.7 / ( e 3.2 + e 5.1 + e − 1.7 ) = 0.00 P(cat|score) = e^{3.2}/(e^{3.2}+e^{5.1}+e^{-1.7}) = 0.13\\ P(car|score) = e^{5.1}/(e^{3.2}+e^{5.1}+e^{-1.7}) = 0.87\\ P(frog|score) = e^{-1.7}/(e^{3.2}+e^{5.1}+e^{-1.7}) = 0.00 P(cat∣score)=e3.2/(e3.2+e5.1+e−1.7)=0.13P(car∣score)=e5.1/(e3.2+e5.1+e−1.7)=0.87P(frog∣score)=e−1.7/(e3.2+e5.1+e−1.7)=0.00 -
单个样本 i i i分类的矢量计算表达式
o ( i ) = x ( i ) W + b , y ^ ( i ) = softmax ( o ( i ) ) \begin{aligned} {o}^{(i)} &= {x}^{(i)} {W} + {b},\\ {\hat{y}}^{(i)} &= \text{softmax}({o}^{(i)}) \end{aligned} o(i)y^(i)=x(i)W+b,=softmax(o(i)) -
批量样本分类的矢量计算表达式
设批量特征为 X ∈ R n × d {X} \in \mathbb{R}^{n \times d} X∈Rn×d,假设softmax的权重和偏差参数分别为 W ∈ R d × q {W} \in \mathbb{R}^{d \times q} W∈Rd×q和 b ∈ R 1 × q {b} \in \mathbb{R}^{1 \times q} b∈R1×q,softmax的矢量计算表达式为
O = X W + b , Y ^ = softmax ( O ) \begin{aligned} {O} &= {X} {W} + {b},\\ {\hat{Y}} &= \text{softmax}({O}) \end{aligned} OY^=XW+b,=softmax(O)
2、cross-entropy
交叉熵损失是应用softmax分类之后如何计算损失大小的一种方式,这种方式就来源于信息论理论。
-
公式:
H ( p , q ) = − ∑ x p ( x ) log q ( x ) H(p,q) = - \sum_x p(x) \log q(x) H(p,q)=−x∑p(x)logq(x)- 衡量某个真实分布pp与预估的分布qq之间交叉损失
- q就是我们计算出来的归一化分类概率
q = e f y i / ∑ j e f j q = e^{f_{y_i}} / \sum_j e^{f_j} q=efyi/j∑efj
1、信息论的理解: 交叉熵另外也可以改写成: H ( p , q ) = H ( p ) + D K L ( p ∣ ∣ q ) H(p,q) = H(p) + D_{KL}(p||q) H(p,q)=H(p)+DKL(p∣∣q),P的熵加上KL距离/Kullback-Leibler Divergence,而P的熵为0,所以也就等同于最小化两个分部之间的KL距离
2、概率的角度理解: 我们在做的事情,就是最小化错误类别的负log似然概率,也可以理解为进行最大似然估计(Maximum Likelihood Estimation ,MLE)。这个时候我们的正则化项有很好的解释性,可以理解为整个损失函数在权重矩阵W上的一个高斯先验,所以其实这时候是在做一个最大后验估计(Maximum a posteriori ,MAP)
-
例子理解:对于真实值会进行一个one-hot编码,每一个样本的所属类别都会在某个类别位置上标记, p = [ 0 , … 1 , … , 0 ] p = [ 0 , … 1 , … , 0 ] p = [0, \ldots 1, \ldots, 0]p=[0,…1,…,0] p=[0,…1,…,0]p=[0,…1,…,0]

它的损失如何计算?0log(0.10)+0log(0.05)+0log(0.15)+0log(0.10)+0log(0.05)+0log(0.20)+1log(0.10)+0log(0.05)+0log(0.10)+0log(0.10)即为
1log(0.10)在概率的角度理解,我们在做的事情,就是最小化错误类别的负log似然概率,也可以理解为进行最大似然估计/Maximum Likelihood Estimation (MLE)
-
存在问题:数据稳定性
在实际编写工程实现的时候,计算softmax函数的中间项 e f y i e^{f_{y_i}} efyi, ∑ j e f j \sum_j e^{f_j} ∑jefj 可能会非常大。进行巨大数据的出发会使得数据不稳定,所以使用一个归一化优化非常重要。
解决方式:在分子和分母中加入一个常数C,加入到求和中,得到下面的式子
e f y i ∑ j e f j = C e f y i ∑ j C e f j = e f y i + log C ∑ j e f j + log C \frac{e^{f_{y_i}}}{\sum_j e^{f_j}} = \frac{Ce^{f_{y_i}}}{\sum_j Ce^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}} ∑jefjefyi=∑jCefjCefyi=∑jefj+logCefyi+logC
C 的取值由我们而定,不影响最后的结果,但是对于实际计算过程中的稳定性有很大的帮助。一个最常见的C取值为 log C = − max j f j \log C=-\max_j f_j logC=−maxjfj 这表明我们平移了每个分数值,使得最终指数e的幂中的最大值为0.
代码实现如下:
# 三个类别分类,并且得到的分数大小
f = np.array([123, 456, 789])
# 1、直接这样计算会存在指数爆炸问题
p = np.exp(f) / np.sum(np.exp(f))
# 2、进行分数平移,得到最大值0
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f))
2.3 SVM与Softmax对比
下面这张图就清楚的展示了两个分类以及其损失计算方式的区别
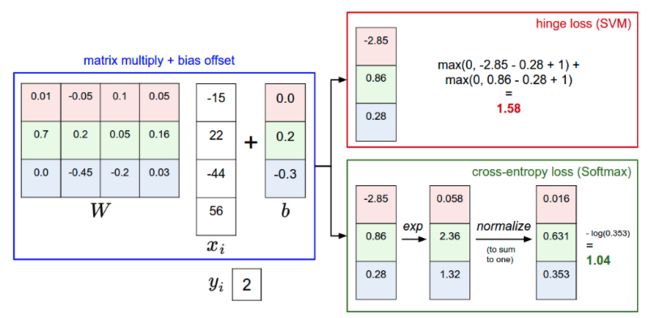
实际应用中,两类分类器的表现是相当的,两者差异较小。每个人都回去根据那个表现更好来做选择。如果要对比的话,其中的一些差异如下:
- SVM下,我们能完成类别的判定,但是实际上我们得到的类别得分,大小顺序表示着所属类别的排序,但是得分的绝对值大小并没有特别明显的物理含义
- SVM可能拿到对应 猫/狗/船 的得分[12.5, 0.6, -23.0],同一个问题,Softmax分类器拿到[0.9, 0.09, 0.01]。这样在SVM结果下我们只知道猫是正确答案,而在Softmax分类器的结果中,我们可以知道属于每个类别的概率
- Softmax分类器中,结果的绝对值大小表征属于该类别的概率
- 1、比如说SVM损失设定 Δ = 1 \Delta=1 Δ=1,SVM只关注分类边界,如果算得的得分是[10, -2, 3],比如实际第一类是正确结果,那么10-3=7已经比1要大很多了,最后损失为0。所以它觉得这已经是一个很标准的答案了,完全满足要求了,不需要再做其他事情了,意味着 [10, -100, -100] 或者 [10, 9, 9],它都是满意的,并没有区别
- 2、对于Softmax而言,它总是觉得可以让概率分布更接近标准结果一些,交叉熵损失更小一些。 [10, -100, -100] 和 [10, 9, 9]映射到概率域,计算得到的互熵损失是有很大差别的。所以Softmax是一个永远不会满足的分类器,在每个得分计算到的概率基础上
2013年的一篇论文就针对于神经网络损失函数在CIFAR-10等数据集上进行了两种损失对比,参考:Deep Learning using Linear Support Vector Machines,这篇论文就告诉L2-SVM比Softmax效果好一些
现在我们知道了如何基于参数,将数据集中的图像映射成为分类的评分,也知道了两种不同的损失函数,它们都能用来衡量算法分类预测的质量。如何高效地得到能够使损失值最小的参数呢?这个求得最优参数的过程被称为最优化,下篇文章我们将会介绍。