手撕二叉树遍历(前序 + 中序 + 后序 递归 + 非递归 代码实现 + 例题)
文章目录
-
- 前引
- 二叉树遍历介绍
-
- 1、二叉树前序遍历
-
- 1、二叉树前序遍历代码(递归)
- 2、二叉树前序遍历代码(非递归)
- 2、二叉树中序遍历
-
- 1、二叉树中序遍历代码(递归)
- 2、二叉树中序遍历代码(非递归)
- 3、二叉树后序遍历
-
- 1、二叉树后序遍历代码(递归)
- 2、二叉树后序遍历代码(非递归)
- 二叉树遍历例题
前引
刚刚才写完了手撕最小堆的博客 就想了 是不是也得写一下二叉树遍历呢 哈哈 因为前段时间才写过 而且那个时候理解花了很多时间 所以现在手撕了三个遍历 大概花了5分钟左右 力扣三道题 前中后序遍历也就一次性全部AC啦 把这篇写了 我就去吃晚饭了惹 那进入下面的题目吧
二叉树遍历介绍
二叉树 真的是经典的不能再经典 对于其三个 非递归的遍历 必须熟练熟练的掌握! 面试肯定是非常常考的 肯定不会考你递归的 那不然也太弱智了哈哈
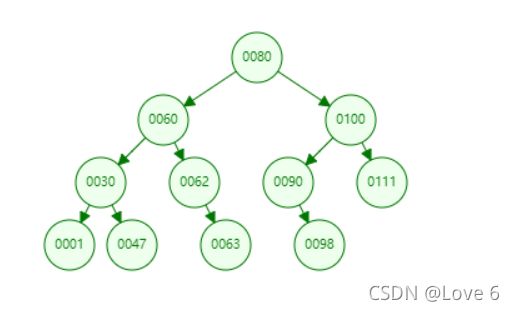
二叉树遍历 首先需要先搞清楚 什么是前序 什么是中序 什么是后序 我们后面都会用到这张图 分别再将 这里就先不说了
遍历当然不仅仅是需要用在二叉搜索树 任意的树都可以遍历 但是对于二叉搜索树的前中后序遍历的话 就有一些其他的性质了 这个后面再说
1、二叉树前序遍历
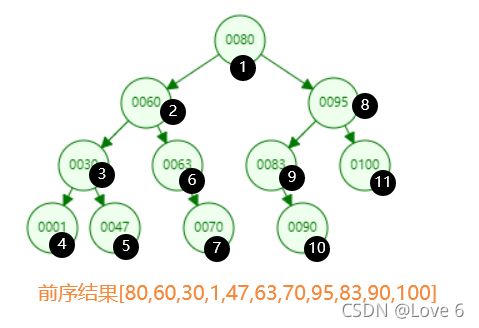
在讲代码实现前 我们把上面的前序的结果给出来
我们可以理解 我们最偏向于先输出值 然后其次是向左节点移动 最后向右节点移动 每当移动后 我们又会按照这个顺序进行动作
1、二叉树前序遍历代码(递归)
作为最经典的递归实现 递归代码如下
class Solution {
public:
void preorder_visit(TreeNode* root,vector<int>& ret)
{
if(!root) return;
ret.emplace_back(root->val);
preorder_visit(root->left,ret);
preorder_visit(root->right,ret);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ret;
preorder_visit(root,ret);
return ret;
}
};
2、二叉树前序遍历代码(非递归)
感觉我讲怎么非递归 也不好讲
我是以一种抽象的具象化来写的代码
我认为就是 前序的话 我们每当访问到一个节点时 即刻放入数组中
而遍历到最左边的时候 看是否有右边的结点 如果有 再进入循环 没有的话 也无所谓 当前指针等于nullptr进入下一轮循环即可
大家还是结合代码理解一下吧
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
TreeNode* ptr = root;
stack<TreeNode*> stack;
vector<int> ret;
while(ptr || stack.size())
{
while(ptr)
{
stack.emplace(ptr); //放入指针
ret.emplace_back(ptr->val);//即刻放入
ptr = ptr->left;
}
ptr = stack.top()->right; //访问顶部的右边指针
stack.pop(); //已经用过了 则直接pop
}
return ret;
}
};
2、二叉树中序遍历
一样的为了大家方便理解 还是花点时间我自己再做一下中序遍历的结果
中序遍历的话 我们还是直接看下面的代码吧 大家跟着这个图一起理解
1、二叉树中序遍历代码(递归)
直接给代码了
class Solution {
public:
void inorder_visit(TreeNode* root,vector<int>& ret)
{
if(!root) return;
inorder_visit(root->left,ret);
ret.emplace_back(root->val);
inorder_visit(root->right,ret);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
inorder_visit(root,ret);
return ret;
}
};
2、二叉树中序遍历代码(非递归)
这部分我还是花点时间来写吧
我的理解是 我们还是跟着递归代码来写
首先 不再是遇到节点就push数字了 而是从stack顺着递归的顺序来push如果是从stack里面出来的再push然后ptr还是一样的 从stack.top()->right没变 变得只是push数字的顺序
代码实现如下
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
TreeNode* ptr = root;
stack<TreeNode*> stack;
vector<int> ret;
while(ptr || stack.size())
{
while(ptr)
{
stack.emplace(ptr); //储存指针
ptr = ptr->left;
}
ptr = stack.top(); //倒出来指针
stack.pop(); //用过了
ret.emplace_back(ptr->val); // 把值再放进去 按照递归顺序
ptr = ptr->right; // 看看右边指针
}
return ret;
}
};
3、二叉树后序遍历
1、二叉树后序遍历代码(递归)
直接放代码了
class Solution {
public:
void postorder_visit(TreeNode* root,vector<int>& ret)
{
if(!root) return;
postorder_visit(root->left,ret);
postorder_visit(root->right,ret);
ret.emplace_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ret;
postorder_visit(root,ret);
return ret;
}
};
2、二叉树后序遍历代码(非递归)
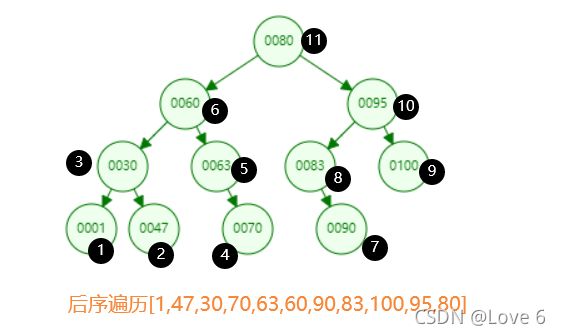
后序相对 前序与中序就不一样了一点 也要难了一点 但是只是有那么一点不同 因为我们需要直到是否当前节点已经被用尽了
对 我是这样理解的 用尽了 必须要求右边节点在当前节点前被push进入数组 如果前一个右边指针不是pre指针 那么说明右边要不就是nullptr如果是空指针 则我们可以直接推入数组了 因为说明当前这个指针已经是最后一个了
我理解的代码 也就是这样写的 写出来就是如下 不是很好理解 希望大家多花点时间理解以下代码
那最后一个就直接放代码了
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
TreeNode* ptr = root,*pre = nullptr; \\pre指针 记录前一个被推入数组
stack<TreeNode*> stack;
vector<int> ret;
while(ptr || stack.size())
{
while(ptr)
{
stack.emplace(ptr);
ptr = ptr->left;
}
ptr = stack.top();
if(!ptr->right || ptr->right == pre) //如果右边指针为空 或者右边已经被推入了 则可以直接推入
{
ret.emplace_back(ptr->val);
pre = ptr;
stack.pop();
ptr = nullptr;
}
else ptr = ptr->right;
}
return ret;
}
};
二叉树遍历例题
下面就放三个 经典前中后序的力扣题目 大家也可以去通过这三道题目去验证自己的代码是否正确 终于写完了 现在正在EDG打DK 我得赶快写了 回寝室看比赛了 太激动了 先写到这里
144. 二叉树的前序遍历
94. 二叉树的中序遍历
145. 二叉树的后序遍历
Love 6 刷题记录博客 144. 二叉树的前序遍历 (迭代 递归 Morris)
Love 6 刷题记录博客 94. 二叉树的中序遍历
Love 6 刷题记录博客 145. 二叉树的后序遍历(神级Morris)