写在前边
大家好,我是melo,一名大二上软件工程在读生,经历了一年的摸滚,现在已经在工作室里边准备开发后台项目啦。
不过这篇文章呢,还是想跟大家聊一聊数据结构与算法,学校也是大二上才开设了数据结构这门课,希望可以一边学习数据结构一边积累后台项目开发经验。
最近我们进入了排序算法专题,上节课聊到了"简单"插入排序,那在简单的基础上,我们可以怎么做进一步的优化呢,这篇来看看优化版--希尔排序!
知识点
概念
希尔排序(Shell Sort)是插入排序的一种,它是针对直接插入排序算法的改进。
希尔排序又称缩小增量排序,因 DL.hell 于 1959 年提出而得名。
它通过比较相距一定间隔的元素来进行,各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。
引入
简单插入排序存在问题
改进
- 分割待排序记录的个数,分别进行插入排序
基本思想
- 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个数组恰被分成一组,算法便终止
精髓
- 由于开始时每组只有很少整数,所以排序很快。之后每组含有的整数越来越多,但是由于这些数也越来越有序,所以排序速度也很快。
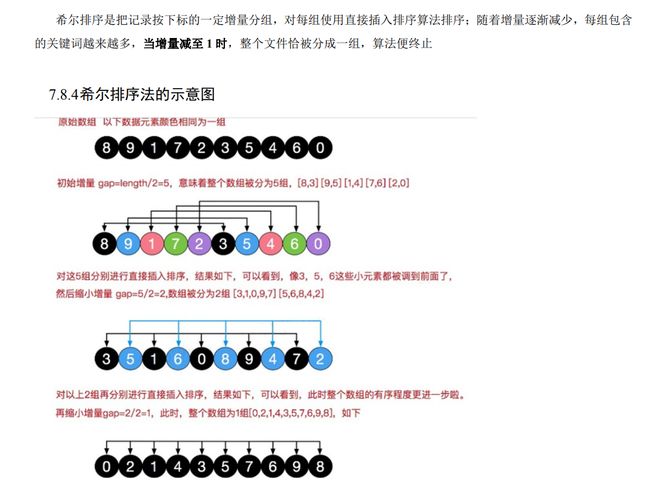
示意图
按一定增量分组,然后逐渐减小增量
初始化gap为length/2,逐渐减小为gap/2,直到gap不满足>0的条件
分组后,再对该组进行简单插入排序
- 拿图中的第三步举例,数组分成了两组[3,1,0,9,7],[5,6,8,4,2]
- 对[3,1,0,9,7]进行简单插入排序,看成前n-1个为有序数组,第n个为待插入的元素(找到自己的位置后插入即可)
不够清晰的话也可以看下边这张
代码实现
力扣912排序数组 : https://leetcode-cn。com/problems/sort-an-array/submissions/
又是这道题hhh,万能
思路概览
首先
- 我们要先初始化增量gap=length/2,然后不断缩小gap=gap/2 直到不满足gap>0
所以我们最外层会需要一个for循环来调控这个gap的变化
其次,再往内层走
- 对于分组后,由于我们是要对分组后的每一组进行简单插入排序,而插入排序我们默认从待排序数组的第二位开始,所以我们需要从每一组的第二位开始去遍历,直到整个数组的末尾
for循环让i=gap;i<数组;i++即可
最后,就对该数组进行插入排序即可
- 注意不是跟前一个进行比较了,而是跟 j-gap 比较
最初版本(for)
for的话,我是先把j赋值等于i-gap,这样的话就是跟j去比较,最后也还会去j-=gap
会导致我最后跳出循环的时候,得插到j+gap
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* sortArray(int* nums, int numsSize, int* returnSize){
//逐步缩小增量gap
for(int gap=numsSize/2;gap>0;gap=gap/2){
int insertValue = 0;
int j;
//从分组后的第一组的第二位开始
for(int i=gap;i=0的条件,这里无哨兵了
for(j=i-gap;j>=0 && insertValue 改进for
先去判断是否 j-gap>=0,满足才进循环,才会去j-=gap,所以最后j就是要插入的位置
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* sortArray(int* nums, int numsSize, int* returnSize){
//逐步缩小增量gap
for(int gap=numsSize/2;gap>0;gap=gap/2){
int insertValue = 0;
//用于插入排序中遍历待排序的数组
int j;
//从分组后的第一组的第二位开始
for(int i=gap;i=0 && insertValue 注意
- 希尔排序没有办法用到哨兵了,我们需要注意判断是否走到头了
参考
- 菜鸟教程
- 尚硅谷数据结构与算法