深度学习实战入门——CNN实现MNIST手写数字识别

今天来从头自己搭一个非常简单的卷积网络，使用的数据集是MNIST. MNIST应该算是一个被用烂了的数据集了，非常非常适合初学，数据量比较小，数据处理、训练和预测的时间都比较短，可以很好地用于把控网络搭建的整个过程。

0x01 数据和自定义函数的准备

MNIST数据集的下载地址是http://yann.lecun.com/exdb/mnist/ ，可能稍微有一点点慢，有耐心即可。一共有四个文件：

文件名	说明	大小
train-images-idx3-ubyte.gz	训练集图像	9912422 bytes
train-labels-idx1-ubyte.gz	训练集标签	28881 bytes
t10k-images-idx3-ubyte.gz	测试集图像	1648877 bytes
t10k-labels-idx1-ubyte.gz	测试集标签	4542 bytes

将它们下载到本地，不解压。

注意，MNIST数据集中的图片保存形式并不是我们经常看到的任何一种图片格式，而是以字节形式存储的。原始图像都是灰度图，标准化像素大小为20×20。通过计算像素的质心，然后平移图像以将该点定位在28×28场大小的中心，可以将图像定位在28×28图像的中心，也即我们获得的MNIST图片大小都是28*28的。

训练集包括共60000张图片，测试集共10000张图片。训练集中的手写数字来自约250人，训练集和测试集中数字的书写者是不相交的。

0x02 数据读取与图像预览

因为图片是以字节形式存储的，我们就需要把它读取到numpy array中，用于后续的训练和测试。

首先读取压缩包。图像中的灰度值是0~255范围内的，label是原始的数字标签（比如图中写的是5，它的label就是5）。深度学习中通常将tensor标准化到0-1区间内，且一般使用one-hot向量来表示样本类别，这样在后续计算正确率等的时候更加方便。所以我们提供了normalization参数选项和one_hot选项，以便将图像的灰度值标准化到0~1范围内，并将label转化为NN中常用的one-hot向量。

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import os
import gzip
from struct import unpack

train_num=60000  # 训练集样本数
test_num=10000  # 测试集样本数
img_dim=(1,28,28)  # 图像维度
img_size=784  # 28*28的图像

x_train_path=r'D:\deep_learning_pratice\mnist\train_images\train-images-idx3-ubyte.gz'
y_train_path=r'D:\deep_learning_pratice\mnist\train_labels\train-labels-idx1-ubyte.gz'
x_test_path=r'D:\deep_learning_pratice\mnist\test_images\t10k-images-idx3-ubyte.gz'
y_test_path=r'D:\deep_learning_pratice\mnist\test_labels\t10k-labels-idx1-ubyte.gz'


def read_image(path):  # 读取图像数据
    with gzip.open(path,'rb') as f:
        magic,num,rows,cols=unpack('>4I',f.read(16))
        img=np.frombuffer(f.read(),dtype=np.uint8).reshape(num,28*28)
    return img


def read_label(path):  # 读取label数据
    with gzip.open(path,'rb') as f:
        magic,num=unpack('>2I',f.read(8))
        label=np.frombuffer(f.read(),dtype=np.uint8)
    return label


def normalize_image(image):  # 图像灰度值的标准化
    img=image.astype(np.float32)/255.0
    return img


def one_hot_label(label):  # 图像标签的one-hot向量化
    lab=np.zeros((label.size,10))
    for i,row in enumerate(lab):
        row[label[i]]=1
    return lab


def load_mnist(x_train_path,y_train_path,x_test_path,y_test_path,normalize=True,one_hot=True):  # 读取mnist数据集
    '''
    Parameter
    --------
    normalize：将图像的像素值标准化到0~1区间
    one_hot：返回的label是one_hot向量

    Return
    --------
    (训练图像，训练标签)，(测试图像，测试标签)
    '''
    image={
     
        'train':read_image(x_train_path),
        'test':read_image(x_test_path)
    }

    label={
     
        'train':read_label(y_train_path),
        'test':read_label(y_test_path)
    }

    if normalize:
        for key in ('train','test'):
            image[key]=normalize_image(image[key])

    if one_hot:
        for key in ('train','test'):
            label[key]=one_hot_label(label[key])

    return (image['train'],label['train']),(image['test'],label['test'])

(x_train,y_train),(x_label,y_label)=load_mnist(x_train_path,y_train_path,x_test_path,y_test_path,normalize=True,one_hot=True)
print('Data Loads Successfully')

我们来看一下数据读取的结果：

f,ax=plt.subplots(2,2)
ax[0,0].imshow(x_train[0].reshape(28,28),cmap='Greys')  # 灰度图，reshape为28*28的像素图
ax[0,1].imshow(x_train[1].reshape(28,28),cmap='Greys')
ax[1,0].imshow(x_train[2].reshape(28,28),cmap='Greys')
ax[1,1].imshow(x_train[3].reshape(28,28),cmap='Greys')
plt.show()

看下效果：

0x03 CNN的搭建

这里我们来搭一个最简单的CNN，它包括输入层、卷积层、激励层、池化层、全连接层和输出层。首先对这几个网络层做一下说明：

输入层用于将图像数据输入到网络中；卷积层的作用是使用卷积核提取特征；激励层对卷积的线性操作增加非线性映射；池化层进行下采样，对特征图进行稀疏处理，减少数据量，提高网络训练速度；全连接层在网络末端重新拟合，减小特征损失；输出层做softmax运算，输出分类结果。

在开始之前还有一些准备工作。tensorflow的原理就像用空的tube搭一个空架子，把自己需要的东西层层堆叠在架子中，搭建的过程中架子一直是没有投入使用的。架子搭好之后，需要用时就建立新的session让架子正式投入使用，再把你的tensor送到tube里面，tensor就沿着你搭的模型架子不断流动，这一点和tensorflow的取名含义相符。

这里就会存在一个问题。虽然搭架子的时候数据并没有真的出现在架子中，但需要事先知道未来我的架子需要承受多大的tensor，类似于挑合适大小的tube来搭架子的不同位置。否则搭的架子和自己的tensor不匹配，那架子就白搭了。因此需要使用占位符对tensor的大小进行预先说明和内存预留，以便后续能够顺利地使用。

# 创建占位符
x=tf.placeholder("float",shape=[None,784])  # x是输入的图像数据维度，28*28=784，初始化为784维
y=tf.placeholder("float",shape=[None,10])  # y是图像类别的标签维度，0~9一共10个数字，初始化为10维

下面对各个层的搭建进行分别说明。输入层没啥特别的，就不单独拎出来了。

1 卷积层1

卷积的本质其实还是加权映射，卷积核就相当于一个权值矩阵，网络的训练就是要训练卷积核中的这些一个个小权值，使得通过加权求和等一系列操作之后的输出结果与真实结果更加贴近。因此，需要对卷积核中涉及到的权重和bias进行初始化。看了一些教程，发现比较普遍的初始化方法是权值随机初始化，偏置统一初始化：

# 定义卷积层1的权重和bias
w_conv1=tf.Variable(tf.truncated_normal([5,5,1,32],stddev=0.1)) # 截断生成正态分布随机数
b_conv1=tf.Variable(tf.constant(0.1,shape=[32]))  # 初始化bias，值均为0.1

然后定义卷积层1：

# 搭建卷积层1
x_image=tf.reshape(x,[-1,28,28,1])
r_conv1=tf.nn.conv2d(x_image,w_conv1,strides=[1,1,1,1],padding='SAME')+b_conv1  # 卷积操作
h_conv1=tf.nn.relu(r_conv1)  # 激活函数

这里对tf.nn.conv2d()函数做一下说明。tf.nn.conv2d()用于做图像的二维卷积，该函数的方法定义如下：

tf.nn.conv2d (input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)

其中，各参数的含义为：

input: 输入向量，输入的要做卷积的图片，要求为一个tensor，shape为[ batch, height, width, channel ]，其中batch为图片的数量，in_height 为图片高度，in_width 为图片宽度，in_channel 为图片的通道数，灰度图该值为1，彩色图为3。（也可以用其它值。原始的图片通道数只有1和3两种，但是当经过了卷积核以后，就可以有很多通道数了。比如最输入是1张图片，rgb是3通道的。第一层用10个卷积核，就是卷积10次。每一次卷积形成的都是一个二维的。10个叠加在一起。就有10个通道作为下一层的输入了）。

filter: 卷积核，要求也是一个张量，shape为 [filter_height, filter_width, in_channel, out_channels]，其中 filter_height 为卷积核高度，filter_width 为卷积核宽度，in_channel 是图像通道数 ，和 input 的 in_channel 要保持一致，out_channel 是卷积核数量。

strides: 步长，是一个一维的向量，[1, strides, strides, 1]，第一位和最后一位固定必须是1.

padding: 填充方式，可选值为“SAME” 和 “VALID”，表示的是卷积的形式，是否考虑边界。"SAME"是考虑边界，如果步长为1，得到的feature map大小就与原图大小相同（因此取名为SAME），步长为其他值时，不足的时候用0去填充周围，只会填充右侧列与下侧行；"VALID"不考虑padding, 如果不足则丢弃边缘像素，也是只会丢弃右侧列与下侧行。

函数返回卷积完成的tensor, 其维度为[batch_size, height, width, channel]这样。

通过上面的代码，我们对原始图像进行了二维卷积，卷积得到的结果加上偏置，经过relu激活函数，就可以得到卷积层1的输入h_conv1了。

tensor的维度有时候是个很难办的事情，我们来梳理一下经过卷积层1后各个tensor的维度情况（以下均不考虑batch_size这一维）：

x_image: 原始输入图像，28*28；

r_conv1: 用5*5的32个卷积核去卷x_image, padding方式为SAME，步长为1，因此输出的feature map大小与输入相同，即一共得到32个28*28的feature map.

2 池化层1

池化层的目的是进行下采样，使特征稀疏，减小数据量，加快网络的训练和预测效率。

# 搭建池化层1
h_pool1=tf.nn.max_pool(h_conv1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

这里用到的是最大池化。函数tf.nn.max_pool(input, ksize, strides, padding, name=None)的作用即为最大池化，和上面的卷积函数很类似，参数含义如下：

input: 输入要池化的向量。一般池化层都跟在卷积层后面，所以这里的输入是提取到的feature map, 也即[batch_size, height, width, channel]这样的向量。

ksize: 池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，因为不需要在batch和channels上做池化，所以这两个维度设为1.

strides: 步长，也是一个一维的向量，一般也是[1, strides, strides, 1].

padding: 同上，也是填充方式，表示是否考虑边界。

池化层的返回也是一个tensor, 维度情况为[batch_size, height, width, channel].

经过池化层后，维度情况变化为：

h_pool1: 使用2*2的池化窗口去对32个28*28的feature map进行最大池化，得到的是32个14*14的池化后的feature map.

3 卷积层2

卷积层2的目的和操作与卷积层1基本一模一样：

# 定义卷积层2的权重和bias
w_conv2=tf.Variable(tf.truncated_normal([5,5,32,64],stddev=0.1))
b_conv2=tf.Variable(tf.constant(0.1,shape=[64]))

# 搭建卷积层2
r_conv2=tf.nn.conv2d(h_pool1,w_conv2,strides=[1,1,1,1],padding='SAME')+b_conv2
h_conv2=tf.nn.relu(r_conv2)

通过卷积层2之后，各tensor的维度变化为：

h_pool1: 池化层1的输出，32个14*14的feature map；

r_conv2: 用5*5的64个卷积核去卷上一步得到的32通道feature map, padding方式依然为SAME，步长依然为1，因此输出的feature map大小也与输入相同，即一共得到64个28*28的feature map.

4 池化层2

也是与池化层1基本相同：

# 搭建池化层2
h_pool2=tf.nn.max_pool(h_conv2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')

通过池化层2之后，各tensor的维度变化为：

h_pool2: 使用2*2的池化窗口去对64个14*14的feature map进行最大池化，得到的是64个7*7的池化后的feature map.

5 全连接层

全连接层的主要目的是恢复部分损失特征，其搭建也比较简单：

# 定义全连接层的权重和bias
w_fc1=tf.Variable(tf.truncated_normal([7*7*64,1024],stddev=0.1))
b_fc1=tf.Variable(tf.constant(0.1,shape=[1024]))

# 搭建全连接层
h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64])
h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,w_fc1)+b_fc1)

因为池化层2的输出是64个7*7的feature map，因此这一步我们把每个像素点都展开，一共7*7*64个像素点。我们设置全连接层的神经元个数为1024个，因此权重w_fc1的维度定义为[7*7*64, 1024].

得到的h_pool2是二维的map，所以要将其reshape为可以输入到全连接层的tensor，也即可以与w_fc1相乘的tensor，得到h_pool2_flat.

6 输出层

输出层比较简单，在全连接层的后面添加softmax以达到分类效果即可。为了避免模型过拟合，可以再额外添加一个dropout，整体实现如下：

# 添加dropout
keep_prob=tf.placeholder(tf.float32)
h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob)

# 搭建输出层
w_fc2=tf.Variable(tf.truncated_normal([1024,10],stddev=0.1))
b_fc2=tf.Variable(tf.constant(0.1,shape=[10]))
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop,w_fc2)+b_fc2)

这里有一些新的函数，比如tf.nn.dropout()，其方法定义如下：

tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None, name=None)

各参数的含义为：

x: 输入的tensor

keep_prob: 每个元素被保留下来的概率，即设置神经元被选中的概率，float类型。在初始化时keep_prob是一个占位符, keep_prob = tf.placeholder(tf.float32) 。tensorflow在run时设置keep_prob具体的值，如keep_prob: 0.5

在tensor维度方面，全连接层的输出是[?, 1024]的tensor（这里涉及到?是在网络搭建时batch_size不确定导致的）, 且分类的总类别为10类，因此w_fc2初始化为[1024, 10]的tensor.

至此，小网络的基本架构已经搭建完毕了。

0x04 损失函数与正确率计算

我们在这里使用交叉熵损失函数和AdamOptimizer优化器来做梯度下降。此外tensorflow中还提供了很多可选择的优化器，详细信息可以参看https://blog.csdn.net/junchengberry/article/details/81102058。

# 做交叉熵
cross_entropy=-tf.reduce_sum(y*tf.log(y_conv))

# 梯度下降法
train_step=tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

# 计算正确率
correct_prediction=tf.equal(tf.argmax(y_conv,1),tf.argmax(y,1))

accuracy=tf.reduce_mean(tf.cast(correct_prediction,"float"))

这里涉及到的新函数有：

1. tf.reduce_sum(input_tensor, axis=None, keepdims=None, name=None, reduction_indices=None, keep_dims=None)，用于计算tensor沿着某一维度的和，可以在求和后降维。参数定义如下：

input_tensor：待求和的tensor

axis：指定的维，如果不指定，则计算所有元素的总和。axis是多维数组每个维度的坐标。

keepdims：是否保持原有张量的维度，设置为True，结果保持输入tensor的形状，设置为False，结果会降低维度，如果不传入这个参数，则系统默认为False

name：操作的名称

reduction_indices：在以前版本中用来指定轴，已弃用

keep_dims：在以前版本中用来设置是否保持原张量的维度，已弃用

​ axis的概念比较抽象，这里有一个讲得蛮清晰的blog: https://www.jianshu.com/p/30b40b504bae

2. tf.argmax(input,axis)，根据axis取值的不同返回每行或者每列最大值的索引。在计算正确率的时候，因为我们的输出是one-hot向量，因此每一个预测输出tensor中都会有且仅有一个元素为1. 取出预测结果y_conv中值为1的元素的下标idx_predict和真实标签y中值为1的元素的下标idx_true，并进行比较，若相等，则对于该样本的类别预测正确，不相等则预测错误。

3. tf.equal(x,y,name=None)，判断x, y 是否相等。它的判断方法不是整体判断，而是逐个元素进行判断，所以x，y 的维度要一致。它的返回是一个与x、y维度相同的tensor，其中的每个元素都是bool类型。若x[idx]==y[idx]，则返回数组correct_prediction[idx]==True, 否则return[idx]==False.

4. tf.cast(x,dtype,name=None), x是待转换的tensor, dtype是要转换到的类型，一般用于真实值和预测值比较后的布尔型转换为浮点型进行后续计算。比如：

   import tensorflow as tf
   import numpy as np
    
   y_pre = [0.9, 1.2, 0.75, 0.5, 0.8]
   y = [0.8, 1.2, 0.75, 0.9, 0.8]
   equal =  tf.equal(y_pre, y)
   cast = tf.cast(equal, 'float')
   cast1 = tf.cast(equal, dtype = float)
   cast2 = tf.cast(equal, dtype = tf.float32)
   with tf.Session() as sess:
       print(sess.run(equal))
       print(sess.run(cast))
       print(sess.run(cast1))
       print(sess.run(cast2))
   

   输出为：

   [False  True  True False  True] # equal
   [ 0.  1.  1.  0.  1.]
   [ 0.  1.  1.  0.  1.]
   [ 0.  1.  1.  0.  1.]
   

5. tf.reduce_mean(input_tensor, axis=None, keepdims=None, name=None, reduction_indices=None, keep_dims=None),与tf.reduce_sum()非常类似，用于计算张量tensor沿着指定的数轴（tensor的某一维度）上的的平均值。

0x05 CNN的训练

tensorflow通过session来激活网络模型：

def generatebatch(X,Y,n_examples, batch_size):
    for batch_i in range(n_examples // batch_size):
        start = batch_i*batch_size
        end = start + batch_size
        batch_xs = X[start:end]
        batch_ys = Y[start:end]
        yield batch_xs, batch_ys # 生成每一个batch
        
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())  # 初始化全局的varibles
    for epoch in range(10):  # 迭代10轮
        for batch_xs,batch_ys in generatebatch(x_train,y_train,60000,50):  # 这里涉及到自己定义的一个函数，用于生成一个batch的训练样本
            sess.run(train_step,feed_dict={
     x:batch_xs,y:batch_ys,keep_prob:0.5})
        if epoch % 1 ==0:
            print("Epoch {0}, accuracy: {1}".format(epoch,sess.run(accuracy,feed_dict={
     x:x_test,y:y_test,keep_prob:1.0})))

sess.run(fetches, feed_dict=None, options=None, run_metadata=None)函数用于正式激活模型并开始训练。其中fetches是我们需要从模型中“取回”的内容，只有在fetch中的图元素才会被执行。feed_dict则用于向模型中传入我们的tensor, 其中x、y是我们在模型一开始初始化的占位符，我们将生成的batch_xs、batch_ys分别传入，并设置dropout=0.5，即可开始训练。

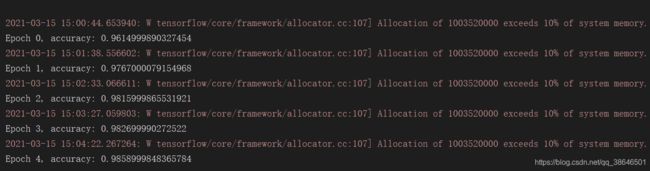
0x06 结果预览

跑了5个epoch看看结果，识别正确率在98%左右，好像还可以

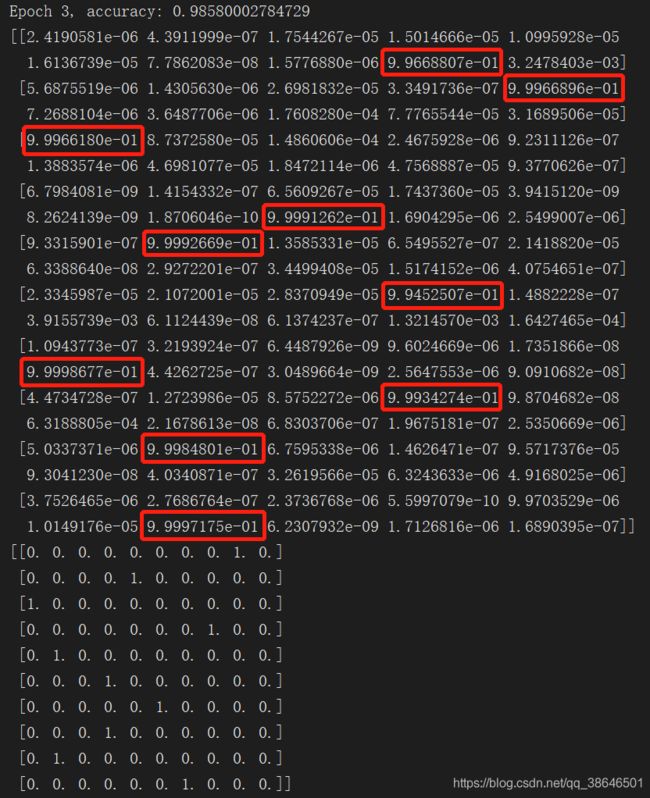
实际看一下预测的情况。在训练代码后添加最下面两句，取出预测结果y_conv和真实标签y_的前十项，y_conv输出的是类别概率，对照一下可以看出都是预测正确了的。

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(5):
        for batch_xs,batch_ys in generatebatch(x_train,y_train,60000,50):
            sess.run(train_step,feed_dict={
     x:batch_xs,y:batch_ys,keep_prob:0.5})
        if epoch % 1 ==0:
            print("Epoch {0}, accuracy: {1}".format(epoch,sess.run(accuracy,feed_dict={
     x:x_test,y:y_test,keep_prob:1.0})))
            print(sess.run(y_conv[:10],feed_dict={
     x:batch_xs,y:batch_ys,keep_prob:1.0}))
            print(sess.run(y[:10],feed_dict={
     x:batch_xs,y:batch_ys,keep_prob:1.0}))

数据集及源码：https://github.com/HoneyPotter-Gzy/CNN_mnist_practice