transformer及动手学习transformer
学习了深度学习将近一年,年初的时候便开始了transformer的学习,然而当时刚起步对于transformer一知半解,学习的是第一版《动手学深度学习》。现如今大半年已过,《动手学深度学习》也在不断更新,内容变得更加丰富充实,回过头来一次又一次的再学习transformer,每次学习都有新的收获,对于李沐老师再B站录的视频更是好评,甚至老师推出了transformer论文详解的视频,将此次重新学习归纳整理的知识记录下来,以便下一次再次重温transformer时查看又有了哪些进步。
参考:李沐老师的动手学深度学习
序言 — 动手学深度学习 2.0.0-alpha2 documentation (d2l.ai) http://zh-v2.d2l.ai/chapter_preface/index.html
http://zh-v2.d2l.ai/chapter_preface/index.html
跟李沐学AI的个人空间_哔哩哔哩_bilibili https://space.bilibili.com/1567748478/dynamic
https://space.bilibili.com/1567748478/dynamic
RNN网络Pytorch详解:上一篇博客循环神经网络(RNN、LSTM、GRU)以及Pytorch的使用
注意力机制
卷积、全连接、池化层只考虑不随意线索
注意力机制则显示的考虑随意线索
随意线索被称之为查询(query)
每个输入是一个值(value)和不随意线索(key)的对,可以相等也可以不相等
通过注意力池化层来有偏向性的选择某些输入
非参注意力池化层
![]()
参数化的注意力机制
注意力机制中,通过query(随意线索)和key(不随意线索)来有偏向性的选择输入
注意力机制拓展到高维度
假设query ![]() , m对key-value(
, m对key-value(![]() ) ......,其中
) ......,其中![]() ,三者维度均可以不同
,三者维度均可以不同
- 先计算q和k的注意力分数
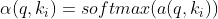
- 再加权计算
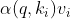 注意力机制向量
注意力机制向量
Additive Attention
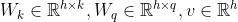 ,
, 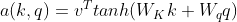
- 等价于将query和key合并起来后放入到一个隐藏层大小为h输出大小为1的单隐藏层MLP
Scaled Dot-Product Attention
如果query和key都是同样的长度![]() , 则
, 则![]()
向量化版本
![]() ,表示有n个query,m个key-value对, 向量长度均不相等
,表示有n个query,m个key-value对, 向量长度均不相等
- 注意力分数:
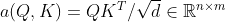
- 注意力池化:
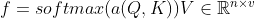
总结
注意力分数是query和key的相似度,注意力权重是分数的softmax结果
两种常见的分数计算
- 将query和key合并起来进入一个单输出单隐藏层的MLP
- 直接将query和key做内积
注意力机制代码实现
Pytorch中的masked_fill()函数
masked_fill()函数主要用在transformer的attention机制中,在时序任务中,主要是用来mask掉由于padding使得每批batch中填充的元素。此时mask主要实现时序上的mask。
import torch
a = torch.tensor([1, 0, 2, 3])
b = a.masked_fill(mask = torch.ByteTensor([0, 0, 1, 1]), value = torch.tensor(-100))
print(b)
# tensor([ 1, 0, -100, -100])其中mask必须是一个ByteTensor,shape必须和a相同,是将mask中为1的元素所在的索引,替换为value中的值。
Pytorch中的contiguous()函数
contiguous函数:返回一个内存连续的tensor,如果原tensor内存连续,则返回原tensor。
contiguous一般与transpose,permute,view搭配使用:使用transpose或permute进行维度变换后,调用contiguous,然后方可使用view对维度进行变形。
- transpose、permute等维度变换操作后,tensor在内存中不再是连续存储的,而view操作要求tensor的内存连续存储,所以需要contiguous来返回一个contiguous copy。
- 维度变换后的变量是之前变量的浅拷贝,指向同一区域,即view操作会连带原来的变量一同变形,这是不合法的,所以也会报错,也即contiguous返回了tensor的深拷贝contiguous copy数据。
在pytorch中,只有很少几个操作是不改变tensor的内容本身,而只是重新定义下标与元素的对应关系。换句话说,这种操作不进行数据拷贝和数据的改变,变的是元数据,这些操作是
- narrow() 切片功能 x.narrow(dim, start, length) 在dim维度上,截取从start - start + lenth 长度的切片
- view() 重构张量
- expand() 扩展张量 y = x.expand(a, b) 将张量扩展为 a * b 倍
- transpose() 交换矩阵维度 torch.transpose(x, 1, 0, 2) 将0维度和1维度转换
注意力机制代码实现
实现点积相乘注意力机制
注意力机制分数
class AttentionScore(nn.Module):
"""
correlation_func = 1, sij = x1^Tx2
correlation_func = 2, sij = (Wx1)D(Wx2)
correlation_func = 3, sij = Relu(Wx1)DRelu(Wx2)
"""
#hidden_size represents the dimension of the query vector and the key vector
def __init__(self, input_size, hidden_size, correlation_func=1, do_similarity=False):
super(AttentionScore, self).__init__()
self.correlation_func = correlation_func
self.hidden_size = hidden_size
self.dropout = nn.Dropout(0.1)
if correlation_func == 2 or correlation_func == 3:
self.linear = nn.Linear(input_size, hidden_size, bias=False)
if do_similarity:
self.diagonal = nn.Parameter(torch.ones(1, 1, 1) / (hidden_size ** 0.5), requires_grad=False)
else:
self.diagonal = nn.Parameter(torch.ones(1, 1, hidden_size), requires_grad=True)
def forward(self, x1, x2):
'''
Input:
x1: batch x word_num1 x dim (query)
x2: batch x word_num2 x dim (key)
Output: (Scores between query and key)
scores: batch x word_num1 x word_num2
'''
x1_rep = x1
x2_rep = x2
batch = x1_rep.size(0)
word_num1 = x1_rep.size(1)
word_num2 = x2_rep.size(1)
dim = x1_rep.size(2)
if self.correlation_func == 2 or self.correlation_func == 3:
x1_rep = self.linear(x1_rep.contiguous().view(-1, dim)).view(batch, word_num1, self.hidden_size) # Wx1
x2_rep = self.linear(x2_rep.contiguous().view(-1, dim)).view(batch, word_num2, self.hidden_size) # Wx2
if self.correlation_func == 3:
x1_rep = F.relu(x1_rep)
x2_rep = F.relu(x2_rep)
x1_rep = x1_rep * self.diagonal.expand_as(x1_rep)
# x1_rep is (Wx1)D or Relu(Wx1)D
# x1_rep: batch x word_num1 x dim (corr=1) or hidden_size (corr=2,3)
scores = torch.bmm(x1_rep, x2_rep.transpose(1, 2)) / math.sqrt(dim)
# scores = x1_rep.bmm(x2_rep.transpose(1, 2))
return scores注意力机制代码
class Attention(nn.Module):
def __init__(self, input_size, hidden_size, correlation_func=1, do_similarity=False):
super(Attention, self).__init__()
self.scoring = AttentionScore(input_size, hidden_size, correlation_func, do_similarity)
self.dropout = nn.Dropout(dropout)
def forward(self, x1, x2, x2_mask, x3=None, drop_diagonal=False):
'''
For each word in x1, get its attended linear combination of x3 (if none, x2),
using scores calculated between x1 and x2.
Input:
x1: batch x word_num1 x dim (query)
x2: batch x word_num2 x dim (key)
x2_mask: batch x word_num2
x3 (if not None) : batch x word_num2 x dim_3 (value)
Output:
attended: batch x word_num1 x dim_3
'''
batch = x1.size(0)
word_num1 = x1.size(1)
word_num2 = x2.size(1)
if x3 is None:
x3 = x2
scores = self.scoring(x1, x2)
# scores: batch x word_num1 x word_num2
empty_mask = x2_mask.eq(0).unsqueeze(1).expand_as(scores)
scores.data.masked_fill_(empty_mask.data, -100) #Set the partial score of padding to 0
if drop_diagonal:
assert (scores.size(1) == scores.size(2))
diag_mask = torch.diag(scores.data.new(scores.size(1)).zero_() + 1).byte().unsqueeze(0).expand_as(scores)
scores.data.masked_fill_(diag_mask, -float('inf'))
# softmax
alpha_flat = F.softmax(scores.view(-1, x2.size(1)), dim=1)
alpha = alpha_flat.view(-1, x1.size(1), x2.size(1))
# alpha: batch x word_num1 x word_num2
attended = torch.bmm(self.dropout(alpha), x3)
# attended = alpha.bmm(x3)
# attended: batch x word_num1 x dim_3
return attended序列到序列学习(seq2seq)
Seq2seq从一个句子生成另一个句子,将编码器最后时间隐状态来初始解码器隐状态完成信息传递
- 编码器是一个RNN,读取输入句子(可以是双向)
- 解码器使用另外一个RNN输出
衡量生成序列的好坏的BLEU
![]() 是预测中所有n-gram的精度
是预测中所有n-gram的精度
example:标签序列ABCDEF和预测序列ABBCD,有![]()
seq2seq中通过隐状态在编码器和解码器中传递信息
注意力机制可以根据解码器RNN的输出来匹配到合适的编码器RNN的输出来更有效地传递信息
编码器将长度可变的输入序列转换成形状固定的上下文变量c,我们使用另一个循环神经网络作为解码器,将来自上一时间步的输出和上下文变量c作为其输入, 然后在当前时间步将它们和上一隐藏状态![]() 转换为隐藏状态
转换为隐藏状态![]() 。
。
实现解码器时,我们直接使用编码器最后一个时间步的隐藏状态来初始化解码器的隐藏状态。要求使用循环神经网络实现的编码器和解码器具有相同数量的层和隐藏单元。为了进一步包含经过编码的输入序列的信息,上下文变量在所有的时间步与解码器的输入进行拼接(concatenate)。为了预测输出词元的概率分布,在循环神经网络解码器的最后一层使用全连接层来变换隐藏状态。
Pytorch代码实现Encoder和Decoder
import collections
import math
import torch
from torch import nn
class Seq2SeqEncoder(nn.Module):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, dropout = 0):
super(Seq2SeqEncoder, self).__init__()
#嵌入层
self.embedding = nn.Embedding(vocab_size, embed_size)
#第一个参数表示词表大小,第二个参数表示一个符号的维度, 第三个参数表示用0填充的符号在词表中的位置
self.rnn = nn.GRU(embed_size, num_hiddens, num_layers, dropout = dropout)
def forward(self, X, *args):
#输出'X'的形状:(batch_size, num_steps, embed_size)
#(行数等于输入词表的大小vocab_size,列数等于特征向量的维度embed_size)
X = self.embedding(X)
#在循环神经网络模型中,第一个轴对应于时间步
X = X.permute(1, 0, 2)
output, state = self.rnn(X)
#output的形状:(num_steps, batch_size, num_hiddens)
#state[0]的形状:(num_layers, batch_size, num_hiddens)
return output, state
#验证编码器
encoder = Seq2SeqEncoder(vocab_size = 10, embed_size = 8, num_hiddens = 16, num_layers = 2)
encoder.eval()
X = torch.zeros((4, 9), dtype = torch.long)
output, state = encoder(X)
print(output.shape)#torch.Size([9, 4, 16])
print(state.shape)#torch.Size([2, 4, 16])
class Seq2SeqDecoder(nn.Module):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, dropout = 0):
super(Seq2SeqDecoder, self).__init__()
#嵌入层
self.embedding = nn.Embedding(vocab_size, embed_size)
#RNN的输入是 编码器隐藏状态维度和解码器输入维度拼接
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers, dropout = dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs):
return enc_outputs[1]
def forward(self, X, state):
#输出'X'的形状:(batch_size, num_steps, embed_size)
X = self.embedding(X).permute(1, 0, 2)
context = state[-1].repeat(X.shape[0], 1, 1)#(9, 4, 16)
X_and_context = torch.cat((X, context), 2)#(9, 4, 24)
output, state = self.rnn(X_and_context, state)#(9, 4, 16), (2, 4, 16)
output = self.dense(output).permute(1, 0, 2)#(4, 9, 10)
return output, state
#验证解码器
decoder = Seq2SeqDecoder(vocab_size = 10, embed_size = 8, num_hiddens = 16, num_layers = 2)
decoder.eval()
state = decoder.init_state(encoder(X))
print(state.shape)#torch.Size([2, 4, 16])
output, state = decoder(X, state)
print(output.shape)#torch.Size([4, 9, 10]
print(state.shape)#torch.Size([2, 4, 10]
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X):
enc_outputs = self.encoder(enc_X)
dec_state = self.decoder.init_state(enc_outputs)
return self.decoder(dec_X, dec_state)加上注意力机制的Decoder
新的基于注意力的模型与Seq2Seq中的模型相同。基于注意力模型的上下文变量c在任何解码时间步骤![]() 都会被
都会被![]() 替换。假设输入序列中有T个词元,解码时间步长
替换。假设输入序列中有T个词元,解码时间步长![]() 的上下文变量是注意力的输出:
的上下文变量是注意力的输出:
其中,时间步![]() 时的解码器隐藏状态
时的解码器隐藏状态![]() 是查询,编码器隐藏状态
是查询,编码器隐藏状态![]() 既是键,也是值,注意力权重
既是键,也是值,注意力权重![]() 时使用定义的加性注意力打分函数计算的。
时使用定义的加性注意力打分函数计算的。
初始化解码器的状态
- 编码器在所有时间步的最终隐层状态(作为注意力的键和值)
- 最后一个时间步的编码器全层隐藏状态(初始化解码器的隐藏状态)
- 编码器的有效长度(排除在注意力池中填充词元)
在每个解码时间步骤中,解码器上一个时间步的最终层隐藏状态将用作关注的查询。因此,注意力输出和输入嵌入都连接为循环神经网络解码器的输入。
实现Decoder中的加性注意力机制AdditiveAttention
- 初始化:key的维度、query的维度、隐藏层的维度([批量大小、序列步长、特征维度])
- 输入:query(bs, q_number, q_vector)、key(bs, k_number, k_vector)、value(bs, v_number, v_vecotr)
- 输出:每个查询 关于所有键对应的值 的加权和,即查询关于所有键的注意力值(batch, q_number, v_vector)
加性注意力机制代码AdditiveAttention
import collections
import math
import torch
from torch import nn
import numpy as np
def sequence_mask(X, valid_len, value = 0):
maxlen = X.size(1)
mask = torch.arange((maxlen), dtype = torch.float32, device = X.device)[None, :] < valid_len[:, None]
#mask = tensor([[ True, False, False],
# [ True, True, False]])
X[~mask] = value
return X
def masked_softmax(X, valid_lens):
"""通过在最后一个轴上遮蔽元素来执行 softmax 操作"""
# `X`: 3D张量, `valid_lens`: 1D或2D 张量
if valid_lens is None:
return nn.functional.softmax(X, dim=-1)
else:
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# 在最后的轴上,被遮蔽的元素使用一个非常大的负值替换,从而其 softmax (指数)输出为 0
X = sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
value=-1e6)
return nn.functional.softmax(X.reshape(shape), dim=-1)
#加性注意力(当查询和键是不同长度的矢量时,可以使用加性注意力作为评分函数)
#通过使用tanh作为激活函数,并且禁用偏置项
class AdditiveAttention(nn.Module):
#加性注意力
def __init__(self, key_size, query_size, num_hiddens, dropout):
super(AdditiveAttention, self).__init__()
self.W_k = nn.Linear(key_size, num_hiddens, bias = False)
self.W_q = nn.Linear(query_size, num_hiddens, bias = False)
self.w_v = nn.Linear(num_hiddens, 1, bias = False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
#queries的形状:(batch_size, 查询的个数, 1, num_hidden)
#key的形状:(batch_size, 1, "键-值"对的个数, num_hidden)
#使用广播方式进行求和
features = queries.unsqueeze(2) + keys.unsqueeze(1)
features = torch.tanh(features)
#score的形状:(batch, 查询的个数, 键值对的个数)
scores = self.w_v(features).squeeze(-1)
self.attention_weights = masked_softmax(scores, valid_lens)
#values的形状:(batch, 键值对的个数, 值的维度)
return torch.bmm(self.dropout(self.attention_weights), values)
#返回值为 每个查询值关于所有键的注意力所形成的 值的加权和
#验证注意力机制代码
#torch.normal(mean, std, size)该函数返回从单独的正态分布中提取的随机数的张量,该正态分布的均值是mean,标准差是std。
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
values = torch.arange(40, dtype = torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)
valid_lens = torch.tensor([2, 6])
#查询、键、值的形状为(批量大小、步数或词元序列长度、特征大小)
print(queries.shape)#torch.Size([2, 1, 20])
print(keys.shape)#torch.Size([2, 10, 2]) key的步数为10, 特征维度为2
print(values.shape)#torch.Size([2, 10, 4]) value的步数为10, 特征维度为4
print(valid_lens.shape)#torch.Size([2])
attention = AdditiveAttention(key_size = 2, query_size = 20, num_hiddens = 8, dropout = 0.1)
attention.eval()
output = attention(queries, keys, values, valid_lens)
print(output.shape)#torch.Size([2, 1, 4]添加注意力机制的Seq2Seq,代码实现Seq2SeqAttentionDecoder
#加上注意力机制的解码器
class Seq2SeqAttentionDecoder(nn.Module):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, dropout = 0):
super(Seq2SeqAttentionDecoder, self).__init__()
#AdditiveAttention的参数分别为:key的维度, query的维度, 隐藏层的维度
self.attention = AdditiveAttention(num_hiddens, num_hiddens, num_hiddens, dropout)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers, dropout = dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens):
outputs, hidden_state = enc_outputs
return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)
def forward(self, X, state):
#enc_outputs的形状(batch_size, num_steps, num_hiddens) #编码器的输出
#hidden_state的形状(num_layers, batch_size, num_hiddens) #编码器隐藏状态
#embed_size = None, 表示未padding的个数
enc_outputs, hidden_state, enc_valid_lens = state
#输出X的形状为(num_steps, batch_size, embed_size)
X = self.embedding(X).permute(1, 0, 2)#维度(序列长度、批次大小、每个符号的特征维度) #解码器的输入
outputs, self._attention_weights = [], [] #保存query和key的分数矩阵
#按序列遍历
for x in X:
#query的形状为(batch_size, 1, num_hiddens), 上一时间步的隐藏状态相当于query
query = torch.unsqueeze(hidden_state[-1], dim = 1)
#context的形状为(batch_size, 1, num_hiddens) 表示上一步隐藏状态和编码器所有序列输出的注意力的值
#torch.Size([4, 1, 16]) torch.Size([4, 7, 16]) torch.Size([4, 7, 16])-->torch.Size([4, 1, 16])(恰好query、key、value的维度均为隐藏维度)
context = self.attention(query, enc_outputs, enc_outputs, enc_valid_lens)
# 在特征维度上连结, x变形为(1, batch_size, embed_size + num_hiddens)
x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1) #表示 注意力的值和解码器的输入作为RNN网络当前时间步输入
#out为当前时间步的输出([1, batch_size, num_hiddens]), hidden_state为当前时间步的隐藏状态([num_layers, batch_size, num_hiddens])
out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
outputs.append(out) #每一时间步解码器的输出
self._attention_weights.append(self.attention.attention_weights) #表示每一时间步query和key的分数矩阵
# 全连接层变换后, `outputs`的形状为
# (`num_steps`, `batch_size`, `vocab_size`)
outputs = self.dense(torch.cat(outputs, dim=0))
outputs = outputs.permute(1, 0, 2)
#返回
#output 解码器的输出 #torch.Size([4, 7, 10])
#enc_outputs 编码器所有时间步的隐藏状态 #torch.Size([4, 7, 16])
#hidden_state 解码器最后一个时间步的隐藏状态 #torch.Size([2, 4, 16])
#enc_valid_lens 整体输入有效的长度, None
return outputs, [enc_outputs, hidden_state, enc_valid_lens]
#使用包含7个时间步的4个序列输入的小批量测试 注意力解码器
encoder = Seq2SeqEncoder(vocab_size = 10, embed_size = 8, num_hiddens = 16, num_layers = 2)
encoder.eval()
decoder = Seq2SeqAttentionDecoder(vocab_size = 10, embed_size = 8, num_hiddens = 16, num_layers = 2)
decoder.eval()
X = torch.zeros((4, 7), dtype = torch.long)#(batch_size, num_steps)
state = decoder.init_state(encoder(X), None)#编码器两个输出, (所有时间步的输出,最后一个时间步的全层隐藏状态)
print(state[0].shape)#torch.Size([4, 7, 16]) 编码器在所有时间步的输出
print(state[1].shape)#torch.Size([2, 4, 16]) 编码器最后一个时间步的全层隐藏状态
print(state[2])#None 编码器全部为有效长度
output, state = decoder(X, state)
print(output.shape) #torch.Size([4, 7, 10])
print(len(state)) #3
print(state[0].shape) #torch.Size([4, 7, 16])
print(state[1].shape) #torch.Size([2, 4, 16])损失函数
对于语言模型,特定的填充词元被添加到序列的末尾,因此不同长度的序列可以以相同形状的小批量加载。但是,应该将填充词元的预测排除在损失函数的计算之外。例如:如果两个序列的有效长度(不包括填充词元)分别为1和2,则第一个序列的第一项和第二个序列的前两项之后的剩余项将被清除为零。
损失函数的具体实现原理,还需要进一步探索
损失函数代码实现
def sequence_mask(X, valid_len, value = 0):
maxlen = X.size(1)
mask = torch.arange((maxlen), dtype = torch.float32, device = X.device)[None, :] < valid_len[:, None]
#mask = tensor([[ True, False, False],
# [ True, True, False]])
X[~mask] = value
return X
X = torch.tensor([[1, 2, 3], [4, 5, 6]])
sequence_mask(X, torch.tensor([1, 2]))
X = torch.ones(2, 3, 4)
sequence_mask(X, torch.tensor([1, 2]), value = -1)
#我们可以通过扩展softmax交叉熵损失函数来这遮蔽不相关的预测。最初,所有预测词元的掩码都设置为1。
#一旦给定了有效长度,与填充词元对应的掩码将被设置为0.最后,将所有词元的损失乘以掩码,以过滤掉损失中填充词元产生的不相关预测
class MaskedSoftmaxCELoss(nn.CrossEntropyLoss):
#带遮蔽的softmax交叉熵损失函数
#pred形状:(batch_size, num_steps, vocab_size)
#label形状:(batch_size, num_steps)
#valid_len形状:(batch_size)
def forward(self, pred, label, valid_len):
weights = torch.ones_like(label)
weights = sequence_mask(weights, valid_len)
self.reduction = 'none'
unweighted_loss = super(MaskedSoftmaxCELoss, self).forward(pred.permute(0, 2, 1), label)
weighted_loss = (unweighted_loss * weights).mean(dim = 1)
return weighted_loss
loss = MaskedSoftmaxCELoss()
loss(torch.ones(3, 4, 10), torch.ones((3, 4), dtype = torch.long), torch.tensor([4, 2, 0]))自注意力
给定序列![]()
自注意力池化层将![]() 当作key,value, query来对序列抽取特征得到
当作key,value, query来对序列抽取特征得到![]()
其中,![]() , 每个序列单元既当key,又当value,又当query。
, 每个序列单元既当key,又当value,又当query。
位置编码
位置编码矩阵
class PositionalEncoding(nn.Module):
def __init__(self, num_hiddens, dropout, max_len = 1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
#创建一个足够长的'P'
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype = torch.float32).reshape(-1, 1) / torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)绝对位置信息
绝对位置信息矩阵,通过在序列上进行频率变换
相对位置信息
位置于![]() 处的位置编码可以线性投影位置
处的位置编码可以线性投影位置![]() 处的位置编码来表示, 投影矩阵与
处的位置编码来表示, 投影矩阵与![]() 无关。
无关。
记![]()
![]()
备注
位置编码中的位置在实际中指的是一个序列中输入的位置![]() 。对于下一个句子,每个样本不同的位置添加相同的东西。即位置编码每个位置添加的东西是相同的。
。对于下一个句子,每个样本不同的位置添加相同的东西。即位置编码每个位置添加的东西是相同的。
位置编码不需要模型自动学习,位置编码是生成的。
位置编码初始化之后,变成nn.parameter这种形式即可。
总结
- 自注意力池化层将
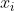 当作key, value, query来对序列抽取特征
当作key, value, query来对序列抽取特征 - 完全并行,最长序列为1,但对长序列计算复杂度高
- 位置编码在输入中加入位置信息,使得自注意力能够记忆位置信息
Transformer
- 基于编码器-解码器架构来处理序列对
- 跟使用注意力的seq2seq不同,Transformer是纯基于注意力
多头注意力
在实践中,当给定相同的查询、键和值的集合时,我们希望模型可以基于相同的注意力机制学习到不同的行为,然后将不同的行为作为知识组合起来,例如捕获序列内各种范围的依赖关系。因此,允许注意力机制组合使用查询、键和值的不同子空间表示(representation subspaces)可能是有益的。
与使用单独一个注意力汇聚不同,我们可以用独立学习得到的h组不同的线性投影(linear projections)来变换查询、键和值,然后将这h组变换后的查询、键和值并行地送到注意力汇聚中。最后,将这h个注意力汇聚输出拼接在一起,并且通过另一个可以学习的线性投影进行变换,以产生最终输出。该种设计被称为多头注意力,其中h个注意力汇聚输出中的每一个输出都被称作一个头(head)。
多头注意力机制是使用了多个注意力机制,使得每个注意力机制关注不同的地方,类似于卷积神经网络中的多通道。多头注意力融合了来自于相同的注意力汇聚产生的不同的知识,这些知识的不同来源于相同的查询、键和值的不同的子空间表示。基于适当的张量操作,可以实现多头注意力的并行计算。
- 对同一key,value,query,希望抽取不同的信息。例如短距离关系和长距离关系
- 多头注意力使用h个独立的注意力池化。合并各个头(head)输出得到最终输出
公式推导:
- query
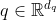 , key
, key 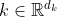 , value
, value 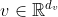
- 头 i 的可学习参数
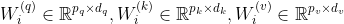
- 头 i 的输出
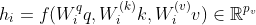 , (f是一个注意力机制函数)
, (f是一个注意力机制函数) - 输出的可学习参数
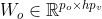
- 多头注意力的输出
![W_{o} [h_{1} ... h_{h}]^{T} \in \mathbb{R}^{p_{o}}](http://img.e-com-net.com/image/info8/4303ff6d43fa44e78a67e84df07cd397.gif)
有掩码的多头注意力
- 解码器对于序列中一个元素输出时,不应该考虑该元素之后的元素
- 可以通过掩码来实现,即计算
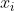 输出时,假装当前序列长度为
输出时,假装当前序列长度为
基于位置的前馈网络
- 将输入形状由(b, n, d)变换成(bn, d) b是batch_size, n序列的长度, d是特征
- 作用两个全连接层
- 输出形状由(bn, d)变化回(b, n, d)
- 等价于两层核窗口为1的一维卷积层
层归一化
- 批量归一化对每个特征/通道里元素进行归一化(不适合序列长度会变的NLP应用)
- 层归一化对每个样本里的元素进行归一化
信息传递
- 编码器中的输出
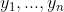
- 将其作为解码中第 i 个Transformer块中多头注意力的key和value(它的query来自目标序列)
- 意味着编码器和解码器中块的个数和输出维度都是一样的
预测
- 预测第t+1个输出时
- 解码器中输入前t个预测值(在自注意力中,前t个预测值作为key和value, 第t个预测值还作为query)
总结
- Transformer是一个纯使用注意力的编码-解码器
- 编码器和解码器都有n个transformer块
- 每个块里使用多头(自)注意力,基于位置的前馈网络,和层归一化
关于Transformer的几个内部细节的总结
关于Transformer几个内部细节的总结 - 知乎
关于Transformer几个内部细节的总结 - 知乎
import math
import torch
from torch import nn
#为了使得多个头并行计算,MultiHeadAttention类使用了两个转置函数
#transpose_output函数反转了transpose_qkv函数的操作
def transpose_qkv(X, num_heads):
#输入X的形状:(batch_size, 键值对的个数, num_hiddens)
#输出X的形状:(batch_size, 键值对的个数, num_heads, num_hiddens / num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
#输出X的形状:(batch_size, num_heads, 键值对的个数, num_hiddens / num_heads)
X = X.permute(0, 2, 1, 3)
#output的形状:(batch_size * num_head, 键值对的个数,num_hiddens / num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
def tranpose_output(X, num_heads):
#输入X的形状:(batch_size, 键值对的个数, num_heads, num_hiddens / num_heads)
#输出X的形状:(batch_size, 键值对的个数,num_hiddens)
#逆转 transpose_qkv 函数的操作
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
#注意力机制
def sequence_mask(X, valid_len, value = 0):
maxlen = X.size(1)
mask = torch.arange((maxlen), dtype = torch.float32, device = X.device)[None, :] < valid_len[:, None]
#mask = tensor([[ True, False, False],
# [ True, True, False]])
X[~mask] = value
return X
def masked_softmax(X, valid_lens):
"""通过在最后一个轴上遮蔽元素来执行 softmax 操作"""
# `X`: 3D张量, `valid_lens`: 1D或2D 张量
if valid_lens is None:
return nn.functional.softmax(X, dim=-1)
else:
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# 在最后的轴上,被遮蔽的元素使用一个非常大的负值替换,从而其 softmax (指数)输出为 0
X = sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
value=-1e6)
return nn.functional.softmax(X.reshape(shape), dim=-1)
class DotProductAttention(nn.Module):
"""缩放点积注意力"""
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
# `queries` 的形状:(`batch_size`, 查询的个数, `d`)
# `keys` 的形状:(`batch_size`, “键-值”对的个数, `d`)
# `values` 的形状:(`batch_size`, “键-值”对的个数, 值的维度)
# `valid_lens` 的形状: (`batch_size`,) 或者 (`batch_size`, 查询的个数)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
# 设置 `transpose_b=True` 为了交换 `keys` 的最后两个维度
scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
# pq = pk = pv = po/ho
# pq h = pk h = pv h = po, 则可以并行计算h个头, po是通过num_hiddens指定的
class MultiHeadAttention(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens, num_heads, dropout, bias = False):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.attention = DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias = bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias = bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias = bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias = bias)
def forward(self, queries, keys, values, valid_lens):
#queries, keys, values的形状:(batch_size, 键值对的个数, num_hiddens)
#valid_lens的形状:(batch_size, 查询的个数)
#经过变换后,输出的queries, keys, values的形状:(batch_size * num_heads, 键值对的个数, num_hiddens / num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
#在轴0, 将第一项(标量或者矢量)复制num_heads次
valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim = 0)
#output的形状:(batch_size * num_heads, 键值对的个数, num_hiddens / num_heads)
output = self.attention(queries, keys, values, valid_lens)
#output_concat的形状:(batch_size, 键值对的个数, num_hiddens)
output_concat = tranpose_output(output, self.num_heads)
return self.W_o(output_concat)
#使用键和值相同的例子测试MultiHeadAttention类。多头注意力输出的形状(batch_size, num_queries, num_hiddens)
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens, num_hiddens, num_heads, 0.5)
attention.eval()
batch_size, num_queries, num_kvpairs, valid_lens = 2, 4, 6, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
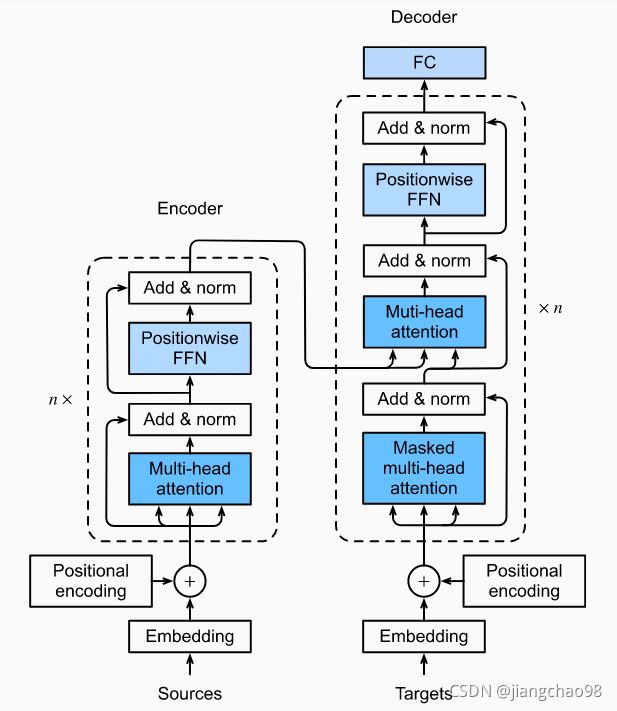
print(attention(X, Y, Y, valid_lens).shape)Transformer架构
Transformer是由编码器和解码器组成的。Transformer的编码器和解码器是基于自注意力的模块叠加而成的,输入序列和目标序列的嵌入(embedding)表示加上位置编码(positional encoding),再分别输入到编码器和解码器中。
Transformer的编码器是由多个相同的层叠加而成的,每个层都有两个子层。第一个子层是多头自注意力(multi-head self-attention)汇聚;第二个子层是基于位置的前馈网络(positionwise feed-forward network)。具体而言,在计算编码器的自注意力时,查询、键和值都来自前一个编码器层的输出,每个子层都采用了残差连接。在Transformer中,对于序列中任何位置的任何输入![]() 都要求满足
都要求满足![]() ,以便残差连接满足
,以便残差连接满足![]() ,紧接应用层归一化。因此,输入序列对应的每个位置,Transformer编码器都将输出一个
,紧接应用层归一化。因此,输入序列对应的每个位置,Transformer编码器都将输出一个![]() 维表示向量。
维表示向量。
Transformer的解码器也是由多个相同的层叠加而成的,解码器还添加了第三个子层,称为编码器-解码器注意力(encoder-decoder attention)层。在编码器-解码器注意力中,查询来自前一个解码器层的输出,而键和值来自整个编码器的输出。在解码器自注意力中,查询、键和值都来自上一个解码器层的输出。但是,解码器中的每个位置只能考虑该位置之前的所有位置。这种遮蔽(masked)注意力保留了自回归(auto-regressive)属性,确保预测仅依赖于已生成的输出词元。
- Transformer中的残差连接和层归一化是训练非常深度的模型的重要工具
基于位置的前馈网络
Transformer模型中基于位置的前馈网络使用同一个多层感知机(MLP),作用是对所有的序列位置的表示进行转换。因为同一个多层感知机对所有位置上的输入进行变换,所以当所有这些位置的输入相同时,它们的输出也是相同的。
class PositionWiseFFN(nn.Module):
def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs):
super(PositionWiseFFN, self).__init__()
self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
self.relu = nn.ReLU()
self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)
def forward(self, X):
return self.dense2(self.relu(self.dense1(X)))
ffn = PositionWiseFFN(4, 4, 8)
ffn.eval()
out = ffn(torch.ones((2, 3, 4)))
print(out.shape)
print(out[0])
#
torch.Size([2, 3, 8])
tensor([[-0.1430, -0.1947, -0.4596, 0.0166, 0.1469, -0.0031, 0.0553, -0.2613],
[-0.1430, -0.1947, -0.4596, 0.0166, 0.1469, -0.0031, 0.0553, -0.2613],
[-0.1430, -0.1947, -0.4596, 0.0166, 0.1469, -0.0031, 0.0553, -0.2613]],
grad_fn=) 残差连接和层归一化
加法和归一化(add&norm)组件,是由残差连接和紧随其后的层归一化组成的。两者都是构建有效的深度结构的关键。
class AddNorm(nn.Module):
def __init__(self, normalized_shape, dropout):
super(AddNorm, self).__init__()
self.dropout = nn.Dropout(dropout)
#layernorm中的normalized_shape 是算矩阵中的后面几维
self.ln = nn.LayerNorm(normalized_shape)
def forward(self, X, Y):
return self.ln(self.dropout(Y) + X)
#残差连接要求两个输入的形状相同,以便加法操作后输出张量的形状相同
add_norm = AddNorm([3, 4], 0.5)
add_norm.eval()
add_norm(torch.ones((2, 3, 4)), torch.ones((2, 3, 4))).shape10.7. Transformer — 动手学深度学习 2.0.0-alpha2 documentation (d2l.ai)
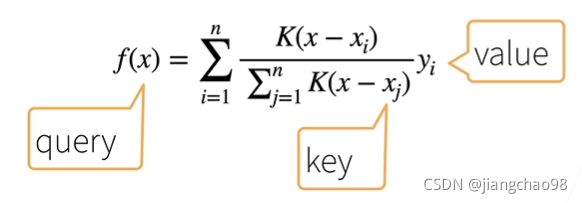
![exp \left ( min \left [ 0, 1 - \frac{len_{label}}{len_{pred}} \right ] \right ) \prod_{n=1}^{k}p_{n}^{1 / 2^{n}}](http://img.e-com-net.com/image/info8/d537dd4bee4544fe80c4dc07f9c9ffa2.gif)