机器学习基础学习-在逻辑回归中使用多项式特征
前言
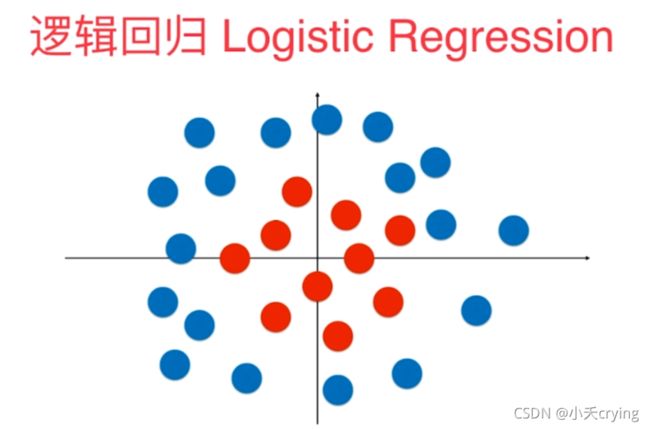
在之前的博客中讲到的逻辑回归,其实本质是在平面上找一条直线,用这条直线来分割所有样本对应的分类。所以之前说逻辑回归在绝大多数情况下,只能解决二分类问题,因为这个直线只能将我们的平面分成两个部分。但即使如此,我们会发现直线这种分类方式太过于简单了,有很多其他情况不能单纯通过直线来分类,比如下图,在我们的特征平面中分布着一些样本点,红色属于一类,蓝色属于另一类,对于这些样本点来说,我们不能通过直线将他们分成两部分,因为这些样本点的分布是非线性的分布。
一、在逻辑回归中使用多项式特征基本思路
其实通过观察我们可以看到这些样本点其实可以通过一个圆形的决策边界把他们分割成两部分。但我们之前实现的方法是没有办法得到这样一个圆形的决策边界。
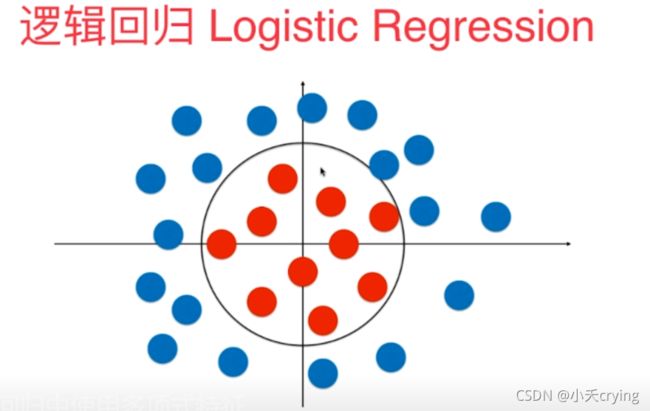
一般圆的方程如下图是
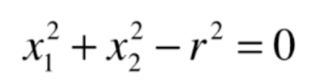
接下来我们的想法就是是否能让我们的逻辑回归学习到这样的边界呢,在这里其实我们只用引入多项式项即可。
大致意思就是我们把这里的x12、x22 的整体都看成是特征,那么这里x12 前面的系数是1,x22 前面的系数也是1,相应的我们的截距θ0是-r2 ,这里我们得到的决策边界针对x12、x22 来说还是一个线性的决策边界,但是对于x1、x2来说就变成了一个非线性的圆形边界了。也就是说我们可以从线性回归转换到多项式回归的思路。同理可以为我们的逻辑回归算法添加多项式项,基于这样的方式,我们就可以对非线性的数据得到很好的分类,也可以得到曲线的决策边界(这里举了一个特殊的圆,这里还可以改变x12、x22的系数,引入不同的x1、x2,就得到圆心在不同位置的圆或者椭圆)。
二、实现过程
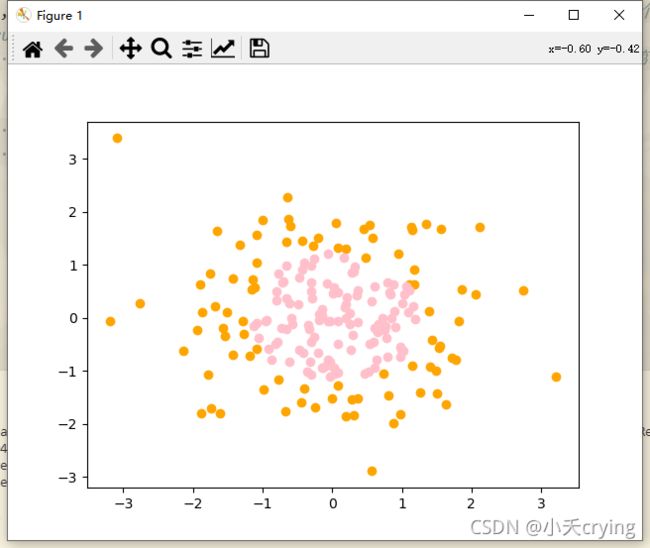
1、绘制样本点
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666) # 添加随机种子
X = np.random.normal(0, 1, size=(200, 2)) # 均值为0,标准差为1的随机序列。200个样本,每个样本2个特征
# 布尔类型转换成int类型,true对应1,false对应0
y = np.array(X[:, 0]**2 + X[:, 1]**2 < 1.5, dtype='int') # X的第一个特征(第一列)的平方+X的第二个特征(第二列)的平方,半径值1.5
# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()
设置200个样本,每个样本2个特征,将x2+y2 <1.5,即圆内的点(粉色点)分类为1,圆外的点(橙色点)分类为0
2、实例化对象
实例化之前,我们还是再次使用之前博客提到的逻辑回归的类,这里再放出来一下
# 逻辑回归类
class logisticsRegression:
def __init__(self):
# 初始化logistics Regression模型
self.coef_ = None # 系数,对应theta1-n,对应的向量
self.interception_ = None # 截距,对应theta0
self._theta = None # 定义私有变量,整体计算的theta
# sigmoid函数数据溢出问题:https://blog.csdn.net/wofanzheng/article/details/103976889
# 定义私有sigmoid函数
# def _sigmoid(self, t):
# return 1. / 1. + np.exp(-t)
def _sigmoid(self, x):
l=len(x)
y=[]
for i in range(l):
if x[i]>=0:
y.append(1.0/(1+np.exp(-x[i])))
else:
y.append(np.exp(x[i])/(np.exp(x[i])+1))
return y
'''
梯度下降
'''
def fit(self, X_train, y_train, eta = 5.0, n_iters = 1e4):
# 根据训练数据集X_train, y_ .train训练logistics Regression模型
# X_train的样本数量和y_train的标记数量应该是一致的
# 使用shape[0]读取矩阵第一维度的长度,在这里就是列数
assert X_train.shape[0] == y_train.shape[0], \
"the size of x_ .train must be equal to the size of y_ train"
# 损失函数
def J(theta, X_b, y):
y_hat = self._sigmoid(X_b.dot(theta))
try:
return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
except:
return float('inf') # 返回float最大值
# 梯度(比较笨的方法)
def dJ(theta, X_b, y):
return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)
# 梯度下降求解theta矩阵
def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
theta = initial_theta
cur_iters = 0
while cur_iters < n_iters:
gradient = dJ(theta, X_b, y) # 求梯度
last_theta = theta # theta重新赋值前,记录上一场的值
theta = theta - eta * gradient # 通过一定的eta学习率取得下一个点的theta
# 最近两点的损失函数差值小于一定精度,退出循环
if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iters += 1
return theta
# 得到X_b
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1]) # 设置n+1维的向量,X_b.shape[1]:第一行的维数
# X_b.T是X_b的转置,.dot是点乘,np.linalg.inv是求逆
# 获取theta
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.interception_ = self._theta[0] # 截距
self.coef_ = self._theta[1:] # 系数
return self
'''
预测可能性的过程
'''
def predict_prob(self, X_predict):
# 给定待预测数据集X_predict,返回表示X_predict的结果概率向量
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return self._sigmoid(X_b.dot(self._theta))
'''
预测过程
'''
def predict(self, X_predict):
# 给定待预测数据集X_predict,返回表示X_predict的结果向量
prob = self.predict_prob(X_predict) # prob向量存储的都是0-1的浮点数
# 进行分类(布尔类型强制转换为整型)
# return np.array(prob >= 0.5, dtype='int')
l = len(prob)
temp_prob=[]
for i in range(l):
if prob[i] >= 0.5:
temp_prob.append(1)
else:
temp_prob.append(0)
return temp_prob
'''
显示属性
'''
def __repr__(self):
return "logisticsRegression()"
这里可以把这整部分内容单独封装成一个文件,每次需要实例化的时候,直接引入
from classLogisticsRegression import logisticsRegression # 引入逻辑回归类对象
然后进行实例化
log_reg = logisticsRegression()
3、添加绘制决策边界方法
'''
绘制决策边界
params-model:训练好的model
params-axis:绘制区域坐标轴范围(0,1,2,3对应x轴和y轴的范围)
'''
def plot_decision_boundary(model, axis):
# meshgrid:生成网格点坐标矩阵
x0, x1 = np.meshgrid(
# 通过linspace把x轴分成无数点
# axis[1] - axis[0]是x的左边界减去x的右边界
# axis[3] - axis[2]:y的最大值减去y的最小值
# arr.shape # (a,b)
# arr.reshape(m,-1) #改变维度为m行、d列 (-1表示列数自动计算,d= a*b /m)
# arr.reshape(-1,m) #改变维度为d行、m列 (-1表示行数自动计算,d= a*b /m )
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
)
print('x0', x0)
# print('x1', x1)
# np.r_是按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等,相加后列数不变。
# np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等,相加后行数不变。
# .ravel():将多维数组转换为一维数组
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
# 这里不能zz = y_predict.reshape(x0.shape),会报错'list' object has no attribute 'reshape'
# 要通过np.array转换一下
zz = np.array(y_predict).reshape(x0.shape)
from matplotlib.colors import ListedColormap
# ListedColormap允许用户使用十六进制颜色码来定义自己所需的颜色库,并作为plt.scatter()中的cmap参数出现:
custom_cmap = ListedColormap(['#F5FFFA', '#FFF59D', '#90CAF9'])
# coutourf([X, Y,] Z,[levels], **kwargs),contourf画的是登高线之间的区域
# Z是和X,Y相同维数的数组。
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
4、绘制决策边界与样本点
# 这里就不划分训练样本和测试样本了,这里直接用所有样本进行训练
log_reg.fit(X, y)
# 绘制决策边界
plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4]) # x、y轴的范围大致都在(-4,4)
# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()
决策边界与样本点
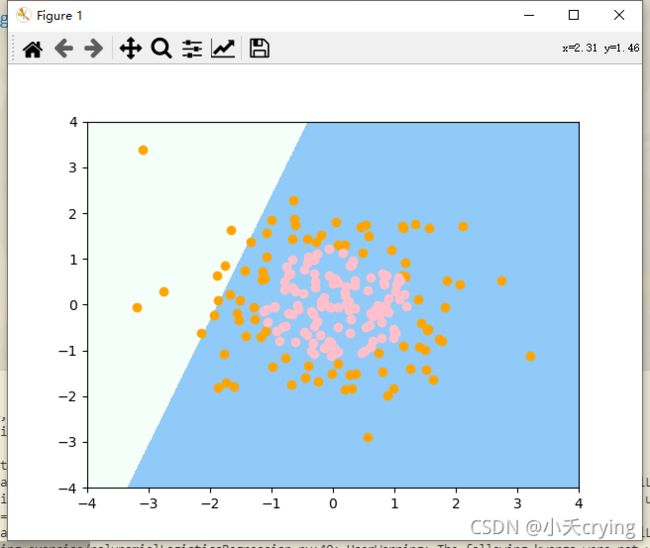
之前的逻辑回归算法本身是使用一条直线对我们的特征平面进行划分,在我们的这个平面对我们的样本点进行划分,显然有很多的错误,接下来我们借助pipeline管道进行实现。
5、pipeline实现多项式回归
在此之前还是把之前逻辑回归的类单独封装,然后进行引入使用
逻辑回归类
# 逻辑回归类
import numpy as np
from sklearn.metrics import accuracy_score
class logisticsRegression:
def __init__(self):
# 初始化logistics Regression模型
self.coef_ = None # 系数,对应theta1-n,对应的向量
self.interception_ = None # 截距,对应theta0
self._theta = None # 定义私有变量,整体计算的theta
# sigmoid函数数据溢出问题:https://blog.csdn.net/wofanzheng/article/details/103976889
# 定义私有sigmoid函数
# def _sigmoid(self, t):
# return 1. / 1. + np.exp(-t)
def _sigmoid(self, x):
l=len(x)
y=[]
for i in range(l):
if x[i]>=0:
y.append(1.0/(1+np.exp(-x[i])))
else:
y.append(np.exp(x[i])/(np.exp(x[i])+1))
return y
'''
梯度下降
'''
def fit(self, X_train, y_train, eta = 5.0, n_iters = 1e4):
# 根据训练数据集X_train, y_ .train训练logistics Regression模型
# X_train的样本数量和y_train的标记数量应该是一致的
# 使用shape[0]读取矩阵第一维度的长度,在这里就是列数
assert X_train.shape[0] == y_train.shape[0], \
"the size of x_ .train must be equal to the size of y_ train"
# 损失函数
def J(theta, X_b, y):
y_hat = self._sigmoid(X_b.dot(theta))
try:
return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
except:
return float('inf') # 返回float最大值
# 梯度(比较笨的方法)
def dJ(theta, X_b, y):
return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)
# 梯度下降求解theta矩阵
def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
theta = initial_theta
cur_iters = 0
while cur_iters < n_iters:
gradient = dJ(theta, X_b, y) # 求梯度
last_theta = theta # theta重新赋值前,记录上一场的值
theta = theta - eta * gradient # 通过一定的eta学习率取得下一个点的theta
# 最近两点的损失函数差值小于一定精度,退出循环
if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iters += 1
return theta
# 得到X_b
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1]) # 设置n+1维的向量,X_b.shape[1]:第一行的维数
# X_b.T是X_b的转置,.dot是点乘,np.linalg.inv是求逆
# 获取theta
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.interception_ = self._theta[0] # 截距
self.coef_ = self._theta[1:] # 系数
return self
'''
预测可能性的过程
'''
def predict_prob(self, X_predict):
# 给定待预测数据集X_predict,返回表示X_predict的结果概率向量
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return self._sigmoid(X_b.dot(self._theta))
'''
预测过程
'''
def predict(self, X_predict):
# 给定待预测数据集X_predict,返回表示X_predict的结果向量
prob = self.predict_prob(X_predict) # prob向量存储的都是0-1的浮点数
# 进行分类(布尔类型强制转换为整型)
# return np.array(prob >= 0.5, dtype='int')
l = len(prob)
temp_prob=[]
for i in range(l):
if prob[i] >= 0.5:
temp_prob.append(1)
else:
temp_prob.append(0)
return temp_prob
'''
预测准确度
'''
def score(self, X_test, y_test):
# 根据测试数据集 X_test 和y_test 确定当前模型的准确度
y_predict = self.predict(X_test)
return accuracy_score(y_test, y_predict)
'''
显示属性
'''
def __repr__(self):
return "logisticsRegression()"
管道包装多项式回归
from classLogisticsRegression import logisticsRegression # 引入逻辑回归类对象
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
# 包装管道进行多项式回归(传入degree,返回多项式回归的类)
def PolynomialLogisticsRegression(degree):
# 使用pipeline创建管道,送给poly_reg对象的数据会沿着管道的三步依次进行
return Pipeline([ # Pipeline传入的是列表,列表中传入管道中每一步对应的类(这个类以元组的形式进行传送)
("poly", PolynomialFeatures(degree=degree)), # 第一步:求多项式特征,相当于poly = PolynomialFeatures(degree=2)
("std_scaler", StandardScaler()), # 第二步:数值的均一化
("log_reg", logisticsRegression()) # 第三步:进行逻辑回归操作
])
poly_log_reg = PolynomialLogisticsRegression(2)
poly_log_reg.fit(X, y)
# 查询分类准确度
print('分类准确度', poly_log_reg.score(X, y))
![]()
可以看到这个分类准确度是非常高了。
接下来绘制决策边界
# 绘制决策边界
plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4]) # x、y轴的范围大致都在(-4,4)
# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()
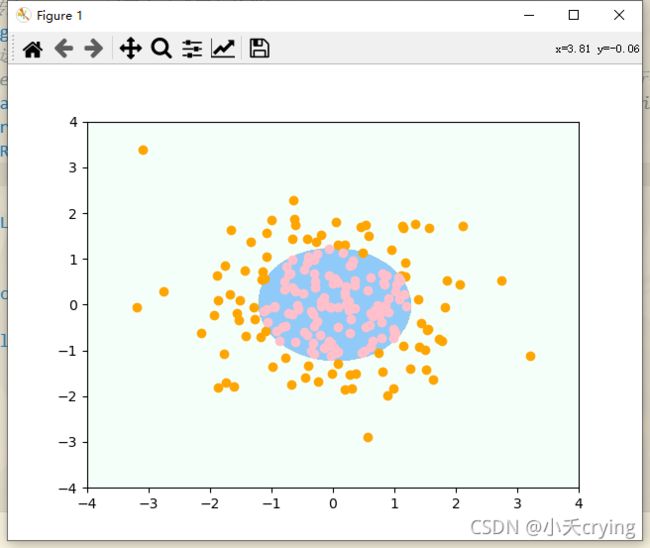
绘制决策边界后,我们可以看到决策边界相当于一个圆形,可以很好的对非线性数据进行划分。但是实际上遇到的数据不可能这么圆,如果是很奇怪的参数,我们的degree就要相应选取其他的值。接下来试一下degree选取其他的值。
degree=20
''' degree=20 '''
poly_log_reg2 = PolynomialLogisticsRegression(20)
poly_log_reg2.fit(X, y)
# 查询分类准确度
print('degree=20分类准确度', poly_log_reg2.score(X, y))
# 绘制决策边界
plot_decision_boundary(poly_log_reg2, axis=[-4, 4, -4, 4]) # x、y轴的范围大致都在(-4,4)
# 绘制样本
plt.scatter(X[y == 0, 0], X[y == 0, 1], color = "orange")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color = "pink")
plt.show()

在这个图像外面,决策边界很奇怪,这个外围的边界其实并不是我们想要的,出现这种情况是因为我们的degree=20这个degree太大了,导致形状不规则,这种情况下属于过拟合了。
解决过拟合的思路:最简单的就是降低degree的值,另外就是对模型进行正则化。