面向JavaScript入门初学者的二叉搜索树算法教程

目录

• 什么是二叉搜索树 (BST)？
  
• 二叉树基本遍历（中序、后序、前序）
  
• 中序遍历
  
• 后序遍历
  
• 前序遍历
  
• 什么是有效的二叉搜索树？
  
• 如何找到二叉树最大深度
  
• 如何找到两个树节点之间的最小公共祖先
  
• 结尾想说的
  

在本文中，我将尽力解释一些您在编码面试之前应该学习的核心算法。

什么是二叉搜索树 (BST)？

在编码面试中很常见，BST 是一种树状数据结构，顶部有一个根。它们是存储数值的好方法，因为它们的有序性质允许快速搜索和查找。

与普通树相比，BST 具有以下特性：

• 每个左孩子的值都比它的父母小
• 每个右孩子的值都比它的父母大
• 每个节点可以包含 0 到 2 个子节点。

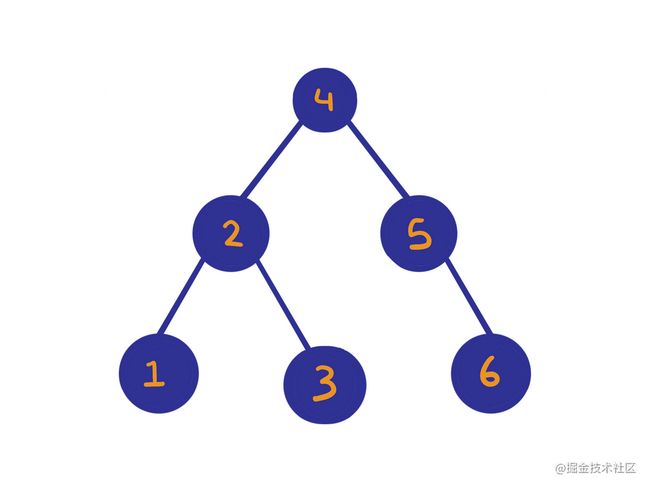
下图应该更清楚地说明事情。

二叉树节点的定义

我们通常在 Javascript 中定义一个二叉树节点，函数如下：

 function TreeNode(val, left, right) {
     this.val = val
     this.left = left
     this.right = right
 }

二叉树基本遍历（中序、后序、前序）

首先要知道如何遍历 BST 的每个节点。这允许我们在 BST 的所有节点上执行一个功能。例如，如果我们想x在 BST 中找到一个值，我们就需要节点。

有三种主要方法可以做到这一点。幸运的是，他们有共同的主题。

中序遍历

递归算法是开始使用二叉树中序遍历的最简单方法。思路如下：

• 如果节点为空，则什么都不做——否则，递归调用节点左子节点上的函数。
• 然后，遍历完所有左子节点后，对节点进行一些操作。我们当前的节点保证是最左边的节点。
• 最后，调用 node.right 上的函数。

Inorder 算法从左、中、右遍历树节点。

const inorder = (root) => {
    const nodes = []
    if (root) {
        inorder(root.left)
        nodes.push(root.val)
        inorder(root.right)
    }
    return nodes
}
// 对于我们的示例树，将返回 [1,2,3,4,5,6]

后序遍历

递归算法是开始后序遍历的最简单方法。

• 如果节点为空，则什么都不做——否则，递归调用节点左子节点上的函数。
• 当没有更多的左孩子时，调用 node.right 上的函数。
• 最后，在节点上做一些操作。

后序遍历从左、右、中访问树节点。

const postorder = (root) => {
    const nodes = []
    if (root) {
        postorder(root.left)
        postorder(root.right)
        nodes.push(root.val)
    }
    return nodes
}
// 对于我们的示例树，将返回 [1,3,2,6,5,4]

前序遍历

递归算法是开始前序遍历的最简单方法。

• 如果节点为空，则什么都不做——否则，在节点上做一些操作。
• 遍历节点的左子节点并重复。
• 遍历到节点的右孩子并重复。

后序遍历从中、左、右访问树节点。

const preorder = (root) => {
    const nodes = []
    if (root) {
        nodes.push(root.val)
        preorder(root.left)
        preorder(root.right)
    }
    return nodes
}
// 对于我们的示例树，将返回 [4,2,1,3,5,6]

什么是有效的二叉搜索树？

有效的二叉搜索树 (BST) 具有所有值小于父节点的左子节点，以及值大于父节点的所有右子节点。
要验证一棵树是否是有效的二叉搜索树：

• 定义当前节点可以具有的最小值和最大值
• 如果节点的值不在这些范围内，则返回 false
• 递归验证节点的左孩子，最大边界设置为节点的值
• 递归验证节点的右孩子，最小边界设置为节点的值

const isValidBST = (root) => {
    const helper = (node, min, max) => {
        if (!node) return true
        if (node.val <= min || node.val >= max) return false
        return helper(node.left, min, node.val) && helper(node.right, node.val, max)
    }
    return helper(root, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER)
}

如何找到二叉树最大深度

在这里，算法试图找到我们 BST 的高度/深度。换句话说，我们正在查看 BST 包含多少个“级别”。

• 如果节点为空，我们返回 0 因为它没有添加任何深度
• 否则，我们将 + 1 添加到我们当前的深度（我们遍历了一层）
• 递归计算节点子节点的深度并返回node.left和node.right之间的最大和

const maxDepth = function(root) {
    const calc = (node) => {
        if (!node) return 0
        return Math.max(1 + calc(node.left), 1 + calc(node.right))
    }
    return calc(root)
};

如何找到两个树节点之间的最小公共祖先

让我们提高难度。我们如何在我们的二叉树中找到两个树节点之间的共同祖先？让我们看一些例子。

在这棵树中，3和1的最低共同祖先是2。3和2的LCA是2。6和1和6的LCA是4。

看到这里的模式了吗？两个树节点之间的 LCA 要么是节点本身之一（3 和 2 的情况），要么是父节点，其中第一个子节点位于其左子树中的某处，而第二个子节点位于其右子树中的某处。

寻找两个树节点 p 和 q 之间的最低共同祖先（LCA）的算法如下：

• 验证是否在左子树或右子树中找到 p 或 q
• 然后，验证当前节点是 p 还是 q
• 如果在左子树或右子树中找到 p 或 q 之一，并且 p 或 q 之一是节点本身，我们就找到了 LCA
• 如果在左子树或右子树中都找到了 p 和 q，我们就找到了 LCA

const lowestCommonAncestor = function(root, p, q) {
    let lca = null
    const isCommonPath = (node) => {
        if (!node) return false
        var isLeft = isCommonPath(node.left)
        var isRight = isCommonPath(node.right)
        var isMid = node == p || node == q
        if (isMid && isLeft || isMid && isRight || isLeft && isRight) {
            lca = node
        }
        return isLeft || isRight || isMid
    }
    isCommonPath(root)
    return lca
};

结尾想说的

到此，我们已经学会了如何遍历、验证和计算 BST 的深度。

到此这篇关于面向JavaScript入门初学者的二叉搜索树算法教程的文章就介绍到这了,更多相关JavaScript二叉搜索树算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！