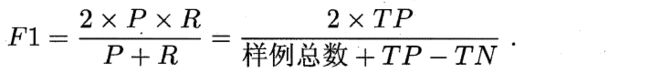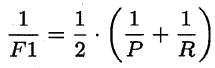吃瓜笔记01-02 机器学习绪论与模型评估指标
学习内容:西瓜书和南瓜书--第1~2章
讲解课程:Datawhale吃瓜教程(【吃瓜教程】《机器学习公式详解》(南瓜书)与西瓜书公式推导直播合集_哔哩哔哩_bilibili)
目录
第1章 绪论
1.1-1.2 基本概念
1.3 假设空间
1.4 归纳偏好
第2章 模型评估与选择
2.1 误差、过拟合
2.2 模型评估方法
2.3 性能度量
2.5 方差与偏差
第1章 绪论
1.1-1.2 基本概念
1. 机器学习:假设用P来评估计算机程序在某任务类T上的性能,若一个程序通过利用经验E在T中任务上获得了性能改善,则我们就说关于T和P,该程序对E进行了学习.
本书用“模型”泛指从数据中学得的结果,有文献用“模型”指全局性结果(例如一棵决策树),而用“模式”指局部性结果(例如一条规则).
2. 数据划分:
数据集<==样本(示例,特征向量)<==特征(特征值)
数据集分为:训练集,测试集
训练样本由多个特征和标记组成。
从数据中学得模型的过程称为“学习”(learning)或“训练”(training)。
学得模型对应了关于数据的某种潜在的规律,因此亦称“假设”(hypothesis);这种潜在规律自身,则称为“真相”或“真实”(ground-truth),学习过程就是为了找出或逼近真相。本书有时将模型称为“学习器”(learner),可看作学习算法在给定数据和参数空间上的实例化.
3. 常见的任务类型:
- 分类与回归的区别:分类预测离散值,回归预测连续值
- 聚类:将测试样本聚合为多个“簇”,训练过程不需要标签
泛化能力:学得模型对训练集之外样本的预测能力,泛化能力越强模型越好。
4. 科学推理分为:
- 归纳推理:由小及大,特殊到一般(泛化)
- 演绎推理:由大推小,从基础定理或事实中推导出结果(特化)
由此可知,机器学习是一种“归纳学习”方法。狭义的归纳学习指从训练样本中学到概念。现在的技术还难以形成明确且性能好的概念。
1.3 假设空间
假设空间=是选择特征的空间还是某种函数的限制?
机器学习中可能的函数构成的空间称为“假设空间”,也就是由输入空间 X 到输出空间 Y 的映射 f : X->Y 所构成的集合。
样本空间是所有可能的输入样本的特征向量组成,如西瓜还有西瓜形状,花纹等特征,样本空间有无穷多个。假设空间由选取的特征的所有可能取值组成。版本空间是假设空间中筛选的符合目前数据集的假设集合。样本空间>假设空间>版本空间
学习过程:可以理解为对所有假设空间(hypothesis space)进行搜索,找到最匹配的假设。
1.4 归纳偏好
归纳偏好:一种假设,什么样的模型更好,有某种判断标准。
奥卡姆剃刀原则:主张选择与经验观察一致的最简单假设。
“没有免费的午餐”定理(No Free Lunch Theorem,简称NFL定理):无论学习算法多聪明或者多笨拙,它们的期望性能竟然相同。算法总在一些问题下表现好,一些问题下表现坏。
要谈论算法的相对优劣,必须要针对具体的学习问题。学习算法自身的归纳偏好与问题是否相配,往往会起到决定性的作用。
机器学习的兴起:
- 连接主义-如感知机,神经网络
- 符号主义-基于逻辑学习,如决策树
- 统计学习-SVM,核方法
第2章 模型评估与选择
2.1 误差、过拟合
训练(经验)误差,泛化(测试)误差
过拟合--欠拟合:
2.2 模型评估方法
2.2.1 常见方法
1. 留出法(hold-out):直接将数据集划分为两个互斥的集合。
对于分类问题,按照类别比例采样。保证训练集与测试集是独立同分布。
2. 交叉验证法(cross validation):将数据集划分为k个大小相似的互斥子集。
每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集;这样就可进行k次训练和测试,最终返回的是这k个测试结果的均值。其结果的稳定性很大程度上取决于k的值。
3. 自助采样法(bootstrap sampling):是随机采样得到的采样集D'训练,用原始数据集D测试(约36.8%的不同)。适用于较小的数据集。
对于m个样本的原始训练集,我们每次先随机采集一个样本放入采样集,接着把该样本放回,也就是说下次采样时该样本仍有可能被采集到,这样采集m次,最终可以得到m个样本的采样集,由于是随机采样,这样每次的采样集是和原始训练集不同的,和其他采样集也是不同的。
2.2.2 调参与模型选择
在进行模型评估与选择时,除了要对适用学习算法进行选择,还需对算法参数进行设定,这就是通常所说的“调参”。
模型评估与选择中用于评估测试的数据集常称为“验证集"(validation set). 在研究对比不同算法的泛化性能时,我们用测试集上的判别效果来估计模型在实际使用时的泛化能力,而把训练数据另外划分为训练集和验证集,通过在验证集上的性能来进行模型选择和调参.
2.3 性能度量
| 预测结果 | 合计 | ||
| 真实情况 | 正例 | 反例 | |
| 正例 | TP(真正例) | FN(假反例) | TP+FN(所有正例) |
| 反例 | FP(假正例) | TN(真反例) | FP+TN(所有负例) |
| 合计 | TP+FP(预测为正) | FN+TN(预测为反) | N(所有样本) |
一、错误率与精度
1、准确率(精度):被分对的样本比例
ACC = ( TP + TN )/ All
2、错误率:被分错的样本比例
ERR = ( FP + FN )/ All
二、查准率、查全率与F1
3、查准率(真正例率):被分为正例中,有多少是正例
Pre = TP / (TP + FP)
4、召回率(查全率/灵敏度):样本中的正例多少个被预测正确了
Recall = TP / (TP + FN )
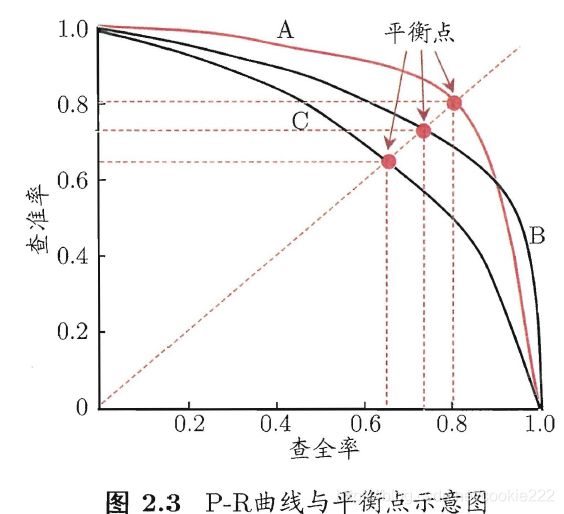
查准率和查全率是一对矛盾的度量,一般来说,查准率高时,查全率往往偏低;而查全率高时,查准率往往偏低.
P-R图直观地显示出学习器在样本总体上的查全率、查准率,“平衡点”(简称BEP)就是综合两者的一个度量,它是“查准率=查全率”时的取值。
更常用的是F1度量:基于查准率与查全率的调和平均。
三、ROC与AUC曲线
ROC全称是“受试者工作特征”(Receiver Operating Characteristic)曲线。ROC曲线的纵轴是“真正例率"(True Positive Rate),横轴是“假正例率"(False Positive Rate),两者分别定义为:
TPR = TP /(TP+FN)
FPR = FP /(TN+FP)
ROC曲线有一个很好的特征:在实际的数据集中经常会出现类别不平衡现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间而变化。而在这种情况下,ROC曲线能够保持不变。
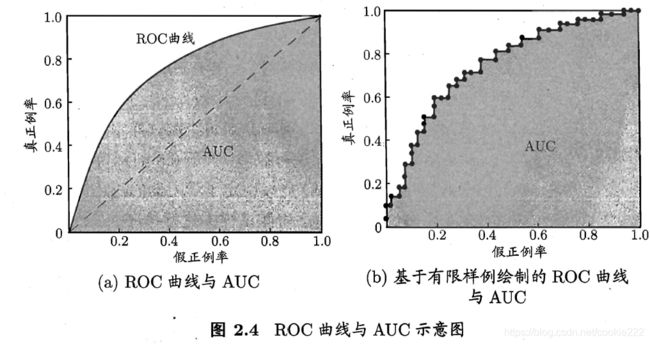
判断标准:进行学习器的比较时,与P-R图相似,若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以一般性地断言两者孰优孰劣,此时如果一定要进行比较,则较为合理的判据是比较ROC曲线下的面积,即AUC(Area Under ROC Curve),如图2.4所示.
首先AUC是一个概率值(0.5~1之间),当随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的分数将这个正样本排在负样本前面的概率就是AUC值。所以,AUC的值越大,当前的分类算法越有可能将正样本排在负样本值前面,既能够更好的分类。
四、代价曲线:略
五、假设检验(属于统计知识):略
2.5 方差与偏差
偏差-方差分解试图对学习算法的泛化错误率期望进行拆解。泛化误差E可分解为偏差平方、方差与噪声之和。
回顾偏差、方差、噪声的含义:
偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力;方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响;噪声则表达了在当前任务上任何算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度。
偏差-方差分解说明,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的.给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小.
偏差-方差是一对矛盾的度量。方差和偏差一般是反向变化的,复杂模型方差大,偏差小;简单模型方差小,偏差大。当方差减小的量大于偏差增加的量时,模型的测试误差减小。