从零开始手写VIO第五章作业（含理论说明及编程思维过程）

前言·与同主题博文的不同

延续该系列博文的风格，本博文站在前人优秀博文的基础上，尽量补充同主题博文所没有涉及到的关键点。之前同主题优秀博文已经讲解非常清楚的部分，本博文中将直接给出链接，对于之前博文没有涉及到的点，本博文会重点阐述。除此之外，还包含小编在学习过程中遇到的问题，欢迎有兴趣的朋友讨论交流。
对于第五章，所补充的关键点包含以下几个方面：代码和课件中的公式符号不统一的地方，第一题和第二题舒尔补公式形式的区别，论文总结题原论文中不易理解公式的说明，提升题第二题的原始代码中prior对应的残差和雅克比矩阵计算的说明及作业代码的说明。

1.完成单目 Bundle Adjustment (BA) 求解器 problem.cc 中的部分代码

完成本章所有作业的前提是至少看懂整个代码框架及部分代码细节，这里小编推荐一篇对代码分析相当详细的博文：[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析。

1.1完成 Problem::MakeHessian() 中信息矩阵 H 的计算

先直接给出代码：

// TODO:: home work. 完成 H index 的填写.
H.block(index_i, index_j, dim_i, dim_j).noalias() += hessian;
if (j != i) {
     
	// 对称的下三角
	// TODO:: home work. 完成 H index 的填写.
    H.block(index_j, index_i, dim_j, dim_i).noalias() += hessian.transpose();
}

代码中关于函数noalias()的相关说明请参考博文：Eigen中的noalias()： 解决矩阵运算的混淆问题。
代码中涉及到的理论可以参考高翔《视觉SLAM十四讲》P250的图（10.3）和公式（10.52）前后的内容，如下图：

针对本问题如何具体应用上述理论具体可以参考博文从零手写VIO(五)或者其它同主题博文中的相关内容。

1.2完成 Problem::SolveLinearSystem() 中 SLAM 问题的求解

1.2.1理论及代码

这里的理论参考如下：

有几点需要强调。第一、上面图中的角标l在代码中替换为了m；第二、代码中所有与b相关的变量其实已经包含了负号，而上图中的公式没有包含，所以再应用上图公式的时候，只需要将与b相关的公式的符号都取反即可（包括bp和bl）。
第一部分代码如下，其中要说明的是，正如下面代码最开始部分所定义，reserve_size = ordering_poses_，marg_size = ordering_landmarks_，代码中这两组变量选择哪一组都可以。小编选择了ordering_poses_和 ordering_landmarks_。

// SLAM 问题采用舒尔补的计算方式
// step1: schur marginalization --> Hpp, bpp
int reserve_size = ordering_poses_;
int marg_size = ordering_landmarks_;
// TODO:: home work. 完成矩阵块取值，Hmm，Hpm，Hmp，bpp，bmm
MatXX Hmm = Hessian_.block(ordering_poses_, ordering_poses_, ordering_landmarks_, ordering_landmarks_);
MatXX Hpm = Hessian_.block(0, ordering_poses_, ordering_poses_, ordering_landmarks_);
MatXX Hmp = Hessian_.block(ordering_poses_, 0, ordering_landmarks_, ordering_poses_);
VecX bpp = b_.segment(0, ordering_poses_);
VecX bmm = b_.segment(ordering_poses_, ordering_landmarks_);

第二部分代码如下：

// TODO:: home work. 完成舒尔补 Hpp, bpp 代码
MatXX tempH = Hpm * Hmm_inv;
H_pp_schur_ = Hessian_.block(0, 0, ordering_poses_, ordering_poses_) - tempH * Hmp;
b_pp_schur_ = bpp - tempH * bmm;

第三部分代码如下：

// TODO:: home work. step3: solve landmark
VecX delta_x_ll(marg_size);
delta_x_ll = Hmm_inv * (bmm - Hmp * delta_x_pp);
delta_x_.tail(marg_size) = delta_x_ll;

1.2.2仿真结果及分析

在文件TestMonoBA.cpp的第80行和第81行有如下代码（代码的效果是使两帧位姿对应的雅克比为 0，之后会给出对应的代码），如果注释掉，则表示不固定第一帧和第二帧。

//        if(i < 2)
//            vertexCam->SetFixed();

对应的设置雅克比矩阵为零的代码截图如下：

编译说明：

cd BA_schur  \\ 进入文件夹
mkdir build   
cd build
cmake ..
make -j4    
cd app
./testMonoBA

不固定第一帧和第二帧，仿真结果如下：

使用文件TestMonoBA.cpp的第80行和第81行的代码固定第一帧和第二帧后，仿真结果如下：

仿真结果分析：通过对比固定第一帧和第二帧前后的优化结果，可以看出，利用 LM 算法，在优化完成后，两种方式得到的空间点的逆深度与真值都很相近，但是，固定前，第一帧相机 pose 的位置不再是(0, 0, 0)；而在固定后，使两帧位姿对应的雅克比为 0，信息矩阵中对应位置的矩阵块也为 0，利用 LM 算法求解时，相当于固定了第一帧和第二帧位姿不被优化，也就不会发生改变。

2.完成滑动窗口算法测试函数

2.1完成 Problem::TestMarginalize() 中的代码，并通过测试

原代码中给出了将 col i 移动矩阵最右边的代码，仿照这部分换列代码不难写出homework中的换行代码。
第一部分代码如下：

// TODO:: home work. 将变量移动到右下角
/// 准备工作： move the marg pose to the Hmm bottown right
// 将 row i 移动矩阵最下面
Eigen::MatrixXd temp_rows = H_marg.block(idx, 0, dim, reserve_size);
Eigen::MatrixXd temp_botRows = H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size);
H_marg.block(idx, 0, reserve_size - idx - dim, reserve_size) = temp_botRows;
H_marg.block(reserve_size - dim, 0, dim, reserve_size) = temp_rows;

第二部分要求完成舒尔补操作，这里注意这里被marg的变量现在到了矩阵的右下角（不像前面作业中的再左上角），所用的舒尔补公式略有不同，公式如下图：

第二部分代码如下：

// TODO:: home work. 完成舒尔补操作
Eigen::MatrixXd Arm = H_marg.block(0, n2, n2, m2);
Eigen::MatrixXd Amr = H_marg.block(n2, 0, m2, n2);
Eigen::MatrixXd Arr = H_marg.block(0, 0, n2, n2);

仿真结果如下：

从上图可以看出，在 marg 变量 V2 之前，变量 V1 与变量 V3 信息矩阵对应位置为 0，即 V1 与 V3关于 V2 条件独立，将 V2 移到右下角并 marg 之后，变量 V1 与变量 V3 产生联系，信息矩阵对应位置不再是 0，即 V2 被 marg 后将信息传递给了 V1 与 V3。

3.总结论文

对论文的总结参考博文：[论文笔记|VIO]On the Comparison of Gauge Freedom Handling in Optimization-based V-I State Estimation。
小编在这里要对论文中几处不太好理解的公式做出说明。第一、为什么红框1处的表达式不能相对于初始旋转 R0 固定 yaw 角；第二、红框2处为什么能相对于初始旋转 R0 固定 yaw 角，与1处相比，2处做了什么事情。

首先是第一个问题，每次旋转之后的x轴和y轴只与这次旋转之后得到的z轴正交，并不与旋转之前的z轴或者最初的z轴正交，所以，即使每次旋转的时候都强制z轴分量为0，只要x轴和y轴不与最初的z轴正交，那么旋转矢量在最初的z轴方向还是会存在不为0的分量。这样就相当于绕最初的z轴旋转了，那么yaw角就没有被固定。
第二个问题，一次相乘就表示一次旋转，∆φ相当于把前面的连乘先算出来（把后面的旋转合并成一个旋转），最后再与R00相乘（最后相对于最初的坐标系旋转一次），每次更新前面连乘的结果∆φ，这样保证了R00与最后的R0只有一次相乘运算，也就是只有一次旋转，结合第一个问题与上图强制这一次旋转z轴分量为0的公式（10），这样就保证了yaw角是固定的。

4.在代码中给第一帧和第二帧添加 prior 约束，并比较为 prior 设定不同权重时, BA 求解收敛精度和速度

首先要说明的是，这个部分小编是站在之前的优秀博文从零开始手写VIO第三期作业总结(仅供参考)的肩膀上完成的，原博文直接给出了结果，小编在其中增加了自己思考的过程，并将其以阅读性较强的方式记录如下。
添加 prior 约束相当于多了新的测量，只需要增加对应的edge以及处理edge中相关残差和雅克比等变量的代码，老师所提供的代码已经将除添加新的测量（prior约束的对应的edge）以外的部分都写好了，这里只需要添加对应的edge即可。

4.1残差和雅克比矩阵的计算

除添加新的edge相关的代码外，小编觉得最重要的是残差和雅克比的计算，这两部分老师写在了文件edge_prior.cpp中，小编在这里给出。值得说明的是，代码中给出了一个参考文献IMU Preintegration on Manifold for Efficient Visual-Inertial Maximum-a-Posteriori Estimation，文献篇幅较长，有兴趣的朋友可以精读一下。
计算残差对应的代码如下：

// TODO:: home work. 完成舒尔补操作
void EdgeSE3Prior::ComputeResidual() {
     
    VecX param_i = verticies_[0]->Parameters();
    Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]);
    Vec3 Pi = param_i.head<3>();

//    std::cout << Qi.vec().transpose() <<" "<< Qp_.vec().transpose()<
    // rotation error
#ifdef USE_SO3_JACOBIAN
    Sophus::SO3d ri(Qi);
    Sophus::SO3d rp(Qp_);
    Sophus::SO3d res_r = rp.inverse() * ri;
    residual_.block<3,1>(0,0) = Sophus::SO3d::log(res_r);
#else
    residual_.block<3,1>(0,0) = 2 * (Qp_.inverse() * Qi).vec();
#endif
    // translation error
    residual_.block<3,1>(3,0) = Pi - Pp_;
//    std::cout << residual_.transpose() <
}

计算雅克比矩阵对应的代码如下：

void EdgeSE3Prior::ComputeJacobians() {
     

    VecX param_i = verticies_[0]->Parameters();
    Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]);

    // w.r.t. pose i
    Eigen::Matrix<double, 6, 6> jacobian_pose_i = Eigen::Matrix<double, 6, 6>::Zero();

#ifdef USE_SO3_JACOBIAN
    Sophus::SO3d ri(Qi);
    Sophus::SO3d rp(Qp_);
    Sophus::SO3d res_r = rp.inverse() * ri;
    // http://rpg.ifi.uzh.ch/docs/RSS15_Forster.pdf  公式A.32
    jacobian_pose_i.block<3,3>(0,3) = Sophus::SO3d::JacobianRInv(res_r.log());
#else
    jacobian_pose_i.block<3,3>(0,3) = Qleft(Qp_.inverse() * Qi).bottomRightCorner<3, 3>();
#endif
    jacobian_pose_i.block<3,3>(3,0) = Mat33::Identity();

    jacobians_[0] = jacobian_pose_i;
//    std::cout << jacobian_pose_i << std::endl;
}

4.2编程思路和代码分析

我们仿照老师所给文件TestMonoBA.cpp代码中构建重投影误差edge的代码来构建第一帧和第二帧添加 prior 约束edge的代码。
原始代码中构建重投影误差edge的代码如下：

for (size_t j = 1; j < cameras.size(); ++j) {
     
    Eigen::Vector3d pt_i = cameras[0].featurePerId.find(i)->second;
    Eigen::Vector3d pt_j = cameras[j].featurePerId.find(i)->second;
    shared_ptr<EdgeReprojection> edge(new EdgeReprojection(pt_i, pt_j));
    edge->SetTranslationImuFromCamera(qic, tic);

    std::vector<std::shared_ptr<Vertex> > edge_vertex;
    edge_vertex.push_back(verterxPoint);
    edge_vertex.push_back(vertexCams_vec[0]);
    edge_vertex.push_back(vertexCams_vec[j]);
    edge->SetVertex(edge_vertex);

    problem.AddEdge(edge);
}

仿照上述代码构建第一帧和第二帧添加 prior 约束edge的代码的过程中还有一个点需要注意，我们需要设定不同权重，也就是需要设定不同的信息矩阵。原始代码中，类Edge在初始化的构造函数中就设定了默认为单位矩阵的信息矩阵的代码截图如下：

所以设定不同的权重，只需要对原来的信息矩阵乘以相对应的标量即可，代码如下：

double Wp = 0;
for (size_t k = 0; k < 2; ++k) {
     
    shared_ptr<EdgeSE3Prior> edge_prior(new EdgeSE3Prior(cameras[k].twc, cameras[k].qwc));
    std::vector<std::shared_ptr<Vertex> > edge_prior_vertex;
    edge_prior_vertex.push_back(vertexCams_vec[k]);
    edge_prior->SetVertex(edge_prior_vertex);
    edge_prior->SetInformation(edge_prior->Information() * Wp);
    problem.AddEdge(edge_prior);
}

除此以外，还需要在文件TestMonoBA.cpp中添加对应的头文件backend/edge_prior.h，代码如下：

#include <iostream>
#include <random>
#include "backend/vertex_inverse_depth.h"
#include "backend/vertex_pose.h"
#include "backend/edge_reprojection.h"
#include "backend/problem.h"
#include "backend/edge_prior.h"

4.3仿真结果及分析

在为第一帧和第二帧添加先验约束后，设置了不同先验权重,，比较收敛精度和收敛速度。
以权重为 0和10⁸为例，给出仿真结果图：
其中当先验权重 Wp = 0 时，仿真结果入下：

其中当先验权重Wp = 10⁸ 的运行结果如下图所示：

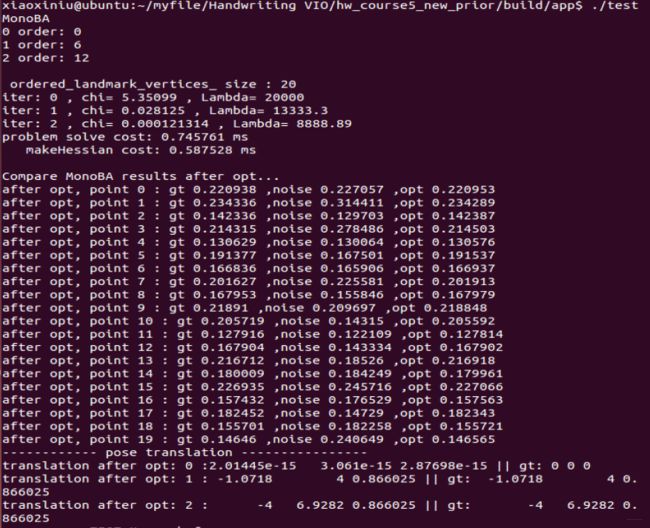
收敛后的精度非常接近，这里不再深入说明。下面是收敛速度的统计表：

与3中的论文所得到的的结论一致，当先验权值大于一定值时，迭代次数和收敛时间趋于稳定，当先前的权重从0增加到稳定的阈值时，在计算时间上会有一个峰值。