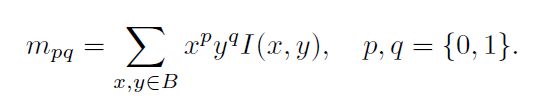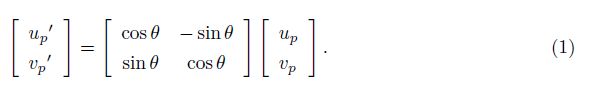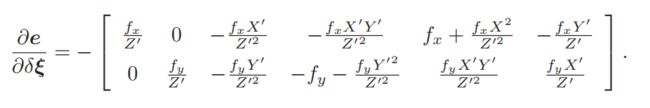视觉SLAM入门 -- 学习笔记 - Part5
2 ORB 特征点
原图见1.png 文件和2.png。
2.1 ORB 提取
ORB 即Oriented FAST 简称。它实际上是FAST 特征再加上一个旋转量。本习题将使用OpenCV 自带的FAST 提取算法，但是你要完成旋转部分的计算。旋转的计算过程描述如下：
在一个小图像块中，先计算质心。质心是指以图像块灰度值作为权重的中心。
-
在一个小的图像块B 中，定义图像块的矩为：
-
通过矩可以找到图像块的质心：
-
连接图像块的几何中心O 与质心C，得到一个方向向量 O C ⃗ \vec{OC} OC，于是特征点的方向可以定义为：
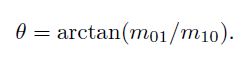
实际上只需计算 m 01 m_{01} m01 和 m 10 m_{10} m10 即可。习题中取图像块大小为16x16，即对于任意点(u, v)，图像块从(u - 8, v - 8) 取到(u + 7, v + 7) 即可。请在习题的computeAngle 中，为所有特征点计算这个旋转角。
提示：
- 由于要取图像16x16 块，所以位于边缘处的点（比如u < 8 的）对应的图像块可能会出界，此时 需要判断该点是否在边缘处，并跳过这些点。
- 由于矩的定义方式，在画图特征点之后，角度看起来总是指向图像中更亮的地方。
- std::atan 和std::atan2 会返回弧度制的旋转角，但OpenCV 中使用角度制，如使用std::atan 类函数，请转换一下。
作为验证，第一个图像的特征点如图1 所示。看不清可以放大看。
图1: 带有旋转的FAST
computeAngle()
/**
* compute the angle for ORB descriptor
* @param [in] image input image
* @param [in|out] detected keypoints
*/
#define Rad_to_deg 45.0 / atan(1.0)
void computeAngle(const cv::Mat &img, vector<cv::KeyPoint> &keypoints) {
int half_patch_size = 8;
for (auto &kp : keypoints) {
// START YOUR CODE HERE (~7 lines)
if (kp.pt.x < half_patch_size || kp.pt.y < half_patch_size ||
kp.pt.x >= img.cols - half_patch_size || kp.pt.y >= img.rows - half_patch_size) {
//outside
// bad_points++;
// descriptors.push_back({});
continue;
}
float m01 = 0, m10 = 0;
for (int dx = -half_patch_size; dx < half_patch_size; ++dx) {
for (int dy = -half_patch_size; dy < half_patch_size; ++dy) {
uchar pixel = img.at<uchar>(kp.pt.y + dy, kp.pt.x + dx);
m10 += dx * pixel;
m01 += dy * pixel;
}
}
// angle should be arc tan(m01/m10);
kp.angle = atan(m01 / m10) * Rad_to_deg; // compute kp.angle
// float m_sqrt = sqrt(m01 * m01 + m10 * m10) + 1e-08; // avoid divide by zero
// float sin_theta = m01/m_sqrt;
// float cos_theta = m10/m_sqrt;
// END YOUR CODE HERE
}
// return;
}
2.2 ORB 描述
ORB 描述即带旋转的BRIEF 描述。所谓BRIEF 描述是指一个0-1 组成的字符串（可以取256 位或128 位），每一个bit 表示一次像素间的比较。算法流程如下：
- 给定图像I 和关键点(u，v)，以及该点的转角 θ \theta θ。以256 位描述为例，那么最终描述子
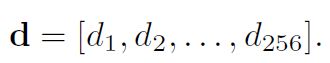
2. 对任意i = 1, … , 256， d i d_{i} di 的计算如下。取(u, v) 附近任意两个点p, q，并按照 θ \theta θ 进行旋转：
推导可参考：
https://www.cnblogs.com/meteoric_cry/p/7987548.html
其中 u p u_{p} up, v p v_{p} vp 为p 的坐标，对q 亦然。记旋转后的p, q 为p′, q′，那么比较I(p′) 和I(q′)，若前者大，记 d i d_{i} di = 0，反之记 d i d_{i} di = 1。(注意反过来记也可以，但是程序中要保持一致。)
这样我们就得到了ORB 的描述。我们在程序中用256 个bool 变量表达这个描述。(严格来说可以用32 个uchar 以节省空间，但是那样涉及到位运算，本习题只要求掌握算法)
请你完成compute-ORBDesc 函数，实现此处计算。注意，通常我们会固定p, q 的取法（称为ORB 的pattern），否则每次都重新随机选取，会使得描述不稳定。我们在全局变量ORB_pattern 中定义了p, q 的取法，格式为 u p u_{p} up, v p v_{p} vp, u q u_{q} uq, v q v_{q} vq。请你根据给定的pattern 完成ORB 描述的计算。
提示：
- p, q 同样要做边界检查，否则会跑出图像外。如果跑出图像外，就设这个描述子为空。
- 调用cos 和sin 时同样请注意弧度和角度的转换。
computeORBDesc()
/**
* compute ORB descriptor
* @param [in] image the input image
* @param [in] keypoints detected keypoints
* @param [out] desc descriptor
*/
typedef vector<bool> DescType; // type of descriptor, 256 bools
void computeORBDesc(const cv::Mat &image, vector<cv::KeyPoint> &keypoints, vector<DescType> &desc) {
for (auto &kp: keypoints) {
DescType d(256, false);
for (int i = 0; i < 256; i++) {
// START YOUR CODE HERE (~7 lines)
if (kp.pt.x < 16 || kp.pt.y < 16 ||
kp.pt.x >= image.cols - 16 || kp.pt.y >= image.rows - 16) {
// d[i] = 0; // if kp goes outside, set d.clear()
d.clear();
break;
}
cv::Point2f p(ORB_pattern[i*4], ORB_pattern[i*4 + 1]);
cv::Point2f q(ORB_pattern[i*4 + 2], ORB_pattern[i*4 + 3]);
cv::Point2f pp = cv::Point2f(cos(kp.angle/180)*p.x - sin(kp.angle/180)*p.y,
sin(kp.angle/180)*p.x + cos(kp.angle/180)*p.y) + kp.pt;
cv::Point2f qq = cv::Point2f(cos(kp.angle/180)*q.x - sin(kp.angle/180)*q.y,
sin(kp.angle/180)*q.x + cos(kp.angle/180)*q.y) + kp.pt;
if(image.at<uchar>(pp.y, pp.x) < image.at<uchar>(qq.y, qq.x)){
d[i] = true;
}
// END YOUR CODE HERE
}
desc.push_back(d);
}
int bad = 0;
for (auto &d: desc) {
if (d.empty()) bad++;
}
cout << "bad/total: " << bad << "/" << desc.size() << endl;
// return;
}
代码输出：
2.3 暴力匹配
在提取描述之后，我们需要根据描述子进行匹配。暴力匹配是一种简单粗暴的匹配方法，在特征点不多时很有用。下面你将根据习题指导，书写暴力匹配算法。
所谓暴力匹配思路很简单。给定两组描述子P = [ p 1 p_{1} p1，…， p M p_{M} pM] 和Q = [ p 1 p_{1} p1，…， p N p_{N} pN]。那么，对P 中任意一个点，找到Q 中对应最小距离点，即算一次匹配。但是这样做会对每个特征点都找到一个匹配，所以我们通常还会限制一个距离阈值 d m a x d_{max} dmax，即认作匹配的特征点距离不应该大于 d m a x d_{max} dmax。下面请你根据上述描述，实现函数bfMatch，返回给定特征点的匹配情况。实践中取 d m a x d_{max} dmax = 50。
提示：
- 你需要按位计算两个描述子之间的汉明距离。
- OpenCV 的DMatch 结构，queryIdx 为第一图的特征ID，trainIdx 为第二个图的特征ID。
- 作为验证，匹配之后输出图像应如图2 所示。
图2: 匹配图像
bfMatch（）
/**
* brute-force match two sets of descriptors
* @param desc1 the first descriptor
* @param desc2 the second descriptor
* @param matches matches of two images
*/
void bfMatch(const vector<DescType> &desc1, const vector<DescType> &desc2, vector<cv::DMatch> &matches) {
int d_max = 50;
// START YOUR CODE HERE (~12 lines)
// find matches between desc1 and desc2.
for (int i1 = 0; i1 < desc1.size(); ++i1) {
if(desc1[i1].empty()){
continue;}
cv::DMatch match(i1, 0, 256);
for (int i2 = 0; i2 < desc2.size(); ++i2) {
if(desc2[i2].empty()){
continue;}
int distance = 0;
for (int j = 0; j < 256; ++j) {
if(desc1[i1][j] != desc2[i2][j]){
distance++;
}
}
if(distance < d_max && distance < match.distance){
match.distance = distance;
match.trainIdx = i2;
}
}
if(match.distance < d_max){
matches.push_back(match);
}
}
// END YOUR CODE HERE
for (auto &m: matches) {
cout << m.queryIdx << ", " << m.trainIdx << ", " << m.distance << endl;
}
// return;
}
代码输出：
完整代码
最后，请结合实验，回答下面几个问题：
1. 为什么说ORB 是一种二进制特征？
答：因为ORB所用的Brief描述子采用的是0和1二进制表示。
2. 为什么在匹配时使用50 作为阈值，取更大或更小值会怎么样？
答：取更大值可能会有更多误匹配，取更小值则匹配得到的点会减少。
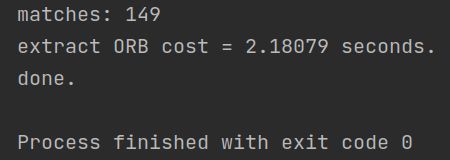
3. 暴力匹配在你的机器上表现如何？你能想到什么减少计算量的匹配方法吗？
答： VMware虚拟机用时: 2.18s， 可以通过限制match的范围来避免对keypoints2所有结果的多次遍历
3 从 E 恢复 R, t
我们在书中讲到了单目对极几何部分，可以通过本质矩阵E，得到旋转和平移R, t，但那时直接使用了OpenCV 提供的函数。本题中，请你根据数学原理，完成从E 到R, t 的计算。程序框架见code/E2Rt.cpp.
设Essential 矩阵E 的取值为（与书上实验数值相同）：
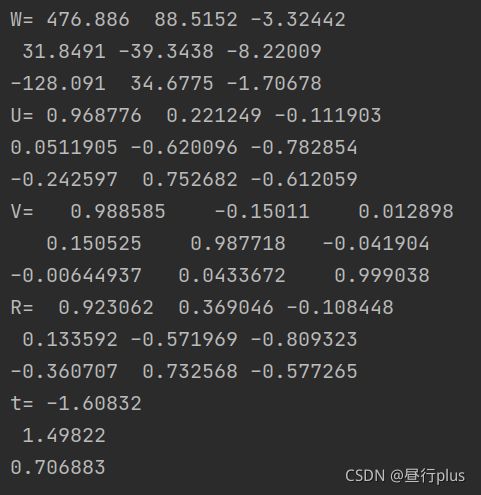
请计算对应的R; t，流程如下：
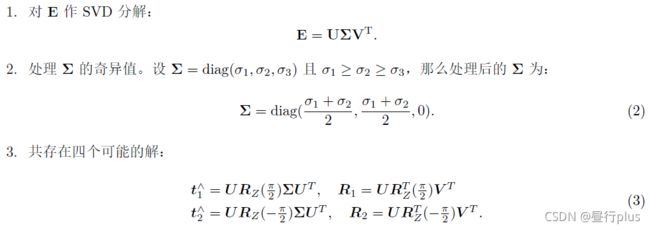
- 其中U是n×n正交阵，V是p×p正交阵， Σ \Sigma Σ是n×p实正矩阵，其主对角线外为零；
- Σ \Sigma Σ的对角线项称为E的奇异值，U和V分别称为E的左奇异向量和右奇异向量。
- R Z ( π 2 ) R_{Z}(\frac{\pi }{2}) RZ(2π)表示沿Z 轴旋转90 度得到的旋转矩阵。
同时，由于-E 和E 等价，所以对任意一个t 或R 取负号，也会得到同样的结果。因此，从E 分解到t，R 时，一共存在四个可能的解。请打印这四个可能的R, t。
提示：用AngleAxis 或Sophus::SO3 计算 R Z ( π 2 ) R_{Z}(\frac{\pi }{2}) RZ(2π)。
注：实际当中，可以利用深度值判断哪个解是真正的解，不过本题不作要求，只需打印四个可能的解即可。同时，你也可以验证t^R 应该与E只差一个乘法因子，并且与书上的实验结果亦只差一个乘法因子。
关于SVD的代码示例，可参考：http://eigen.tuxfamily.org/dox/classEigen_1_1JacobiSVD.html
E2Rt.cpp
//
// Created by daybeha on 2021/11/3.
// 本程序演示如何从Essential矩阵计算R,t
//
#include 代码输出：
4 用G-N 实现Bundle Adjustment 中的位姿估计
Bundle Adjustment 并不神秘，它仅是一个目标函数为重投影误差的最小二乘。我们演示了Bundle Adjustment 可以由Ceres 和g2o 实现，并可用于PnP 当中的位姿估计。本题，你需要自己书写一个高斯牛顿法，实现用Bundle Adjustment 优化位姿的功能，求出相机位姿。严格来说，这是Bundle Adjustment的一部分，因为我们仅考虑了位姿，没有考虑点的更新。完整的BA 需要用到矩阵的稀疏性，我们留到第七节课介绍。
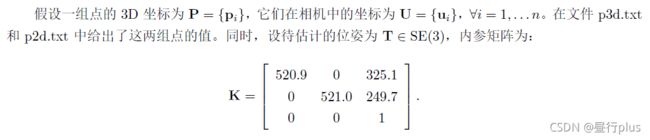
请你根据上述条件，用G-N 法求出最优位姿，初始估计为 T 0 T_{0} T0 = I。程序GN-BA.cpp 文件提供了大致的框架，请填写剩下的内容。
在书写程序过程中，回答下列问题：
1. 如何定义重投影误差？
答: e i = u i − 1 s i K e x p ( ξ ∧ ) P i e_{i} = u_{i} - \frac{1}{s_{i}} Kexp(\xi ^{\wedge})P_{i} ei=ui−si1Kexp(ξ∧)Pi
2. 该误差关于自变量的雅可比矩阵是什么？
至于公式②怎么来的，可以参考高博的《视觉SLAM十四讲》第二版，p85-86, SE(3)上的李代数求导
3. 解出更新量之后，如何更新至之前的估计上？
答：左乘exp(dx),扰动模型
对应代码：T_esti = Sophus::SE3d::exp(dx) * T_esti;
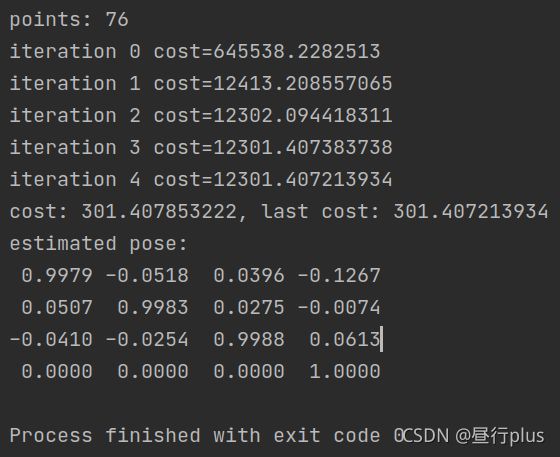
作为验证，最后估计得到的位姿应该接近：
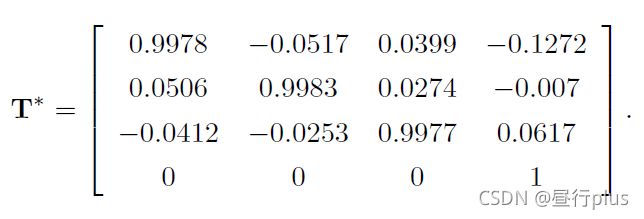
这和书中使用g2o 优化的结果很接近。
但是书中由于代码中错误地设置了depth scale（应该为5000，实际输入了1000），所以应该说和修正后结果相近。
高斯牛顿公式： J T J Δ x = − J T ∗ e J^{T}J\Delta x= -J^{T}*e JTJΔx=−JT∗e
GN-BA.cpp
//
// Created by daybeha on 2021/11/3.
//
#include 代码输出：
5 * 用ICP 实现轨迹对齐
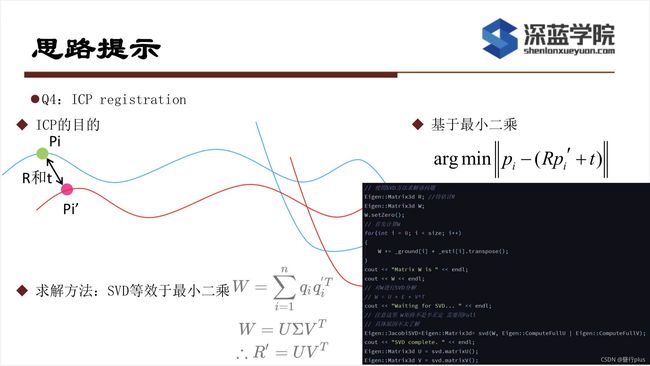
在实际当中，我们经常需要比较两条轨迹之间的误差。第三节课习题中，你已经完成了两条轨迹之间的RMSE 误差计算。但是，由于ground-truth 轨迹与相机轨迹很可能不在一个参考系中，它们得到的轨迹并不能直接比较。这时，我们可以用ICP 来计算两条轨迹之间的相对旋转与平移，从而估计出两个参考系之间的差异。
图3: vicon 运动捕捉系统，部署于场地中的多个红外相机会捕捉目标球的运动轨迹，实现快速定位。
设真实轨迹为 T g T_{g} Tg，估计轨迹为 T e T_{e} Te，二者皆以 T W C T_{WC} TWC 格式存储。但是真实轨迹的坐标原点定义于外部某参考系中（取决于真实轨迹的采集方式，如Vicon 系统可能以某摄像头中心为参考系，见图3），而估计轨迹则以相机出发点为参考系（在视觉SLAM 中很常见）。由于这个原因，理论上的真实轨迹点与估计轨迹点应满足：
其中i 表示轨迹中的第 i 条记录， T g e T_{ge} Tge ∈ SE(3) 为两个坐标系之间的变换矩阵，该矩阵在整条轨迹中保持不变。 T g e T_{ge} Tge可以通过两条轨迹数据估计得到，但方法可能有若干种：
-
认为初始化时两个坐标系的差异就是 T g e T_{ge} Tge，即：
-
在整条轨迹上利用最小二乘计算 T g e T_{ge} Tge：
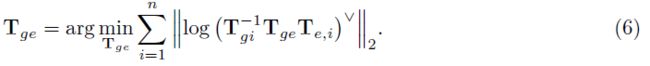
3. 把两条轨迹的平移部分看作点集，然后求点集之间的ICP，得到两组点之间的变换。
其中第三种也是实践中用的最广的一种。现在请你书写ICP 程序，估计两条轨迹之间的差异。轨迹文件在compare.txt 文件中，格式为：
time, t, q的具体格式：
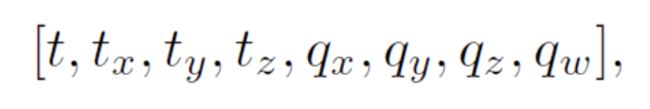
其中t 表示平移，q 表示单位四元数。请计算两条轨迹之间的变换，然后将它们统一到一个参考系，并画在pangolin 中。轨迹的格式与先前相同，即以时间，平移，旋转四元数方式存储。
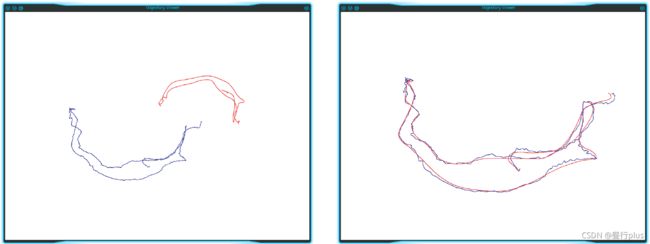
本题不提供代码框架，你可以利用之前的作业完成本题。图4 显示了对准前与对准后的两条轨迹。
图4: 轨迹对准前与对准后
黑熊助教思路提示：
//
// Created by daybeha on 9/11/2021.
//
#include 代码输出：
对准前：
对准后：
参考：
https://www.cnblogs.com/meteoric_cry/p/7987548.html
http://eigen.tuxfamily.org/dox/classEigen_1_1JacobiSVD.html
https://blog.csdn.net/weixin_41074793/article/details/85133424
https://blog.csdn.net/weixin_44218240/article/details/105924752?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_41074793/article/details/85133424
https://github.com/gaoxiang12/slambook2