《动手学深度学习》基础篇

摘要

入坑深度学习，从沐神开始，看过一遍视频后重新回头啃代码。对原来一知半解的地 方仔细思考，增加了一些注释。对内容进行了精简化。适合复习。其中的主要代码进行了合并验证，可以在jupyter运行。

前言

深度学习需要同时理解：

1. 问题的动机和特点；
2. 将大量不同类型的神经网络层通过特定的方式组合在一起的模型背后的数学原理；
3. 在原始数据上拟合极复杂的深层模型的优化算法；
4. 有效训练模型、避免数值计算陷阱以及充分利用硬件性能所需的工程技能；
5. 为解决方案挑选合适的变量（超参数）组合的经验；

本书的学习社区、免费教学资源（课件、教学视频、更多习题等），以及用于本书学习或教学的免费计算资源（仅限学生和老师）的申请方法在本书网站 https://zh.d2l.ai 上发布。

“纸上得来终觉浅，绝知此事要躬行。” —— 陆游

如何使用本书

附录中提供了本书所涉及的主要数学知识。中文教程 http://www.runoob.com/python/python-tutorial.html 英文教程 http://learnpython.org/

内容和结构

• 第一部分（1-3章）：预备工作、基础知识。第一章：深度学习背景；第二章：预备知识；第三章：基础概念和技术
• 第二部分（4-6章）：现代深度学习技术。第四章：深度学习各个重要组成部分；第五章：卷积神经网络；第六章：处理序列数据的循环神经网络。
• 第三部分（7-10章）：计算性能和应用。第七章：优化算法；第八章：影响计算性能的几个重要因素；第九章：计算机视觉的应用；第十章：自然语言处理的应用。

下图1：

书的网站是 https://zh.d2l.ai ，学习社区地址（https://discuss.gluon.ai/ ）和GitHub开源地址（https://github.com/d2l-ai/d2l-zh ）。
小伙伴们一定要多参加kaggle比赛练习练习哦！一起加油！！！

简介

机器学习和深度学习应用共同的核心思想：“用数据编程”。

我们可以收集一些已知包含猫与不包含猫的真实图像，然后我们的目标就转化成如何从这些图像入手得到一个可以推断出图像中是否有猫的函数。

这个函数的形式通常通过我们的知识来针对特定问题选定。例如，我们使用一个二次函数来判断图像中是否有猫，但是像二次函数系数值这样的函数参数的具体值则是通过数据来确定。

机器学习是一门讨论各式各样的适用于不同问题的函数形式，以及如何使用数据来有效地获取函数参数具体值的学科。深度学习是指机器学习中的一类函数，它们的形式通常为多层神经网络。

核心原则。

• 交替使用线性处理单元与非线性处理单元，它们经常被称为“层”。
• 使用链式法则（即反向传播）来更新网络的参数。

特点

机器学习研究如何使计算机系统利用经验改善性能。在机器学习的众多研究方向中，表征学习关注如何自动找出表示数据的合适方式，以便更好地将输入变换为正确的输出，深度学习是具有多级表示的表征学习方法。在每一级（从原始数据开始），深度学习通过简单的函数将该级的表示变换为更高级的表示。因此，深度学习模型也可以看作是由许多简单函数复合而成的函数。当这些复合的函数足够多时，深度学习模型就可以表达非常复杂的变换。
1. 深度学习可以逐级表示越来越抽象的概念或模式。
2. 端到端的训练.
3. 在自然语言处理领域，词袋模型多年来都被认为是不二之选。
4. 除端到端的训练以外，我们也正在经历从含参数统计模型转向完全无参数的模型。
5. 深度学习的不同在于：对非最优解的包容、对非凸非线性优化的使用，以及勇于尝试没有被证明过的方法。

预备知识

安装准备

win:

1. 安装Miniconda，在安装过程中需要勾选“Add Anaconda to the system PATH environment variable”选项（如当conda版本为4.6.14时）。
2. 下载包含本书全部代码的压缩包。我们可以在浏览器的地址栏中输入 https://zh.d2l.ai/d2l-zh-1.1.zip。再解压该文件，再从该文件夹下进入cmd命令模式。
3. 使用conda创建虚拟（运行）环境。conda和pip默认使用国外站点来下载软件，我们可以配置国内镜像来加速下载。

# 配置清华PyPI镜像（如无法运行，将pip版本升级到>=10.0.0）
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple

接下来使用conda创建虚拟环境并安装本书需要的软件。这里environment.yml是放置在代码压缩包中的文件。注意此时应任然处于d2l_zh文件夹下，该文件夹下有environment.yml文件。

conda env create -f environment.yml

4. 激活环境

conda activate gluon  # 若conda版本低于4.4，使用命令activate gluon

5. 打卡jupyter notebook。注意任然要先cd进d2l_zh文件夹下。

jupyter notebook

这时在浏览器打开 http://localhost:8888 （通常会自动打开）就可以查看和运行本书中每一节的代码了。

本书中若干章节的代码会自动下载数据集和预训练模型，并默认使用美国站点下载。我们可以在运行Jupyter记事本前指定MXNet使用国内站点下载书中的数据和模型（国外用户无须此操作）。

set MXNET_GLUON_REPO=https://apache-mxnet.s3.cn-north-1.amazonaws.com.cn/ jupyter notebook

mac/linux

1. 先下载miniconda，然后进入该下载文件夹，然后打开终端执行以下代码

# 以Miniconda官方网站上的安装文件名为准
sh Miniconda3-latest-Linux-x86_64.sh

安装时有以下问题：

Do you accept the license terms? [yes|no]
[no] >>> yes
Do you wish the installer to initialize Miniconda3
by running conda init? [yes|no]
[no] >>> yes

安装完成后，需要让conda生效。Linux用户需要运行一次source ~/.bashrc或重启命令行应用；macOS用户需要运行一次source ~/.bash_profile或重启命令行应用。

2. 下载本书代码压缩包，解压后进入该文件夹

mkdir d2l-zh && cd d2l-zh
curl https://zh.d2l.ai/d2l-zh-1.1.zip -o d2l-zh.zip
unzip d2l-zh.zip && rm d2l-zh.zip

3. 重复win。source deactivate退出虚拟环境。

更新代码和环境

第一步是重新下载最新的包含本书全部代码的压缩包。下载地址为 https://zh.d2l.ai/d2l-zh.zip 。解压后进入文件夹“d2l-zh”。

第二步是使用下面的命令更新运行环境：

conda env update -f environment.yml

使用GPU

1. 卸载CPU版本MXNet。如果没有安装虚拟环境，可以跳过此步。如果已安装虚拟环境，需要先激活该环境，再卸载CPU版本的MXNet。

pip uninstall mxnet

2. 更新依赖为GPU版本的MXNet。使用文本编辑器打开本书的代码所在根目录下的文件environment.yml，将里面的字符串“mxnet”替换成对应的GPU版本。例如，如果计算机上装的是8.0版本的CUDA，将该文件中的字符串“mxnet”改为“mxnet-cu80”。如果计算机上安装了其他版本的CUDA（如7.5、9.0、9.2等），对该文件中的字符串“mxnet”做类似修改（如改为“mxnet-cu75”“mxnet-cu90”“mxnet-cu92”等）。保存文件后退出。
3. 更新虚拟环境

conda env update -f environment.yml

数据操作

创建NDArray

from mxnet import nd  # 导入ndarray模块。简称nd
x = nd.arange(12)  # 创建一个0-11的12个元素的一维矩阵x
print (x.shape)  # 打印x的形状：12*1的矩阵
print (x.size)  # 打印x的元素个数。
X = x.reshape((3，4))  # 将12*1的矩阵x重新按照3*4排列为新的X矩阵
nd.zeros((2,3,4))  # 全0的2*3*4的矩阵
nd.ones((2,3))  # 全1的2*3矩阵
Y = nd.array([[1,2,3],[2,1,3],[3,2,1]])  # 通过list的方式直接指定Y为3*3的矩阵
nd.random.normal(0,1,shape=(3,4))  # 生成随机数。random均值为0 normal标准差为1 形状shape

运算

print (Y.exp())  # 对矩阵Y做指数运算
nd.dot(X , Y.T)  # 对矩阵X和Y的专制做乘法
nd.concat(X, Y, dim=0)  #对矩阵XY进行拼接增加行数
nd.concat(X, Y, dim=1)  #对矩阵X,Y拼接列数
X.sum()  # 对X中所有元素求和为一个元素nd.sum(X)
X.norm().asscalar()  # .asscalar对X的L2范数结果变为python中的标量  nd.norm(X)

广播机制

不同形状的矩阵进行运算时，会自动复制行或者列补充至一样的形状进行运算。

索引

X[1:3]  # 索引X矩阵的1，2两行，或数组中1，2两个元素
X[1,3] = 9  # 将X矩阵中1行3列（2，4）的元素替换为9
X[1:2, : ] = 9  # 将1行元素全部替换为9

运算的内存

Y = Y + X  # 更换内存地址
Y[:] = X + Y  # 只开临时地址，不更换地址
nd.elewise_add(X, Y, out=Y)  # 不开临时地址，不更换地址

NDArray和NumPy互相转换

D = nd.array(P)  # NumPy变NDArray
P = D.asnumpy()  # NDArray变NumPy

自动求梯度

# y = 2xTx
from mxnet import autograd, nd
x = nd.arange(4).reshape((4, 1))
x.attach_grad()  # 申请求梯度内存
with autograd.record():
	y = 2 * nd.dot(x.T, x)
y.backward()  # 自动求梯度

调用autograd函数后，记录求梯度函数，然后backward计算梯度。此外autograd函数还会将运行模式从预测模式转换为训练模式。

• 对Python控制流求梯度
  运算公式不是一个公式而是一个控制流程也能使用autograd自动求梯度

def f(a):
	b = a * 2
	# norm()对b平方求和再开方
	while b.norm().asscalar() < 100:
		b = b * 2
	if b.sum.asscalar() > 0:
		c = b
	else :
		c = 100 * b
	return c

a = nd.random.normal(0, 1, shape = (3, 3)) # 生成均值为0标准差为1的随机数
a.attach_grad()  # 申请求梯度内存
with autograd.record():
	c = f(a)
c.backward()

深度学习基础

线性回归

线性回归输出连续值，适合回归问题，例如预测房价、气温、销售额等连续值的问题。
softmax回归适用于分类问题，分类问题中模型最终输出值为离散值，例如图像分类，垃圾邮件识别，疾病监测等
线性回归和softmax回归都是单层神经网络。

线性回归基本要素

以预测房价为例解释线性回归。设房价取决于面积和房龄。

模型（model）：设面积为x1，房龄为x2，出售价格为y。

其中w1和w2是权重（wight），b是偏差（bias），且均为标量。他们是线性回归模型的参数（parameter）。y是真是价格，y‘是预测价格

模型训练(model training)

训练数据集（training data set）或训练集（training set）：多栋房屋的真实售价和对应的面积和房龄。（y,x1,x2）
一个样本（sample）：一栋房屋
标签（label）： 真实出售价格
特征（feature）： 预测标签的两个因素（房龄、面积）

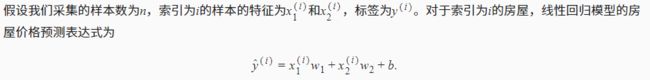
在机器学习中，衡量误差的函数称为损失函数（loss function）
损失函数：预测价格和真实价格的误差。常取非负数，数值越小误差越小。
常用误差函数：平方误差函数（square loss），他在评估索引为i的样本误差的表达式为：

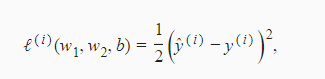
给定训练数据集，这个误差只与模型参数相关，因此将其记为以模型参数为参数的函数。
通常采用训练数据集中所有样本的平均误差来衡量模型预测的质量。即：

优化算法

通过小批量模型训练得出损失函数之后，有优化函数求梯度去优化模型的w1,w2,b得出更好的w1’,w2’,b’使误差变小。下一个batch_size训练时就会有更小的误差。最终得出最合适的w1’,w2’,b’

解析解（analytical solution）：当损失函数较为简单，上面的误差最小化问题的解可以直接用公式表达出来。（例如线性回归和平方误差）

数值解（numercial solution）：大多数深度学习模型没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数值。

小批量随机梯度下降（mini-batch stochastic gradient descent）：在求数值解的优化算法中，其在深度学习中被广泛使用。

小批量随机梯度下降：
1、选取一组模型参数的初始值，如随机选取。
2、对参数进行多次迭代，使每次迭代都可能降低损失函数值。在每次迭代中选取小批量（mini-batch）求数据样本中的平均损失有关模型参数的导数（梯度）。
3、用此结果与设定的一个正数（样本个数batch_size，学习率learning rate）的乘积作为模型参数在本次迭代的减少量。

超参数（hyperparameter）：小批量大小batch size ，学习率learning rate 。人为设定

调参：指调节超参数，反复试错。少数情况下超参数也可训练得出。

模型预测（模型推断、模型测试）

模型训练完后，将模型参数w1,w1,b在优化算法停止时的值分别记作w1’,w2’,b’。这里得到的不一定是最小化损失函数的最优解w1*,w2*,b*，而是对最优解的一个近似。然后用y=x1w1’ + x2w2’ + b’来估算训练出数据集以外的给定的任意移动面积为x1、房龄为x2的房屋价格。

线性回归的表示方法

解释线性回归与神经网路的联系，以及线性回归的矢量计算表达式

神经网络图

神经网络图省去了模型参数权重w1,w2和偏差b。输入x1,x2输出o。输入层的输入特征个数（特征向量维度）为2，输出个数为1。如果直接将神经网络图中的输出o作为线性回归的输出，即y’ = o。由于输出层不再进行下一步计算，所以图中神经网络层数为1。所以线性回归是一个单层的神经网络。输出层中负责计算o单元又叫神经元。

全连接层（fully-connected layer）或稠密层（dense layer）：输出层的神经元和输入层中各输入完全连接。

矢量计算表达式

在模型训练或预测时，常会同时处理多个数据样本并用到矢量计算。在介绍线性回归的矢量表达式之前，首先考虑对两个向量相加的两种方法。

from mxnet import nd
from time import time
# 定义两个1000维向量
a = nd.noes(shape=1000)
b = nd.ones(shape=1000)

# 将两个向量按元素逐一做标量加法。
start = time()
c = nd.zeros(shape=1000) # 初始化一个承载参数
for i in range(1000):
	c[i] = a[i] + b[i]
time() - start

# 将两个向量做矢量加法
start = time()
d = a + b
time() - start

结果是后者比前者更省时。结论：矢量计算更省时。矢量计算，向量直接相加。

线性回归利用NDArray、autograd实现

### 导入所需模块包
from mxnet import autograd , nd 
import random
import d2lzh

### 生成数据集。构造人工数据集，样本数1000，输入特征个数2，随机噪声e服从均值0，标准差0.01正态分布。
### 线性回归真实权重w=[2,-3.4]T和偏差b=4.2用来和训练出来的权重和偏差做对比。
### X随机生成的样本特征，是一个1000*2的矩阵，每一行第一个元素对应权重w1，第二个对应w2
### y = Xw + b + e
num_examples = 1000  # 输入样本个数
num_inputs = 2  # 输入单个样本的特征数
true_w = [2 , -3.4]  # 真实权重，用来和训练出来的权重系数做对比
true_b = 4.2  # 真实偏差
# 定义随机生成的样本特征features(X).  features:1000*2  labels:1*1000
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))

## 计算输出 y = Xw + b + e，这里注意噪音需分开计算
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b 
labels += nd.random.normal(scale=0.01, shape=labels.shape)
## 读取数据集,返回batch_size个随机样本的特征features和标签labels
def data_iter(batch_size, features, labels):
	num_examples = len(features)
	indices = list(range(num_examples))
	random.shuffle(indices)  # 样本特征随机打乱
	for i in range(0, num_examples, batch_size):
		j = nd.array(indices[i: min(i + batch_size, num_examples)])
		yield features.take(j), labels.take(j)  # take索引拿出对应元素
		
## 初始化参数模型
w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))  # 权重w是2*1的矩阵，每个样本特征x对应一个w
b = nd.zeros(shape=(1,))
w.attach_grad()  # 申请求梯度内存
b.attach_grad()

## 定义模型，返回模型计算值y
def linreg(X, w, b):
	return nd.dot(X, w) + b  # dot矩阵的乘法
	
## 定义损失函数[(y'-y)**2]/2。返回损失值y'-y
def squared_loss(y_hat, y):
	return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2  # reshape将真实值y变成和预测值y'一样的形状再相减
	
## 定义优化算法 小批量梯度下降，迭代模型优化损失函数。
## 一个batch_size的样本梯度平均数。返回新的param值
def sgd(params, lr, batch_size):
	for param in params:
		param[:] = param - lr * param.grad / batch_size ## grad求导函数
		
## 训练模型
lr = 0.03
num_epochs = 3
batch_size = 10
for epoch in range(num_epochs):  # 训练模型一共需要num_epochs个迭代周期
    # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）
    # X和y分别是小批量样本的特征和标签
    for X, y in data_iter(batch_size, features, labels):# 返回随机batch_size的features和labels传给X,y
        with autograd.record():
            l = squared_loss(linreg(X, w, b), y)  # squared_loss求出平方差损失函数
        l.backward()  # 对平方差损失函数参数求导
        sgd([w, b], lr, batch_size)  # 优化算法将batchsize中的每个样本产生的参数误差取平均数，并返回新的[w,b]
    train_l = squared_loss(linreg(features, w, b), labels) # 再用新的[w,b]带入公式求出y'，再和真实的y求出损失函数
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))

线性回归利用gluon实现

1、生成数据集
2、读取数据集
3、定义模型
4、初始化模型参数
5、定义损失函数
6、定义优化算法
7、训练模型

# 生成数据集
from mxnet import autograd ,nd
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + ture_b 
labels += nd.random.narmal(scale=0.01, shape=labels.shape)#features训练数据特征 labels标签
# 读取数据集，gluon提供data包读取数据，用gdata代替
from mxnet.gluon import data as gdata 
batch_size = 10
dataset = gdata.ArrayDataset(features, labels) # 将训练数据的特征和标签进行组合
data_ster = gdata.DataLoader(dataset, batch_size, shuffle=True)
# 定义模型。nn=nenural networks神经网络。先定义一个模型变量net，它是一个Sequential实例。在Gluon中，Sequential实例可以看作是一个串联各个层的容器。在构造模型时，我们在该容器中依次添加层。当给定输入数据时，容器中的每一层将依次计算并将输出作为下一层的输入。
from mxnet.gluon import nn
net = nn
net.add(nn.Dense(1))# 线性回归是单个全联接层，全连接层是Dense实例，输出个数1 
# 初始化模型参数。权重和偏差等。mxnet中的init（initializer）模块提供各种初始化方法。init.Normal(sigma=0.01)随机采样均值为0标准差0.01的正态分布，偏差默认初始化0
from mxnet import init
net.initialize(init.Normal(sigma=0.01))
# 定义损失函数。在gluon中定义了各种损失函数，用gloss代替liss
from mxnet.gluon import loss as gloss
loss = gloss.L2Loss() # 平方损失或L2范数损失
# 定义优化算法。导入gluon后创建Trainer实例，指定学习率为0.03的小批量随机梯度下降（sgd）优化算法。用来迭代net实例中所有通过add函数潜逃的层中全部参数。参数可通过collect_params函数获取
from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
     'learning_rate': 0.03})
# 训练模型。调用Trainer实例的step函数来迭代模型参数。l是长度为batch_size的一维NDArray，l.backward()等价于l.sum()backward()。按照sgd定义，在step函数中指明批量大小从而对批量中样本梯度求平均

softmax回归

分类模型，输出单元变成多个。

分类问题

输入图像高宽为2像素，色彩为灰度。每个像素都能用标量表示。将图像中四个像素记为x1,x2,x3,x4。假设训练集中图像真实标签为狗，猫或鸡（假设4个像素可以表示区分出3种动物），这些标签对应的离散值为y1,y2,y3。
通常使用离散的数值来表示类别，例如y1 = 1, y2 = 2, y3 = 3。如此，一张图像的标签为1，2和3其中的一个。

softmax分类模型

softmax回归同样将输入特征与权重做线性叠加。一共有4种特征和3种动物类别输出，softmax包含12个标量（w），3个偏差标量（b）

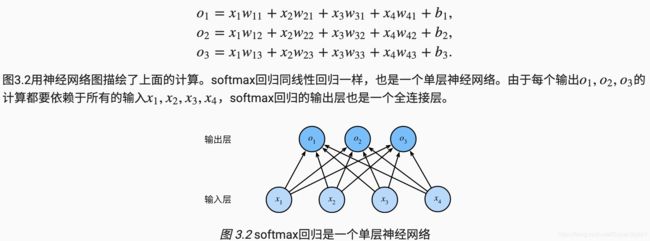
softmax运算

如果直接采用o1,o2,o3作为输出置信度，例如0.1， 10， 0.1，o2最大，所以预测为猫。如果为100，10，100等数值，范围不确定，也不好做判断。因此softmax运算符将o1,o2,o3转化为和为1的3个概率值有y’1,y’2,y’3。

交叉熵损失函数

使样本元素非1即0，类比于线性回归的平方差简化损失函数。数据集样本数n:

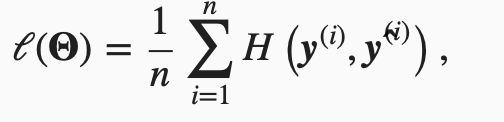
模型预测及评价

图像分类数据集（Fashion-MINIST）

1.获取数据集
2.读取小批量

%matplotlib inline 
import d2lzh as d2l
from mxnet.gluon import data as gdata
import sys
import time 
# 使用gluon的data获取训练数据集和测试数据集
mnist_train = gdata.vision.FashionMNIST(train=True) 
#训练集图像数6000，10个类别，60000个样本数
mnist_test = gdata.vision.FashionMNIST(train=False)
#测试集图像数1000，10个类别，10000样本数
#通过方括号[]来访问任意一个样本，下面获取第一个样本的图像和标签。
feature, label = mnist_train[0]
# 变量feature对应高和宽均为28像素的图像。每个像素的数值为0到255之间8位无符号整数（uint8）。它使用三维的NDArray存储。其中的最后一维是通道数。因为数据集中是灰度图像，所以通道数为1。为了表述简洁，我们将高和宽分别为 h 和 w 像素的图像的形状记为 h×w 或（h，w）。
feature.shape, feature.dtype
# 图像的标签使用NumPy的标量表示。它的类型为32位整数（int32）。
label, type(label), label.dtype
# 将数值标签转化为文字标签
def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]
#定义一个可以在一行里画出多张图像和对应标签的函数。
def show_fashion_mnist(images, labels):
    d2l.use_svg_display()
    # 这里的_表示我们忽略（不使用）的变量
    _, figs = d2l.plt.subplots(1, len(images), figsize=(12, 12))
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.reshape((28, 28)).asnumpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
#查看前9个样本的图像和文本标签
X, y = mnist_train[0:9]
show_fashion_mnist(X, get_fashion_mnist_labels(y))

# 读取小批量
#可通过yield定义小批量数据样本的函数，为了代码简洁，直接创建DataLoader实例。实例每次读取batch_size（一个超参数）的小批量数据。DataLoader可使用多进程加速数据读取。
batch_size = 500
transformer = gdata.vision.transforms.ToTensor() 
# ToTensor将图像数据从unit8格式变为32位浮点数，处以255将所有像素数值在0-1之间
# transform_first函数将ToTensor的变换应用在每个数据样本（图像和标签）的第一个元素
num_workers = 8 # 使用8进程读取
train_iter = gdata.DataLoader(mnist_train.transform_first(transformer), batch_size, shuffle=True, num_workers=num_workers)
test_iter = gdata.DataLoader(mnist_test.transform_first(transformer), batch_size, shuffle=True, num_workers=num_workers)

softmax从0实现

1、读取数据集
2、初始化模型参数
3、实现softmax运算
4、定义模型
5、定义损失函数
6、计算分类准确率
7、训练模型
8、预测

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, nd
#读取数据集
batch_size = 256 
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
#初始化参数模型
num_inputs = 784 #图像像素28*28=784
num_outputs = 10 #10个输出类别
W = nd.random.normal(scale=0.01, shape=(num_inputs, num_outputs))
b = nd.zeros(num_outputs)
W.attach_grad()
b.attach_grad()
#实现softmax运算
def softmax(X):
	X_exp = X.exp() #对X中每个元素做指数运算
	partition = X_exp.sum(axis=1, keepdims=True)
	#.sum(axis=1行求和=0列求和)，keepdims保留行列两个纬度
	return X_exp / partition #有广播机制
#定义模型
def net(X):
	return softmax(  nd.dot(X.reshape((-1, num_inputs)), W) + b)
	# y = WX + b
#定义交叉熵损失函数
def cross_entropy(y_hat, y):
	return -nd.pick(y_hat, y).log()
#计算分类准确率
	#.argmax返回最大值索引且返回值与y形状一样
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        y = y.astype('float32')
        acc_sum += (net(X).argmax(axis=1) == y).sum().asscalar()
        n += y.size
    return acc_sum / n
#训练模型
num_epochs, lr = 5, 0.1
def train_ch3(net, reain_iter, test_iter, loss, num_epochs, batch_size, params=None, lr=None, trainer=None):
	for epoch in range(num_epochs):
		train_l_sum, train_acc_sum, n = 0.0, 0.0, 0 # 初始化
		for X, y in train_iter:
			with autograd.record():
				y_hat = net(X)
				l = loss(y_hat, y).sum()
			l.backward()
			if trainer is None:
				d2l.sgd(params, lr, batch_size)
			else:
                trainer.step(batch_size)  # “softmax回归的简洁实现”一节将用到
            y = y.astype('float32')
            train_l_sum += l.asscalar()
            train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n += y.size
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
#预测
for X, y in test_iter:
    break
true_labels = d2l.get_fashion_mnist_labels(y.asnumpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1).asnumpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])

batch_size越大，迭代周期epochs就需要越大，反之越小。

softmax的gluon实现

%matplotlib inline
import d2lzh as d2l
from mxnet import gluon, init
from mxnet.gluon import loss as gloss, nn
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
net = nn.Sequential()  # 序贯模型
net.add(nn.Dense(10))  # 输出个数为10
net.initialize(init.Normal(sigma=0.01)) 
# 均值为0、标准差为0.01的正态分布随机初始化模型的权重参数。
loss = gloss.SoftmaxCrossEntropyLoss() #包括softmax运算和交叉熵损失计算的函数
#随机梯度优化算法
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
     'learning_rate': 0.1})
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None,
              None, trainer)

多层感知机

隐藏层

在输出层和输入层之间添加隐藏层。输入层不计算，计算隐藏层和输出层

添加隐藏层需要添加激活函数

激活函数

非线性函数变换
ReLu函数
只保留正元素。
sigmoid函数
将元素变换到0至1之间
tanh函数
将元素变换到-1至1之间

多层感知机

至少有一个隐藏层且每个隐藏层的输出通过激活函数变换。
多层感知机的层数和各隐藏层中隐藏单元中隐藏单元个数都是超参数
单隐藏层为例：

隐藏层做激活函数变换，输出层加入损失函数

多层感知机从0实现

1、读取数据集
2、定义模型参数
3、定义激活函数
4、定义模型
5、定义损失函数
6、训练模型

%matplotlib inline
import d2lzh as d2l
from mxnet import nd
from mxnet.gluon import loss as gloss
# 读取数据集
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 定义模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # hiddens中间层
W1 = nd.random.normal(scale=0.01, shape=(num_inputs, num_hiddens))
b1 = nd.zeros(num_hiddens)
W2 = nd.random.normal(scale=0.01, shape=(num_hiddens, num_outputs))
b2 = nd.zeros(num_outputs)
params = [W1, b1, W2, b2]
for param in params:
	param.attach_grad()
# 定义激活函数（使用基础的maximum）
def relu(X):
	return nd.maximum(X, 0)
# 定义模型
def net(X):
	X = X.reshape((-1, num_inputs))
	H = relu(nd.dot(X, W1) + b1)
	return nd.dot(H, W2) + b2
# 定义损失函数
loss = gloss.SoftmaxCrossEntropyLoss()
# 训练模型
num_epochs, lr = 5, 0.5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)

多层感知机的简洁实现

使用nd.add替代定义模型和模型参数

import d2lzh as d2l
from mxnet import gluon, init
from mxnet.gluon import loss as  gloss, nn
net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'), nn.Dense(10))
# 均值为0、标准差为0.01的正态分布随机初始化模型的权重参数。
net.initialize(init.Normal(sigma=0.01))
batch_size = 256 
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
loss = gloss.SoftmaxCrossEntropyLoss()
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
     'learning_rate': 0.5})
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, trainer)

模型选择、过拟合、欠拟合

训练误差：训练数据集时产生的误差
泛化误差：测试数据集表现出的误差
可通过损失函数计算两种误差
训练数据集，测试数据集
模型选择
验证数据集
训练数据集，测试数据集外
k折交叉验证
将原始训练数据集分为k个不同的子集，每次使用子集验证模型时，使用其他k-1个子集训练模型。最后求k次平均
欠拟合，过拟合
欠拟合：模型无法得到较低的训练误差，训练误差和测试误差都很大。（模型复杂度不够）
过拟合：训练误差远远小于测试误差。（模型复杂度过高）（增大数据集）
模型复杂度
高阶多项式复杂度高

权重衰减

过拟合，增大数据集困难时，采用权重衰减

方法

L2范数正则化，在模型损失函数基础上添加L2范数惩罚项——模型权重参数每个元素的平方和与一个正常数的乘积。

高维线性回归实验

使用特征数为200，均值0标准差0.01的线性函数
基础实现

%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import data as gdata, loss as gloss, nn
n_train, n_test, num_inputs = 20, 100, 200
true_w = nd.ones((num_inputs, 1)) * 0.01
true_b = 0.05
features = nd.random.normal(shape=(n_train + n_test, num_inputs))
labels = nd.dot(features, true_w) + true_b
labels += nd.random.normal(scale=0.01 , shape=(labels.shape))
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]

def init_params():
    w = nd.random.normal(scale=1, shape=(num_inputs, 1))
    b = nd.zeros(shape=(1,))
    w.attach_grad()
    b.attach_grad()
    return [w, b]
    
def l2_penalty(w):
    return (w**2).sum() / 2
    
batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss
train_iter = gdata.DataLoader(gdata.ArrayDataset(
    train_features, train_labels), batch_size, shuffle=True)
    
def fit_and_plot(lambd):
    w, b = init_params()
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with autograd.record():
                # 添加了L2范数惩罚项，广播机制使其变成长度为batch_size的向量
                l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
            l.backward()
            d2l.sgd([w, b], lr, batch_size)
        train_ls.append(loss(net(train_features, w, b),
                             train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features, w, b),
                            test_labels).mean().asscalar())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', w.norm().asscalar())

## 过拟合
fit_and_plot(lambd=0)
## 使用权重衰减
fit_and_plot(lambd=3)

###简洁实现
def fit_and_plot_gluon(wd):
    net = nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize(init.Normal(sigma=1))
    # 对权重参数衰减。权重名称一般是以weight结尾
    trainer_w = gluon.Trainer(net.collect_params('.*weight'), 'sgd',
                              {
     'learning_rate': lr, 'wd': wd})
    # 不对偏差参数衰减。偏差名称一般是以bias结尾
    trainer_b = gluon.Trainer(net.collect_params('.*bias'), 'sgd',
                              {
     'learning_rate': lr})
    train_ls, test_ls = [], []
    for _ in range(num_epochs):
        for X, y in train_iter:
            with autograd.record():
                l = loss(net(X), y)
            l.backward()
            # 对两个Trainer实例分别调用step函数，从而分别更新权重和偏差
            trainer_w.step(batch_size)
            trainer_b.step(batch_size)
        train_ls.append(loss(net(train_features),
                             train_labels).mean().asscalar())
        test_ls.append(loss(net(test_features),
                            test_labels).mean().asscalar())
    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
                 range(1, num_epochs + 1), test_ls, ['train', 'test'])
    print('L2 norm of w:', net[0].weight.data().norm().asscalar())
###

丢弃法

改善过拟合问题，除了权重衰减还可使用丢弃法（倒置丢弃法）
一定概率丢弃隐藏层层中的隐藏元素

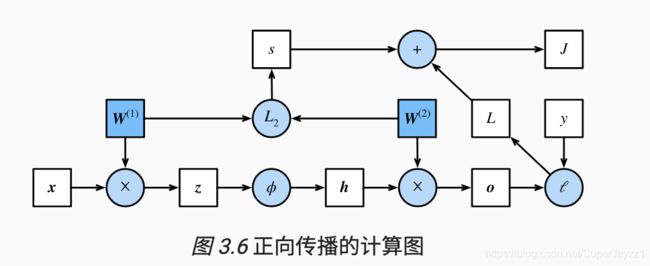
正向、反向传播

正向：

反向：求微分

数值稳定和模型初始化

神经网络层数较多时，模型数值稳定性容易变差，可能出现衰减或爆炸。
衰减：0.2的30次方约等于0
爆炸：2的30次方爆炸

随机初始化模型

在使用相同的激活函数，如果每个隐藏单元的参数都初始化为相同的值，那就等价于只有一个隐藏单元发挥作用。
MXNet的默认随机初始化
net.initialize(init.Normal(sigma=0.01))
使模型net的权重参数采用正态分布的随机初始化
net.initialize()
默认初始化，随机采样于-0.07到0.07之间的均匀分布，偏差参数为0
Xavier随机初始化
某全联接层的输入个数为a，输出个数为b，Xavier随机初始化将该层中权重参数的每个元素都随机采用与均匀分布，每层输出方差和梯度的方差不受输出个数影响