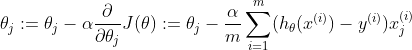机器学习实战（十四）Pegasos（原始估计子梯度求解器）

目录

0. 前言

1. SVM 概念

2. Pegasos

3. 实战案例

3.1. Pegasos

---

学习完机器学习实战的Pegasos，简单的做个笔记。文中部分描述属于个人消化后的理解，仅供参考。

本篇综合了先前的文章，如有不理解，可参考：

机器学习实战（五）支持向量机SVM

吴恩达机器学习（十）支持向量机

机器学习实战（四）逻辑回归LR

所有代码和数据可以访问 我的 github

如果这篇文章对你有一点小小的帮助，请给个关注喔~我会非常开心的~

0. 前言

Pegasos（primal estimated sub-gradient solver for SVM），支持向量机的原始估计子梯度求解器。

Pegasos 是一种通过随机梯度下降求解 SVM 的分隔超平面的方法。

研究表明，该算法所需的迭代次数取决于用户所期望的精确度而不是数据集大小。

1. SVM 概念

如下图所示（图源：百度百科）， 为分割超平面，在超平面上下方各建立一个界面  和  ，在  之上的为一类，在  之下的为一类。SVM的目的是为了最大化间隔，即  到  的距离：

在SVM中，定义正类  ，定义反类  ，这是为了方便后面计算。

通过  拟合数据的分界线，即超平面，则可定义上界面为  ，下界面为  。因可以通过改变系数的倍数表示距离，所以可粗略定义为  。

上界面以上的点表示为  ，下界面以下的点表示为  ，所以综合可得  。

在之前的文章中，求解 SVM 的超平面使用到了拉格朗日乘子法、KKT条件以及SMO序列最小优化。

在本篇中，将从梯度下降的角度求解 SVM 的超平面，即 Pegasos 算法。

2. Pegasos

在逻辑回归中，使用  定义分隔面，再套一层 sigmoid ，使用梯度下降求解分隔面。

换个角度理解 SVM ，在 SVM 中，也使用  定义分隔面，只是要求更加严格，增加了一个上平面和下平面，一个类别只能在上（下）平面之上（下）才符合要求，然后使用梯度下降求解分隔面。

可将梯度下降的代价函数粗略表示如下：

当  时，即 cost1，若  ，则满足  的条件（不考虑  ， 可用  代替），则代价函数为  ，不需要进行梯度下降。当  时，即 cost2，若 ，则满足  的条件，则代价函数为  ，不需要进行梯度下降。

否则，进行梯度下降，代价函数表示为：

不论  还是  ，距离此平面越远，代价函数越大，根据梯度下降公式：

可以等效如下：

若采用批量的随机梯度下降，则表示如下：

Pagasos 算法的流程表示如下：

3. 实战案例

以下将展示书中案例的代码段，所有代码和数据可以在github中下载：

3.1. Pegasos

# coding:utf-8
from numpy import *
import matplotlib
import matplotlib.pyplot as plt

"""
Pegasos: 支持向量机的原始估计子梯度求解器
primal estimated sub-gradient solver for SVM
"""


# 加载数据集
def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


# 线性预测
def predict(w, x):
    return w * x.T


# pegasos 随机梯度下降
# 1次只选择1个样本
def seqPegasos(dataSet, labels, lam, T):
    m, n = shape(dataSet)
    w = zeros(n)
    # 迭代T次
    for t in range(1, T + 1):
        i = random.randint(m)
        eta = 1.0 / (lam * t)
        p = predict(w, dataSet[i, :])
        # 不满足SVM要求
        if labels[i] * p < 1:
            w = (1.0 - 1 / t) * w + eta * labels[i] * dataSet[i, :]
        else:
            w = (1.0 - 1 / t) * w
    return w


# pegasos 随机梯度下降
# 1次只选择k个样本
def batchPegasos(dataSet, labels, lam, T, k):
    m, n = shape(dataSet)
    w = zeros(n)
    dataIndex = arange(m)
    # 迭代T次
    for t in range(1, T + 1):
        wDelta = mat(zeros(n))
        eta = 1.0 / (lam * t)
        random.shuffle(dataIndex)
        for j in range(k):
            i = dataIndex[j]
            p = predict(w, dataSet[i, :])
            # 不满足SVM要求
            if labels[i] * p < 1:
                wDelta += labels[i] * dataSet[i, :].A
        # 取k次的平均
        w = (1.0 - 1 / t) * w + (eta / k) * wDelta
    return w


if __name__ == '__main__':
    datArr, labelList = loadDataSet('testSet.txt')
    datMat = mat(datArr)
    # finalWs = seqPegasos(datMat, labelList, lam=2, T=5000)
    finalWs = batchPegasos(datMat, labelList, lam=2, T=50, k=100)
    print(finalWs)

    fig = plt.figure()
    ax = fig.add_subplot(111)
    x1 = []
    y1 = []
    xm1 = []
    ym1 = []
    # 区分两个类别
    for i in range(len(labelList)):
        if labelList[i] == 1.0:
            x1.append(datMat[i, 0])
            y1.append(datMat[i, 1])
        else:
            xm1.append(datMat[i, 0])
            ym1.append(datMat[i, 1])
    ax.scatter(x1, y1, marker='s', s=90)
    ax.scatter(xm1, ym1, marker='o', s=50, c='red')
    x = arange(-6.0, 8.0, 0.1)
    y = (-finalWs[0, 0] * x - 0) / finalWs[0, 1]
    ax.plot(x, y, 'g-')
    ax.axis([-6, 8, -4, 5])
    plt.show()

---

如果这篇文章对你有一点小小的帮助，请给个关注喔~我会非常开心的~