机器学习——入门基础
文章目录
- 西瓜书机器学习第二章
-
- 模型评估和选择
-
- 一种训练集一种算法
-
- 模型的评估方法
- 性能度量值
- 一种训练集多种算法
-
- P-R曲线
- ROC曲线
- 多种训练集一种算法
-
- 代价敏感错误率和代价曲线
- 测试集上的性能在多大程度上可以保证真实的性能
-
- 比较检验
-
- 一个测试集一种算法
- 假设检验
- 多个测试集一种算法
西瓜书机器学习第二章
数据、某种学习算法、模型、预测
科学推理的手段:归纳(特殊到一般)、演绎(一般到特殊)
训练出了不同模型,怎么选择?选最简单的
贴上宝藏up主的传送门致敬大神的个人空间_哔哩哔哩_bilibili
模型评估和选择
一种训练集一种算法
案例1:拿识别图片中的数字举例,比如每张图片中有一个数字
表1
| 字母/特殊含义 | 含义 | 实际案例 |
|---|---|---|
| m | 样本的数量 | 多少张图片 |
| Y | 正确的结果 | 比如第一张的正确结果是1,第二张是7 |
| Y’ | 模型预测出的结果 | 算法模型推测出第一张是1 |
| a | 错误的数量 | 推测出的结果有a个错了 |
| 错误率E | E=a/m | |
| 精度accuacy | 1-E | |
| 误差error | |Y-Y’| |
模型的评估方法
测试集的保留方法
1、留出法:数据集三七分、二八分,但要注意训练集和测试集的分布情况(设想一种情况:假设金融业务10年数据你用前7年训练,后3年测试,难免后三年变化巨大,数据不准),所以在数据抽取方面考虑抽取数据的离散性,要均匀一点去取三七分(不过还是要看具体的业务场景,有的要拿历史数据预测将来变化)
2、k折交叉验证:K折就是将数据集拆分为k小块,验证集和测试集相互形成补集,循环的交替(形象理解,10折验证,将数据分为10份,每次取其中一份当作预测结果,其余九分为训练集,最后将每一次的结果取平均值)
3、自助法:就是采取随机抽样的方式(形象理解,10个数,1->10,每次有放回的随机取一个数,取了m次后,那必然有某个数每次被取的概率为1/m,不被取到概率为1-1/m,m次不被取到的概率为(1-1/m)m,当m趋向于无穷大,求极限可知该式子为e-1,约等于0.368),将每次抽取的数作为测试集,m次后没有抽到的数据作为测试集
验证集
验证集合主要是用于验证调参,因为很多参数一开始是人为指定的,需要不断的验证调这些参数值
最终的流程大致是:训练集——>验证集——>调参,过程循环,直到模型合格,再放到测试集上测试
性能度量值
案例2:给定一个数据的集合D=(x1,y1),(x2,y2)…(xm,ym),可以形象理解就是两个数,但是之前可能存在某种关系x1——>y1,然后利用某种算法模型,计算出f函数,对于每个x会产出一个f(x)值和x对应,比如现在的集合就是(2,3),(4,5),(7,1),f推导出2对应4,4对应5,7对应1,
均方误差,均方误差可以拆开理解,均是求和取平均,方是平方,误差就是计算f(x)和y值的误差值
错误率、精度,表1已经提及两个概念,下面公式的双竖杠就是一个判断条件,如果计算出的f(x)和y值不相同为1,相同为0
案例3:100个数,0或者1,二分,利用某个预测,结果中1为70,0为30,原来数据中1为60,0为40
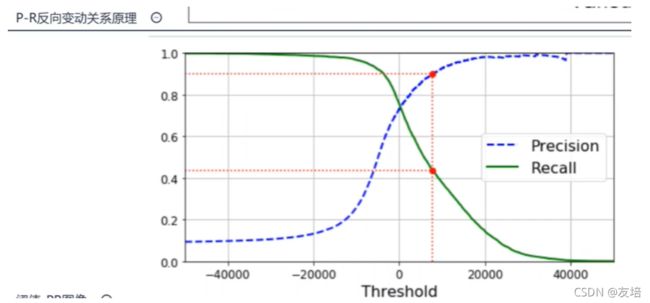
P查准率(准确率)、R查全率(召回率),代入上述案例,指标如下表,则查准率P=TP/(TP+FP),指的是在预测为正的基础上正确的所占比例,查全率R=TP/(TP+FN),指的是在原本为正的基础上预测出正的正确数所占比例,注意,其实在判断的时候会有一个界限,也就是标准,如果标准不高(范围较小)查准率会很高,查全率较低,这就是PR反向变动关系
表2
| 真实情况 | 预测为正(1)70 | 预测为反(0)30 |
|---|---|---|
| 正例(1) 60 | TP(真正例) 50 | FN(假反例) 10 |
| 反例(0) 40 | FP(假正例) 20 | TN(真反例) 20 |
那应该如何取阈值呢?
1、利用图中平衡点
2、F1度量,1/F1 = 1/2 * (1/p + 1/R)
3、Fbata(F1加权),1/Fb = 1/(1+b^2) * ( 1/p + (b^2)/R ) ,简化后其实可以发现P的系数为1,R的系数为b^2,那当b>1的时候更注重R的影响,b<1的时候更注重P的影响
注意,上述的查准查全是在二分类的情况下,那如果多分分类呢?
假如就是要手写数字(1-10),要分成10类,那是有两种解决的办法
1、直接用某种算法
2、分解成多个二分类:
①、进行穷举两个数进行比较:1还是2、1还是3、…1还是10、2还是3…9还是10,那应该是要n*(n-1)/2种比较
②、进行穷举单个数和非单个数比较:1还是非1、2还是非2、…10还是非10,那应该是要n种比较
一种训练集多种算法
P-R曲线
按照前面一种训练集一种算法,算出每一种模型的PR曲线图
假设目前有A、B、C三种模型,那如何比较这三种模型的好坏呢?有三种方法
1、首先确定B肯定比C好,B包含C(在查全率相同的点,B的查准率大于等于C的查准率)。A和B可以比较面积(不容易推算)
2、比较F1
3、比较Fbeta
ROC曲线
参考上文表2二分,专有名词TPR=TP/(TP+FN),FPR=FP/(TN+FP),我们清楚为正的越多越好,为反的越少越好,但二者会同时增加,所以肯定选择TPR增大的时候,FPR增加的越缓越好,就是在相同TPR的时候,FPR越小越好
AUC
AUC就是ROC曲线下的面积,怎么算呢?引入rank loss
公式如下,公式不太好理解,可以形象理解,假设现在是有数字图片8 7 3 9 5 2 5 5 6 5 5 5,二分为5和非5,可知是5的个数为6,非5的个数也是6,我们将数从左到右编号,非5的从-1开始,5的从+1开始,那上述数字编号后为-1 -2 -3 -4 +1 -5 +2 +3 -6 +4 +5 +6,统计在每个 +数 右边的 -数数量,那就是+1为2,+2为1,+3为1,剩下为0,统计为4,再用4/(6 * 6)(6 * 6指的是之前统计的5和非5个数相乘),计算得4/36,这就是rank loss
那计算rank loss为了什么?因为AUC=1-rank loss
我们可以验证一下:8 7 3 9 5 2 5 5 6 5 5 5,以5和非5二分,阈值从右往逐层推进
表3
| 阈值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | 0/6 | 1/6 | 2/6 | 3/6 | 3/6 | 4/6 | 5/6 | 5/6 | 6/6 | 6/6 | 6/6 | 6/6 | 6/6 |
| FPR | 0/6 | 0/6 | 0/6 | 0/6 | 1/6 | 1/6 | 1/6 | 2/6 | 2/6 | 3/6 | 4/6 | 5/6 | 6/6 |
制作成图后,我们要计算的AUC就是蓝色区域面积,而黄色区域就是rank loss,那AUC=1-rank loss
多种训练集一种算法
代价敏感错误率和代价曲线
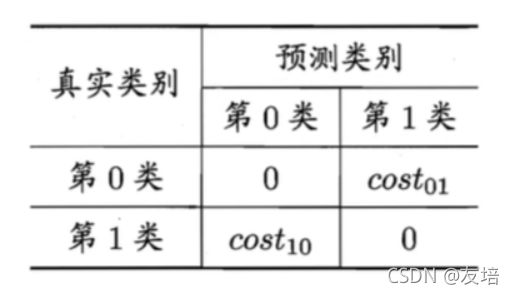
思考为什么引入这个计算,因为在很多时候不能仅仅依靠计算出上文提及的FNR和FPR,还得加上权重以及概率达到求取损失的期望,因而引入代价敏感错误率,下图为二分类代价矩阵
下图计算的是错误率error,可以看到分为两个集合正和负,双竖还是表示判断条件,m指的是总数
代价曲线的目的是为了根据给定模型的p值(m+/m, m+对应的是为正的数目,m-对应的是为反的数目),找到总的代价期望最小模型的阈值
代价曲线的纵轴是总期望cost norm,它的分子就是等于FNR * p * cost01 +FPR * (1-p) * cost10,分母可以先不考虑(其实是归一化,下文解释),所以最终的目的就是求p变化时总代价期望最小值;代价曲线的横轴是正概率的代价期望P+ cost ,它的分子为p * cost01;
设想一下为什么要除以分母,直接p——>FNR * p * cost01 +FPR * (1-p) * cost10,不就可以嘛?下文做解释
单个theta阈值
# python代码,单个theta阈值
import pandas as pd
# 函数输出打分
output_score = list(range(12))
# 正确分类
y = [0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1]
len(y)
# 设定p,集合种正例比例,范围是0-100,因此除以100
p = list(range(0, 101, 10))
p = [i / 100 for i in p]
# 设定代价值
c01 = 3
c02 = 2
# 设定阈值
theta = 6.5
# 函数输出判断
def calculate_output_result(output_score, theta):
output_result = []
for i in range(len(output_score)):
if output_score[i] < theta:
output_result.append(0)
else:
output_result.append(1)
return output_result
output_result = calculate_output_result(output_score, theta)
print(output_result)
# 统计正例反例的个数
def calculate_m_positive_negative(y):
result = pd.value_counts(y) # 分组统计次数
m_positive = result[1]
m_negative = result[0]
return m_positive, m_negative
m_positive, m_negative = calculate_m_positive_negative(y)
print(m_positive, m_negative)
# 计算混淆矩阵的TP、FN、FP、TN
def calculate_confusion(y, output_result):
con1 = 0
con2 = 0
con3 = 0
con4 = 0
for i in range(len(y)):
if y[i] == 1:
if y[i] == output_result[i]:
con1 += 1
else:
con2 += 1
else:
if y[i] == output_result[i]:
con4 += 1
else:
con3 += 1
return con1, con2, con3, con4
con1, con2, con3, con4 = calculate_confusion(y, output_result)
print(con1, con2, con3, con4)
# 求几个比例,保留四位小数
def calculate_FNR_FPR(con1, con2, con3, con4):
FNR = round(con2 / (con1 + con2), 4)
FPR = round(con3 / (con3 + con4), 4)
return FNR, FPR
FNR, FPR = calculate_FNR_FPR(con1, con2, con3, con4)
print(FNR, FPR)
# 正概率的代价
def calculate_Pcost(p, c01, c02):
Pcosts = []
for i in range(len(p)):
Pcost = round((p[i] * c01 / (p[i] * c01 + (1 - p[i]) * c02)), 4)
Pcosts.append(Pcost)
return Pcosts
Pcosts = calculate_Pcost(p, c01, c02)
print(Pcosts)
# 总代价
def calculate_cost_norm(p, c01, c02, FNR, FPR):
costs_nroms = []
for i in range(len(p)):
costs_nrom = round((FNR * (p[i] * c01) + FPR * (1 - p[i]) * c02) / (p[i] * c01 + (1 - p[i]) * c02), 4)
costs_nroms.append(costs_nrom)
return costs_nroms
costs_norm = calculate_cost_norm(p, c01, c02, FNR, FPR)
print(costs_norm)
# 画出图像
import matplotlib as mpl
import matplotlib.pyplot as plt
def plot_lines(X, Y, color):
plt.plot(X, Y, color)
return
plot_lines(Pcosts, costs_norm, 'r')
plot_lines(p, costs_norm, "b:")
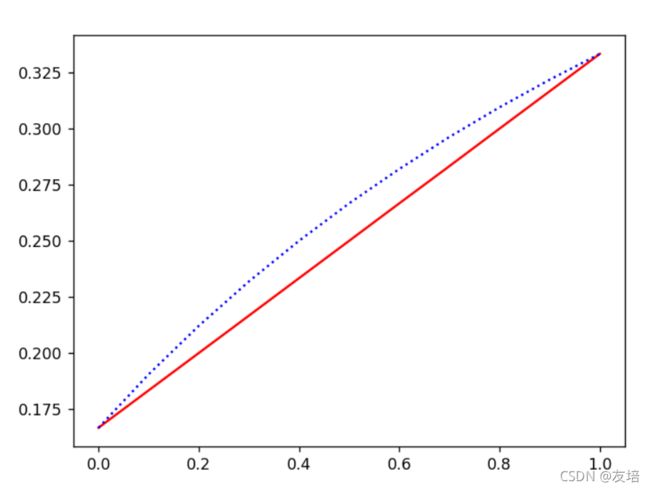
plt.show()
其实这里出图片后,我们不难看出,如果使用p作为x轴,那图像是一条曲线,而使用了归一化的正例概率代价,则图像是一条直线,显然线性的关系更容易分析
# python代码,多个theta阈值
thetas = list(range(12))
thetas = [i + 0.5 for i in thetas]
# 计算多个theta阈值对应的点的函数,并存在列表内
def calculate_Pcost_cost_norm(thetas, output_score, y, calculate_Pcost, calculate_cost_norm):
Pcosts_n = []
costs_norm_n = []
theta_FPR_FNR = {
}
for i in range(len(thetas)):
theta = thetas[i]
# 计算输出的结果
output_result = calculate_output_result(output_score, theta)
# 统计正例反例的个数
m_positive, m_negative = calculate_m_positive_negative(y)
# 计算混淆矩阵
con1, con2, con3, con4 = calculate_confusion(y, output_result)
# 求FNR FPR
FNR, FPR = calculate_FNR_FPR(con1, con2, con3, con4)
theta_FPR_FNR[theta] = [FNR, FPR]
# 正概率代价
Pcosts = calculate_Pcost(p, c01, c02)
Pcosts_n.append(Pcosts)
# 总代价
costs_norm = calculate_cost_norm(p, c01, c02, FNR, FPR)
costs_norm_n.append(costs_norm)
return Pcosts_n, costs_norm_n, theta_FPR_FNR
Pcosts_n, costs_norm_n, theta_FPR_FNR = calculate_Pcost_cost_norm(thetas, output_score, y, calculate_Pcost,
calculate_cost_norm)
for i in range(len(Pcosts_n)):
plot_lines(Pcosts_n[i], costs_norm_n[i], 'r')
plt.show()
测试集上的性能在多大程度上可以保证真实的性能
比较检验
一个测试集一种算法
二项分布概念,形象理解,1-10个数,判断每个数字为多少,假设判断错误的概率为0.3,正确的就为0.7,全部判断为错,就是下述公式中k=0,n=10,则全错的概率为(0.3^10) * (0.7^0)

# python实现二项分布
# 假设模型在全部数据上的错误率为0.3
e_all = 0.3
# 样本数量
m_T = 10
# 模型判断错误的数量
m_T_error = 6
# 模型在T上的错误率
e = round(m_T_error / m_T, 4)
# 出现这种情况的概率
from scipy.special import comb
def calculate_p(m_T, m_T_error):
# comb计算排列组合,对应的数学概率意义为C(k,n)
p = (comb(m_T, m_T_error)) * (e_all ** m_T_error) * ((1 - e_all) ** (m_T - m_T_error))
# 4位小数
p = round(p, 4)
return p
p = calculate_p(m_T, m_T_error)
print(p)
# 出现每种情况的概率
def calculate_ps(m_T):
m_T_errors = m_T_errors = list(range(m_T + 1))
ps = []
# 计算整体错误的概率
for i in range(len(m_T_errors)):
m_T_error = m_T_errors[i]
p = calculate_p(m_T, m_T_error)
ps.append(p)
return m_T_errors, ps
m_T_errors, ps = calculate_ps(m_T)
import matplotlib.pyplot as plt
def plot_scatter(x, y):
# s为大小,alpha为透明度
plt.scatter(x, y, s=20, c='b', alpha=0.5)
plt.show()
return
plot_scatter(m_T_errors, ps)
最终结果下图所示,不免发现错误数量等于3的时候概率最大
假设检验
假设检验的时候存在置信区间,形象理解,就是上面二项分布举例,比如我保证其90%可信度,就是超过90%两边不可信,最后错误的点落在了90%内那就保留,如果不在90%内那就不保留
现在假设错误率<=0.3,那其上限就是0.3,按照0.3的90%来算,下面代码计算出下标为5
def calculate_Ps(ps):
Ps = []
p = 0
for i in range(len(ps)):
p += ps[i]
Ps.append(p)
return Ps
Ps = calculate_Ps(ps)
# plot_scatter(m_T_errors, Ps)
import numpy as np
Ps_array = np.array(Ps) # array变成数组
confidence_indexs = np.argwhere(Ps_array > 0.9) # argwhere返回大于某个数的下标
confidence_index = confidence_indexs[0]
print(confidence_index)
# 结果为[5]
多个测试集一种算法
比如设想在k折交叉验证,会出现多个测试集,那就对应多个错误率,自然而然可以想到均值,也可以计算方差的指标
假设有三个测试集,每个测试集有0-10 11种情况,那总的情况就有11^3种,每种情况对应一个均值一个方差,均值和方差又满足某种关系。整体满足的就是t分布