我的机器学习/深度学习之路--LDA线性判别分析

关于LDA的理论方面，不过多赘述。只写一下我对这个算法的一些感想与验证过程。

只说二分分类问题：

数据采用(3条消息) 史上最好的LDA(线性判别分析)教程_jnulzl的专栏-CSDN博客_lda线性判别分析这篇博客的。这篇博客是用matlab验证的过程，我则用python验证的。

我认为二分分类问题中的LDA算法就是求得这个向量w，得到一个y的阈值，来判断测试集是否属于第1类或者第2类。但是这个y的阈值怎末求，我不知道，我看了许多关于LDA的博客，也只是说了说LDA的原理，也并没有说明这个y的阈值是什么，怎末求，我在这里姑且提出一种方法吧，不知道对不对，只是我个人的一点愚见。

  

 简单来说，就是取了训练集中两类数据投影到w里的距离y的最接近的两个值差的绝对值的平均，然后在加或减在这两个最接近值的其中一个中，就是确定的阈值yt。

下面是我用python验证：

数据：

#数据
print("数据")
X1=torch.tensor([[4,2],[2,4],[2,3],[3,6],[4,4]])
X2=torch.tensor([[9,10],[6,8],[9,5],[8,7],[10,8]])
print(X1)
print(X2)

均值矩阵：

#均值矩阵
u1=torch.zeros(1,2)
u2=torch.zeros(1,2)
for i in X1:
    u1+=i
for j in X2:
    u2+=j
u1=u1*1/len(X1)
u2=u2*1/len(X2)

协方差矩阵

#协方差矩阵
S1=torch.zeros(2,2)
S2=torch.zeros(2,2)
for i in X1:
    S1+=torch.mm((i-u1).T,(i - u1))
for i in X2:
    S2+=torch.mm((i-u2).T,(i - u2))
S1=S1*1/(len(X1)-1)
S2=S2*1/(len(X2)-1)
print("协方差矩阵")
print(S1)
print(S2)

类内散度矩阵 

#类内散度矩阵
print("类内散度矩阵")
Sw=S1+S2
print(Sw)

类间散度矩阵 

#类间散度矩阵
print("类间散度矩阵")
Sb=torch.mm((u1-u2).T,(u1-u2))
print(Sb)

求w*

#求w*
print("w")
Swni=torch.inverse(Sw)
w=torch.mm(Swni,(u1-u2).T)
print(w)
#归一化w
w=w/w.norm()
print(w)

求y=wtx

a=w[0,0].item()
b=w[1,0].item()
aaa=torch.zeros(1,2)
e0=[0,0,0,0,0]
e1=[0,0,0,0,0]
j=0
for i in X1:
    aaa=aaa+i
    #c=w.T*aaa
    d=torch.mm(w.T,aaa.T).item()
    e0[j]=d
    j=j+1
    aaa = aaa - i
j=0
for i in X2:
    aaa=aaa+i
    #c=w.T*aaa
    d = torch.mm(w.T, aaa.T).item()
    e1[j] = d
    j = j + 1
    aaa = aaa - i
print("y=wTX1")
print(e0)
print("y=wTX2")
print(e1)

 绘图

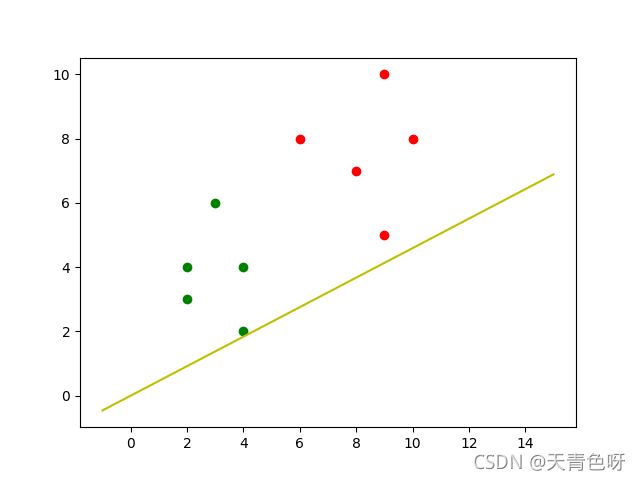
#X1与X2的散点图
plt.scatter(X2[:,0],X2[:,1],c = 'r')
plt.scatter(X1[:,0],X1[:,1],c = 'g')
#w直线
plt.plot([-1,15],[-1*b/a,15*b/a], color='y', linestyle='-')
plt.show()

 

 求阈值yt

#阈值yt
t=(1/2)*(min(e0)-max(e1))
yt1=max(e1)+t
yt2=min(e0)-t
print(yt1)
print(yt2)

由于时间关系，我并没有准备测试集以及验证分类准确率。