身为一个数学渣渣,每次用到基础定理时总得去百度……否则就会忘掉……很难受啊……所以写下一些基础数论以及一些证明,还有一些小模版,希望能帮助到一些和我一样瑟瑟发抖的小蒟蒻,若见大佬请多包含……如有错误也欢迎指出,此篇不定期更新。
目录
快速幂
欧几里得算法
扩展欧几里得
费马小定理
逆元
逆元+费马小定理
康托展开
矩阵乘法
后续
必须会的快速幂:
int pow(int a,int b){
int r=1,s=a;
while (b!=0){
if (b&1) r*=s;
s*=s;
b>>=1;
}
return r;
}
这个感觉不好解释吧……只能手动模拟了……这个只要知道怎么打就行了。
返回顶部
欧几里德算法:
gcd(a,b)=gcd(b,a%b);
已知a,b,求gcd(a,b)
int gcd(int a,int b){
if (b==0) return a;
return (b,a%b);
}
返回顶部
扩展欧几里德:
两个数a,b之间既然有最大公因数,则一定有x,y使一下等式成立
ax+by=gcd(a,b)
扩展欧几里德可以算出其x,y的值,以下为求法:
不妨设a>b;
当b=0时,可得gcd(a,b)=a。此时x=1,y=0;
当a>b>0时;
设ax1+by1=gcd(a,b);
bx2+(a%b)y2=gcd(b,a%b);
由欧几里德算法可得gcd(a,b)=gcd(b,a%b);
所以可得:ax1+by1=bx2+(a%b)y2;
即ax1+by1=bx2+(a-a/b*b)y2;
然后拆开来就可以得到:ax1+by1=bx2+ay2-(a/b)by2;
然后再合并就可以得到:ax1+by1=ay2+b(x2-(a/b)y2);
由恒等定理可得x1=y2,y1=x2-(a/b)y2;
所以x1和y1可以由x2和y2得出,可以用递归实现这个求解的过程;
以下为代码:
int gcd(int a,int b,int x,int y){
if (b==0){
x=1;y=0;
return a;
}
int r=gcd(b,a%b,x,y);
int t=x;x=y;y=t-a/b*y;
return r;
}
返回顶部
费马小定理:
设有整数a,质数p,且gcd(a,p)=1,则有a(p-1)≡1(mod p)
小小的证明:
一个数x的模p的集合有Q1={1,2,3,……,p-1};
再设一个集合Q2={a,2a,3a,……,(p-1)a};
可以由gcd(a,p)=1和质数p这两个条件得出Q2集合中的每一个元素都对应且唯一对应Q1中的的某一个元素,所以xa≡y(1<=x<=p-1,1<=y<=p-1)(mod p),由于p是质数,所以可以讲Q2中的每一个元素相乘与等式左边,Q1的每一个元素相乘与等式右边,以上等式仍然成立。所以可以得出:a*2a*3a*……*(p-1)a≡1*2*3*4*……*(p-1)(mod p)然后约分就可以得到费马小定理的等式:a(p-1)Ξ1(mod p)
返回顶部
逆元:
有a,m两个数设有x使得a*x≡1(mod m)则称x为a模m的逆元,在通常情况下写作1/a≡x(mod m),即(1/a)%m=x。
返回顶部
逆元+费马小定理:
a(p-1)≡1(mod p);
a(p-2)≡1/a(mod p);
所以当p是质数时可以得出a模p的逆元为a(p-2)。
有一个小例题,就是8月21号的考试T1,等一会儿写一下题解再贴一个链接。
◄传送门►
返回顶部
O(n)求1~n的逆元:
若是给你一个数n,要求求1~n所有数的逆元,用费马小定理的话效率是nlogn,还是有一点慢的。
因此我们需要一个O(n)的方法去求出1~n所有的逆元。
对于一个数x我们可以先设成t=P/x,k=P%x
那么就有t*x+k≡0(mod P)
两边移项可得-t*x≡k(mod P)
康托展开:
康托展开是求全排列顺序的一种公式,作用即为:给一个1~n的全排列,可以用公式求出这个全排列为所有全排列中的第几个全排列(从小到大),公式如下:
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[2]*1!+a[1]*0!
其中a[n]为在第n位的数字左边的没有出现过的并且比第n位数字小的数字的个数。代码如下:
#include
using namespace std;
long long n,a[100],tot;
long long m;
long long fact(long long n){
long long s=1;
for (long long i=2; i<=n; i++) s *=i;
return s;
}
long long tongji (long long x){
long long s=0;
for (long long i=1; i>n;
for (long long i=n; i>0; i--){
cin>>m;
a[m]=1;
tot=tot+tongji(m)*fact(i-1);
}
cout< 返回顶部
矩阵乘法:
讲真,矩阵乘法真的是一个困惑了我很久的东西,这个东西总是在各种地方被用到,但是每一次讲到矩阵乘法的时候我总是一脸蒙蔽,所以打算写一下关于矩阵乘法的东西(虽然并不知道这个是不是属于数论的东西)
首先先来理解一下矩阵乘法的基本描述:
设有两个矩阵分别为a,b,其中a是一个m*p的矩阵,b是一个p*n的矩阵。然后将两个矩阵相乘就是矩阵乘法了(废话)。当然在进行相乘时一定是根据一定规则的。设c=a*b。那么在c中的第i行第j列的元素可以用如下方式表达:
用比较通俗的语言来举个栗子,在C中的第一行的第一个(就是第一行第一列啦)元素就是A中的第一行与B中的第一列的每个对应元素的乘积的和。比如这样: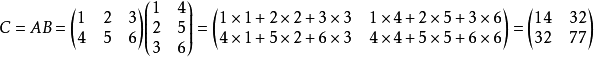
矩阵乘法的基本性质:
1.乘法结合律:(AB)C=A(BC)
2.乘法左分配律:(A+B)C=AC+BC
3.乘法右分配律:C(A+B)=CA+CB
4.对数乘的结合性k(AB)=(kA)B=A(kB)
5.转置(AB)T=BTAT
6.矩阵乘法一般不满足交换律
这样子讲了之后是不是明白了矩阵乘法究竟是什么呢?但是你是不是又发现,这个好像不知道有什么用诶……没错是的,之前我也不知道到底有什么用……所以接下来才是重点。
矩阵乘法+快速幂:
如果只是单纯的用矩阵乘法的话,效率其实是比正常的乘法效率要低很多。但是有一种奇妙的算法就是用矩阵乘法+快速幂。所以……这个东西到底有什么用呢。这么说吧,这个东西其实和动态规划的思想差不多。就是说,先用一个矩阵来表示第一个状态,然后,再有一个单元矩阵(怎么来的?慢慢试把少年。),设矩阵为a[n],单元矩阵为x。这个单元矩阵满足一下状态:a[i]*x=a[i+1],也就是说,用一个状态乘单元矩阵可以得到下一个状态,而最终要得到的是a[n],所以我们可以轻易的得出这个公式a[n]=a[1]*xn-1。然后我们可以先算这个xn-1(也就是用快速幂),再将a[1]乘上去。快速幂有多快大家是知道的……所以这样子效率可以大大提升。从而使得这个算法十分地快。
我会尽可能地去找一些例题的……但是个人感觉把……这个矩阵乘法这个东西比动态规划的思路来的还迷离,这个思路来的估计不会容易的……什么时候能够将例题题解发出来确实是一个值得令人思考的问题……
好吧,事实证明,已经过去好几天了,然而我还是没有写一个例题(这个初始矩阵真的是很难受),所以,写了一个模板以表歉意
◄传送门►
啊哈哈哈哈哈哈哈!我终于写了一个例题的题解!(当然是比较简单的矩阵乘法)
◄传送门►
另外,再附带上另一个博客的内容,是十个有关矩阵乘法的例题,有时间的话还是要一个一个做过来的,个人感觉挺有帮助的。
◄传送门►
返回顶部
数论篇后续:
全都写在一篇里面的话感觉会不会太挤,所以打算重新开一个吼。
基础数论Ⅱ——笑容渐渐消失
made by cain-