Policy Gradient 之 A3C 与 A2C 算法

Motivation

之前参加了学习强化学习以及PARL框架的训练营。这次是上次学习的一个拓展（“你学习，我送书，一起来爬RL的大山”）。这里主要来研究一下Policy Gradient下面的一个非常重要的算法A3C。

Background

Policy Gradient方法是对立于Value-based方法的另外一大类解决强化学习问题的算法。Policy Gradient下属有许多重要的算法，比如最基本的REINFORCE方法，以及Actor-Critic算法，PPO算法以及DDPG算法等。A3C在原始Actor-Critic的算法框架上加入了并行化模型的方法。最初在DeepMind在ICML2016年发表的论文Asynchronous Methods for Deep Reinforcement Learning中被提出。实际上，这篇论文不仅仅提出了A3C算法，还给出了一种在强化学习模型，特别是需要利用深度神经网络的深度强化学习模型中引入并行化方法的范式。论文中同样也给出了one-step Q-learning、one-step SARSA 以及 n-step Q-learning的并行化异步训练版本。

之所以要引进这样一种并行化训练的范式是因为在此前的强化学习算法中存在一些问题。因为agent与环境交互并得到reward以及下一个state这样的流程是一个串行的结构。如果我们希望充分利用历史经验来降低模型的variance以及减少环境扰动带来的偏差，我们就必须使用一个经验回放的机制。为此我们需要维护一个经验池。但是这样会导致占用巨大的存储空间以及我们的算法只能采用off-policy的方法。相信训练过DQN的同学都有这样的感受，训练一个简单的Atari模型就需要几十个小时，加上还要调参，可能一周时间也就跑几次实验，最后还是很难训练出来一个很好的模型。这也是强化学习算法难以复现的其中一个因素。另一方面，如果我们使用的是on-policy的方法，由于我们只能使用当前policy所生成的transaction作为训练数据，我们很难充分利用我们平时训练神经网络的时候采用的采样batch的方法来让我们的网络训练的比较稳定。所以这里就引入了一种并行化产生多个policy function同时探索并产生transaction数据来训练模型的想法。实际实验中我们会发现，增加了并行化之后，模型训练的速度直接起飞。比使用单机DQN快了好几倍。同时网络训练看起来也更加稳定。实际上在论文中作者也证实了这个结果:

First, we obtain a reduction in training time that is roughly linear in the number of parallel actor-learners. Second, since we no longer rely on experience replay for stabilizing learning we are able to use on-policy reinforcement learning methods such as Sarsa and actor-critic to train neural networks in a stable way.

在之后的实验中，大家发现异步更新和同步更新并不是决定算法优劣的主要因素，因此大家开始尝试非异步的方法，这样就有了A2C。接下来我们就从Policy Gradient开始，来理解一下A3C/A2C模型的结构以及背后的思想。之后再来看一下PARL里面是如何实现的。

Algorithm

Policy Gradient

首先我们还是来回顾一下Policy Gradient以及其中非常重要的一个基本算法：REINFORCE。与基于最优价值的强化学习算法不同，基于策略的强化学习算法并不对于值函数进行估计，而是直接输出action的参数或者action的概率从而计算策略可能更新的方向。Value-Based的方法是一种确定性策略，当模型优化到最优的时候，对于同样的一个state的输入，产生的action是确定的。Policy-based的策略可以表示随机性策略，这种策略在一些随机性较大的任务中效果更好。

强化学习的目标是最大化长期回报期望。由于环境和每一步动作都存在随机性，这里我们要先引入一个轨迹(Trajectory)的概念。我们将一个episode中出现的state和action的序列记为一个Trajectory：

$$\tau =\{s_1,a_1,s_2,a_2,..,s_T,a_T\}$$

该Trajectory发生的概率是：
$$p_{\theta }(\tau )=p(s_1){\pi }_{\theta }(a_1|s_1)p(s_2|s_1){\pi }_{\theta }(s_2|s_1,a_1)...$$

该Trajectory的总回报是：
$$R(\tau )=\sum _{t=1}^T{r}_t$$

当然我们知道，从一个state出发，之后会存在许多不同的Trajectories。故而，当前策略的期望回报就是所有轨迹的回报的期望。由于轨迹有很多，我们可以进一步采用蒙特卡洛法来近似估计这个期望回报，也就是通过所有episode的平均回报值来估计当前的策略的回报值：

$$J(\theta )={\bar{R}}_{\theta }=\sum _{\tau }R(\tau )p_{\theta }(\tau )\approx \frac{1}{N}\sum _{n=1}^{N}R(\tau )$$

我们采用梯度上升的方法来优化$J(\theta )$，进而通过计算$J(\theta )$关于$\theta$的梯度来更新$\theta$：$\theta \leftarrow \theta +\alpha {\nabla }_{\theta }{\bar{R}}_{\theta }$。${\nabla }_{\theta }J(\theta )$的梯度公式计算如下：
$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }\overline{R_{\theta }}\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n){\nabla }_{\theta }\log {\pi }_{\theta }(a_t^n|s_t^n)$$

进而我们可以得到一个loss函数：

$$\mathrm{L}=-R(\tau )\log {\pi }_{\theta }(a_t|s_t)$$

在具体实现的过程中，我们需要计算$R(\tau )$。这里面有两类不同的方法，一种是在一个episode结束之后再来计算，这也就是基于蒙特卡洛的方法，REINFORCE方法就是采用的这种思想；另一种是利用时序差分方法来计算，Actor-Critic系列的方法就是采用的这种思想。这里我们先列出其中比较简单的REINFORCE方法。Sutton书中的伪代码如下所示：

核心思想就是，首先按照当前策略生成一个trajectory。根据每个时间时刻所得到的reward值，计算每个时刻的return值(含衰减因子)，并用得到的return值更新策略参数。对于Loss function中的第二项，这里就是一个最大似然，我们可以理解为一个cross-entropy的项。这里面比较两个分布，一个是实际选取的action(用one-hot向量表示)，另一个是网络输出的每个action对应的值(概率)。和监督学习里面的多分类所不同的是，这里我们并不知道ground-truth，即我们并不知道当然所选取的action是不是最优的action。因为我们需要对其再增加一个置信度的系数，也就是之前我们所计算出来的return值。直观理解就是，如果当前action可以为我们带来更多收益，我们的网络就更应该朝着选择当前action的方向去更新。为了让模型能够收敛的更加稳定，这里还可以引入一个baseline项在叠加的reward之后，这里就不深入讨论了。

Actor-Critic

之前我们写出了REINFORCE中采用的$J(\theta )$，以及$J(\theta )$关于$\theta$的梯度。${\nabla }_{\theta }J(\theta )$的梯度公式计算如下：

$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }\overline{R_{\theta }}\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n){\nabla }_{\theta }\log {\pi }_{\theta }(a_t^n|s_t^n)$$

我们可以将其中的$R(\tau )$按照时序差分的方法来写出来。这样做的好处是可以通过牺牲一部分偏差来换取模型的方差减小。类似于我们在Q-learning中的做法，我们使用一个独立的模型来估计轨迹的长期回报，而不是直接使用轨迹的真实Return值。我们将$J(\theta )$关于$\theta$的梯度${\nabla }_{\theta }J(\theta )$的计算公式写出：

$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }\overline{R_{\theta }}\approx \frac{1}{T}\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^n|s_t^n)(r_{t+1}+v(s_{t+1})-v(s_t))$$

可以看到，这里的loss function是由policy和value两部分组成的。policy对应我们的Actor，value对应我们的Critic。贴一段Sutton书中的伪代码：

当然这里我们使用的是TD-error来估计$R(\tau )$，当然也有其他的方法可以来估计。从周博磊老师的Intro to RL的课件中我们可以看到这里有一系列方法来对应对于$R(\tau )$的改进:

A3C

终于要到A3C了。就像我们之前在Background里面讲的一样，由于Actor-Critic是on-policy的算法，我们在实际使用的时候不得不面对需要经常根据当前策略生成样本的需求，这就意味着我们需要花更多的时间和计算资源来生成和收集新样本。为了加快这部分的速度，一个非常直观的想法就是将这一部分变成并行化。在A3C中我们同时启动N个线程，每个线程内都有一个Agent与环境进行交互。只要保证每一个线程中的环境状态不同，线程之间的transaction就会不同，这样就达到了快速exploration的目的。在A3C中，每个线程在收集到样本之后回独立进行训练并更新模型参数，然后采用一种 Hogwild 的方法来异步的更新到总的全局模型上。当线程上的模型参数更新完成后进入下一个iteration，每个线程会和全局模型的参数进行同步。这就是A3C的总体结构。

这里有一些需要注意的地方。

1. 之前在AC算法中，我们利用单步的TD-error来估计当前的$R(\tau )$。这一部分的意义实际上是样本的权重，即我们更愿意保证总体收益更大的样本在我们的模型中可以获得一个小的loss。这样做固然可以让我们的模型变的更加稳定，但是同时也使得模型的偏差增加。很多时候，当前步的reward不仅仅对于当前的$Q(s,a)$有影响，还应当对多步之后的$s,a$对产生影响。单步更新的TD方法并不能很好的捕获这种关联关系。论文中也对这个问题进行了解释并给出了解决方法：

One drawback of using one-step methods is that obtaining a reward $r$ only directly affects the value of the state action pair $s$, $a$ that led to the reward. The values of other state action pairs are affected only indirectly through the updated value $Q(s,a)$. This can make the learning process slow since many updates are required the propagate a reward to the relevant preceding states and actions. One way of propagating rewards faster is by using n-step returns (Watkins, 1989; Peng & Williams, 1996). In n-step Q-learning, $Q(s,a)$ is updated toward the n-step return defined as $r_t+\gamma r_{t+1}+...+{\gamma }^{n-1}{r}_{t+n-1}+ma{x}_a{\gamma }^{n}Q(s_{t+n},a)$. This results in a single reward $r$ directly affecting the values of $n$ preceding state action pairs. This makes the process of propagating rewards to relevant state-action pairs potentially much more efficient.

也就是说A3C采用n-step TD来代替之前的单步TD-error，这也就是A3C(Asynchronous Advantage Actor-Critic)中的Advantage的意思。于是Actor-Critic算法中的目标函数的梯度就可以写成：

$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }\overline{R_{\theta }}\approx \frac{1}{T}\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^n|s_t^n)(\sum _{i=1}^n{\gamma }^{i-1}{r}_{t+1}+v(s_{t+n})-v(s_t))$$

至此，A3C的框架基本就形成了。论文中给出了这样的A3C对应的伪代码:

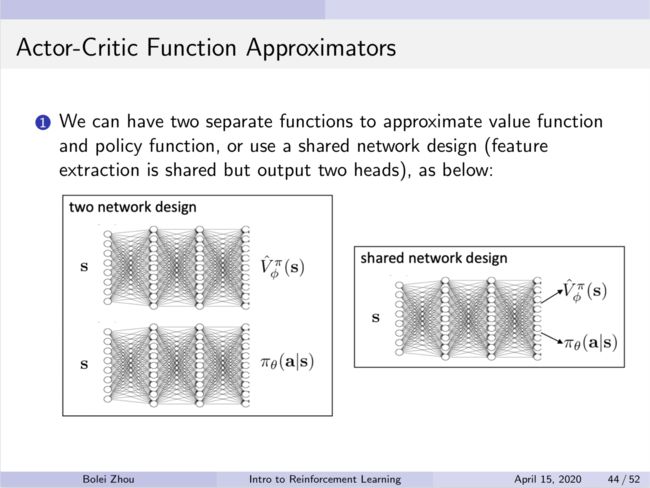
2. 在具体实现的过程中，我们的policy function和value function在特征提取的过程中是共用一部分神经网络的，这样可以减少总体的参数量同时增加模型的稳定性。还是从周博磊老师的slides里截取一个解释

3. 为了增加模型的探索性，防止其落入阶段性任务的局部最优中，模型的目标函数中又加入了策略的熵。由于熵表示的是概率分布的不确定性，所以如果模型的熵越大则代表其更有探索精神。论文中的阐述是:

We also found that adding the entropy of the policy $\pi$ to the objective function improved exploration by discouraging premature convergence to suboptimal deterministic policies. This technique was originally proposed by (Williams & Peng, 1991), who found that it was particularly helpful on tasks requiring hierarchical behavior.

至此，A3C模型的总体目标函数是：

$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }\overline{R_{\theta }}\approx \frac{1}{T}\sum _{t=1}^T{\nabla }_{\theta }\log \pi (a_t^n|s_t^n;\theta )(\sum _{i=1}^n{\gamma }^{i-1}{r}_{t+1}+v(s_{t+n})-v(s_t))+\beta {\nabla }_{\theta }\mathrm{H}(\pi (s_t;\theta ))$$

A2C

就像我们在前面说到的，Hogwild这种参数的更新方法与我们平时在深度学习中使用的方法不同，同时直觉上我们会怀疑这样的参数更新方法时候会对模型训练的效率产生负面的影响。实际上确实如此。不采用异步参数更新，只在每个线程中维持与环境的交互而将参数更新放在全局模型上的同步更新的方法效果更好且更加简洁，所以很多情况下我们使用的是A2C算法而非A3C算法。

Experiment

代码我在aistudio上贴了但是感觉有点占空间所以这里就不贴了，同学们可以去访问PARL库中对应的example来看 (A2C example)。说实话因为对于paddlepaddle框架的一些操作不是很熟悉再加上PARL对于很多类的封装比较深，有些地方的代码读起来不是很好理解。但是抛开源码，如果只是单纯使用的话，还是比较方便的。

Result

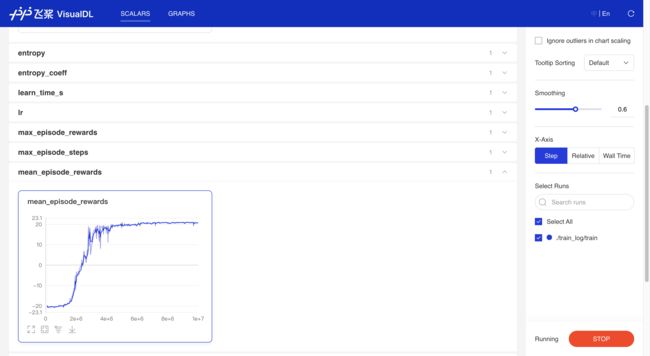
这里贴一个利用visualDL(paddle版的tensorboard)展示的训练结果。

可以看到模型可以在Pong的环境中很快收敛到20+的reward。

Remain Problems

1. xparl不是很稳定。我在aistudio上尝试在终端运行，除了前几次成功构建了cluster，后来都失败了，而且多次xparl stop之后，之前xparl start所使用的端口显示被占用。
2. 这里对于环境的包装比较复杂。我尝试了多种monitor环境的方法但是仍然不能在训练过程中存储某些episode的mp4文件。求大佬解决。

Reference

1. 周博磊_强化学习纲要
2. UCB CS285 Deep Reinforcement Learning
3. Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.
4. PARL
5. AI Studio Project