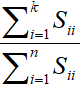基于k-means聚类图像分割+lbp+pca+svm实现烟雾识别(利用matlab仿真实现)
一、算法简介
1.1 c-means聚类算法
聚类分析是根据在数据中发现的描述对象及其关系的信息,将数据对象进行分组。目的是使组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。组内相似性越大,组间差距越大,说明聚类效果越好。
也就是说,聚类的目标是得到较高的类内相似度和较低的类间相似度,使得类间的距离尽可能大,类内样本与类中心的距离尽可能小。在此,我们选用k-means聚类算法。
1 .2 LBP算法
LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出,用于纹理特征提取,提取的特征是图像的局部的纹理特征。
原始的LBP算子定义为在3*3的窗口内,以窗口中心像素为阈值,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3*3邻域内的8个点经比较可产生8位二进制数(通常转换为十进制数即LBP码,共256种),即得到该窗口中心像素点的LBP值,并用这个值来反映该区域的纹理信息。
1.3 PCA算法
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。其算法步骤如下:
1)数据中心化——去均值,根据需要,有的需要归一化——Normalized;
2)求解协方差矩阵;
3)利用特征值分解/奇异值分解 求解特征值以及特征向量;
4)将特征值从大到小排序,保留前k个特征向量
5)利用特征向量构造投影矩阵;
6)利用投影矩阵,得出降维的数据。
1.4 SVM算法
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
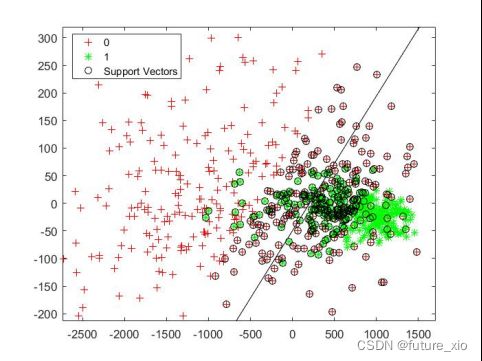
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示即为分类超平面,对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分类超平面却是唯一的。如下图1-1SVM算法示意图
图1-1SVM算法示意图
二、算法实现
2.1 烟雾识别算法流程
1)首先对所有图像进行预处理,假定将有烟当作正样本,将没烟看作负样本,train集的smoke文件夹改名为pos,train集的non文件夹改名为neg;同理将test集的smoke文件夹改名为pos,test集的non文件夹改名为neg。为了对所有图片进行处理,将train和test中的pos和neg中的图片全部规范命名格式为0001.jpg、0002.jpg、0003.jpg、0004.jpg、0005.jpg......。将这些图片名字提取出来分别存到“pos_list.txt、neg_list.txt、pos_test_list.txt、neg_test_list.txt文本中。如下图2-1图2-2所示
图2-1
图2-2
2)利用c-means聚类算法对训练集和测试集图像的像素进行聚类,实现图像分割。
3)利用LBP对分割后的训练集图像和测试集图像进行特征提取。
4)分别对训练集和测试集使用主成分分析法(PCA)进行特征降维。
5)利用对训练集降维后得到的二维特征训练SVM二分类模型,
6)最后利用对测试集降维后得到的二维特征进行分类预测。
整体算法流程如下图2-3所示
图2-3 算法流程框图
2.2 c-means算法实现
图像分割是利用图像的灰度、颜色、纹理、形状等特征,把图像分成若干个互不重叠的区域,并使这些特征在同一区域内呈现相似性,在不同的区域之间存在明显的差异性。然后就可以将分割的图像中具有独特性质的区域提取出来用于不同的研究。图像识别的基础是图像分割,其作用是把反映物体真实情况的、占据不同区域的、具有不同特性的目标区分开来,并形成数字特征。因此本文利用c-means聚类算法实现图像分割,实现对噪声的过滤,在构建烟雾识别模型的过程中,首先分别对无烟和有烟的图像进行c-means聚类图像分割。
本文对预处理过后的训练集和测试集图像进行像素聚类,在此分别列举一张有烟图和无烟图的图像分割前后的效果对比。如图2-4和图2-5所示
图2-4 无烟图像分割前后对照图
图2-5有烟图像分割前后对照图
2.3 LBP算法实现
本文LBP算法将像素聚类(3类)以后的图像进行特征提取。在此分别列举一张有烟图和无烟图的图像特征提取前后的效果对比。
图2-6无烟三像素聚类LBP特征提取前后对照图
图2-7有烟三像素聚类LBP特征提取前后对照图
本文PCA算法将HOG或LBP提取的特征进行特征降维,使数据可视化。PCA算法可以获取原有特征的大部分信息,降维以后的前k个特征值保留下来的信息占原有信息的比例可有下式计算获得。
对LBP算法提取的特征进行特征降维,在此取前两维特征进行模型训练,前两维度保留的信息含有98.75%,如下图2-8所示.
2.4 SVM算法实现
在经过上述图像预处理、图像像素聚类、LBP特征提取、PCA特征降维至两维过程之后,将二维特征向量作为输入训练SVM模型,最终得到模型在训练集上的分类准确度。
利用k-means+LBP+PCA+SVM算法,多次训练模型,最终取平均值,得到在训练集上的分类准确度为79%,在测试集上的分类准确度为78%。下图为模型在训练集上的分类效果图。
三、结果分析
经过第二章的算法实现,最终得到了完整的SVM二分类模型,利用该模型对test中的pos样本的图片和neg样本的图片进行预测。预测前,首先需要对测试集图片经过预处理、其次利用k-means3聚类法对像素进行聚类得到最终图像分割聚类图、然后对聚类图进行LBP特征提取、最后再利用PCA对提取出来的特征进行特征降维。将最终得到的二维特征向量作为模型的输入,进行分类预测,最终得到结果。对于LBP特征提取方法,在训练集和测试集上的准确率分别为79%和78%。经过对比可以发现模型的泛化性能良好。
最后笔者不得不提的是,之所以采取上诉方法实现烟雾识别是因为,大作业要求必须包含聚类、分类、降维。笔者也尝试过直接使用LBP+SVM实现烟雾识别的方法,并且对测试集的准确率可以达到93%。
这是两种不一样的解决问题的思路。若采用本文的思路是Pipeline,若直接采用LBP+SVM的思路叫做end2end,各有优缺点。Pipeline是将一个问题拆解成若干个子问题一次解决,然后串在一起,这种方法易于实现,且灵活性和可解释性更高,但缺点是多个子任务会造成错误累积。end2end是将一个问题看成一个整体,一般可以获得比pipeline更高的性能,但是整体像一个黑盒,可解释性差。现在深度学习最新研究的趋势是end2end的方法。
%基于LBP特征提取的主程序代码
clc;
clear ;
k = 2;
acc1 = 0;
acc2 = 0;
acc = 0;
%% 标签制作
ReadList1 = textread('pos_list.txt','%s','delimiter','\n');%载入正样本列表
sz1=size(ReadList1);
label1=ones(sz1(1),1); %正样本标签
ReadList2 = textread('neg_list.txt','%s','delimiter','\n');%载入负样本列表
sz2=size(ReadList2);
label2=zeros(sz2(1),1);%负样本标签
label_train = [label1',label2'];%训练集标签
ReadList_pos = textread('pos_test_list.txt','%s','delimiter','\n');%载入测试正样本列表
sz_pos=size(ReadList_pos);
label_pos=ones(sz_pos(1),1); %正样本标签
ReadList_neg = textread('neg_test_list.txt','%s','delimiter','\n');%载入测试负样本列表
sz_neg=size(ReadList_neg);
label_neg=zeros(sz_neg(1),1);%负样本标签
label_test = [label_pos',label_neg'];%测试集误差
total_trainnum=length(label_train);
total_testnum = length(label_test);
data1 = zeros(total_trainnum,256);
data2 = zeros(total_testnum,256);
%% 提取特征
%读取训练集正样本并计算lbp特征
for i=1:sz1(1)
name=char(ReadList1(i,1));
image1=imread(strcat('F:\模式识别matlab程序\模式识别大作业\yanwujiance\pos\',name));
I=double(image1)/255;
clu_kmeans=imkmeans(I,3);
clu_pic=clu_kmeans/3;
lbps = lbp(clu_pic);
data1(i,:)=lbps;
end
%读取训练集负样本并计算lbp特征
for j=1:sz2(1)
name= char(ReadList2(j,1));
image2=imread(strcat('F:\模式识别matlab程序\模式识别大作业\yanwujiance\neg\',name));
I=double(image2)/255;
clu_kmeans=imkmeans(I,3);
clu_pic=clu_kmeans/3;
lbps = lbp(clu_pic);
data1(sz1(1)+j,:)=lbps;
end
%读取测试集正样本并计算lbp特征
for m=1:sz_pos(1)
test_name= char(ReadList_pos(m,1));
image3=imread(strcat('F:\模式识别matlab程序\模式识别大作业\yanwujiance\test\pos_test\',test_name));
I=double(image3)/255;
clu_kmeans=imkmeans(I,3);
clu_pic=clu_kmeans/3;
lbpst= lbp(clu_pic);
data2(m,:)=lbpst;
end
%读取测试集负样本并计算lbp特征
for n =1:sz_neg(1)
test_name=char(ReadList_neg(n,1));
image4=imread(strcat('F:\模式识别matlab程序\模式识别大作业\yanwujiance\test\neg_test\',test_name));
I=double(image4)/255;
clu_kmeans=imkmeans(I,3);
clu_pic=clu_kmeans/3;
lbps = lbp(clu_pic);
data2(sz_pos(1)+n,:)=lbpst;
end
load data1
load data2
load svmStruct3
%数据降维
[COEFF SCORE latent]=princomp(data1(:,:));%训练集数据降维
pcaData1 = SCORE(:,1:k);
latent = 100*latent/sum(latent);
for i = 1:8
latent(i+1) = latent(i+1)+latent(i)
end
plot(latent(1:8));%画出前8个特征值所包含的图像信息比例
x0 = bsxfun(@minus,data2,mean(data2,1));
pcaData2_sw = x0*COEFF(:,:);
pcaData2 = pcaData2_sw(:,1:k);
%% 评估方法:交叉验证法
[train, test] = crossvalind('holdOut',label_train); %随机选择训练集合测试集
cp = classperf(label_train); %评估分类器性能
svmStruct3hog = svmtrain(pcaData1(train,1:k),label_train(train));%训练SVM分类器
%使用svmtrain进行训练,得到训练后的结构svmStruct3hog,在预测时使用
save svmStruct3hog %%保存 svmStruct3hog
cros = svmclassify(svmStruct3hog,pcaData1(test,1:k));
classperf(cp,cros ,test);
cp.CorrectRate
%% 测试
load svmStruct3hog
for i=1:sz_pos(1)
classes = svmclassify(svmStruct3,pcaData2(i,:));%classes的值即为分类结果
if classes==1
acc1=acc1+1;%记录正确分类的样本数
end
end
for j = sz_pos(1)+1:1383
classes = svmclassify(svmStruct3,pcaData2(j,:));%classes的值即为分类结果
if classes~=1
acc2=acc2+1;%记录正确分类的样本数
end
end
acc = acc1+acc2;
fprintf('精确度为:%5.2f%%\n',(acc/(sz_neg(1)+sz_pos(1)))*100);%计算预测的正确率%lbp特征提取代码
function result = lbp(varargin) % image,radius,neighbors,mapping,mode)
% Check number of input arguments.
error(nargchk(1,5,nargin));
image=varargin{1};
d_image=double(image);
if nargin==1
spoints=[-1 -1; -1 0; -1 1; 0 -1; -0 1; 1 -1; 1 0; 1 1];
neighbors=8;
mapping=0;
mode='h';
end
if (nargin == 2) && (length(varargin{2}) == 1)
error('Input arguments');
end
if (nargin > 2) && (length(varargin{2}) == 1)
radius=varargin{2};
neighbors=varargin{3};
spoints=zeros(neighbors,2);
% Angle step.
a = 2*pi/neighbors;
for i = 1:neighbors
spoints(i,1) = -radius*sin((i-1)*a);
spoints(i,2) = radius*cos((i-1)*a);
end
if(nargin >= 4)
mapping=varargin{4};
if(isstruct(mapping) && mapping.samples ~= neighbors)
error('Incompatible mapping');
end
else
mapping=0;
end
if(nargin >= 5)
mode=varargin{5};
else
mode='h';
end
end
if (nargin > 1) && (length(varargin{2}) > 1)
spoints=varargin{2};
neighbors=size(spoints,1);
if(nargin >= 3)
mapping=varargin{3};
if(isstruct(mapping) && mapping.samples ~= neighbors)
error('Incompatible mapping');
end
else
mapping=0;
end
if(nargin >= 4)
mode=varargin{4};
else
mode='h';
end
end
% Determine the dimensions of the input image.
[ysize xsize] = size(image);
miny=min(spoints(:,1));
maxy=max(spoints(:,1));
minx=min(spoints(:,2));
maxx=max(spoints(:,2));
% Block size, each LBP code is computed within a block of size bsizey*bsizex
bsizey=ceil(max(maxy,0))-floor(min(miny,0))+1;
bsizex=ceil(max(maxx,0))-floor(min(minx,0))+1;
% Coordinates of origin (0,0) in the block
origy=1-floor(min(miny,0));
origx=1-floor(min(minx,0));
% Minimum allowed size for the input image depends
% on the radius of the used LBP operator.
if(xsize < bsizex || ysize < bsizey)
error('Too small input image. Should be at least (2*radius+1) x (2*radius+1)');
end
% Calculate dx and dy;
dx = xsize - bsizex;
dy = ysize - bsizey;
% Fill the center pixel matrix C.
C = image(origy:origy+dy,origx:origx+dx);
d_C = double(C);
bins = 2^neighbors;
% Initialize the result matrix with zeros.
result=zeros(dy+1,dx+1);
%Compute the LBP code image
for i = 1:neighbors
y = spoints(i,1)+origy;
x = spoints(i,2)+origx;
% Calculate floors, ceils and rounds for the x and y.
fy = floor(y); cy = ceil(y); ry = round(y);
fx = floor(x); cx = ceil(x); rx = round(x);
% Check if interpolation is needed.
if (abs(x - rx) < 1e-6) && (abs(y - ry) < 1e-6)
% Interpolation is not needed, use original datatypes
N = image(ry:ry+dy,rx:rx+dx);
D = N >= C;
else
% Interpolation needed, use double type images
ty = y - fy;
tx = x - fx;
% Calculate the interpolation weights.
w1 = (1 - tx) * (1 - ty);
w2 = tx * (1 - ty);
w3 = (1 - tx) * ty ;
w4 = tx * ty ;
% Compute interpolated pixel values
N = w1*d_image(fy:fy+dy,fx:fx+dx) + w2*d_image(fy:fy+dy,cx:cx+dx) + ...
w3*d_image(cy:cy+dy,fx:fx+dx) + w4*d_image(cy:cy+dy,cx:cx+dx);
D = N >= d_C;
end
% Update the result matrix.
v = 2^(i-1);
result = result + v*D;
end
%Apply mapping if it is defined
if isstruct(mapping)
bins = mapping.num;
for i = 1:size(result,1)
for j = 1:size(result,2)
result(i,j) = mapping.table(result(i,j)+1);
end
end
end
if (strcmp(mode,'h') || strcmp(mode,'hist') || strcmp(mode,'nh'))
% Return with LBP histogram if mode equals 'hist'.
result=hist(result(:),0:(bins-1));
if (strcmp(mode,'nh'))
result=result/sum(result);
end
else
%Otherwise return a matrix of unsigned integers
if ((bins-1)<=intmax('uint8'))
result=uint8(result);
elseif ((bins-1)<=intmax('uint16'))
result=uint16(result);
else
result=uint32(result);
end
end
end%k-means图像聚类分割
function [F,C]=imkmeans(I,C)
% I:图像矩阵,支持彩色或者灰度图
% C:聚类中心,可以是整数或者数组,整数表示随机选择K个聚类中心
% F:样本聚类编号
if nargin~=2
error('IMKMEANS:InputParamterNotRight','只能有两个输入参数!');
end
if isempty(C)
K=2;
C=[];
elseif isscalar(C)
K=C;
C=[];
else
K=size(C,1);
end
%% I.提取像素点特征向量
X=exactvecotr(I);
%% II.搜索初始聚类中心
if isempty(C)
C=searchintial(X,'sample',K);
end
%% III.循环搜索聚类中心
Cprev=rand(size(C));
while true
%计算样本到中心的距离
D=sampledist(X,C,'euclidean');
%找出最近的聚类中心
[~,locs]=min(D,[],2);
%使用样本均值更新中心
for i=1:K
C(i,:)=mean(X(locs==i,:),1);
end
%判断聚类算法是否收敛
if norm(C(:)-Cprev(:))