逻辑回归--乳腺癌数据集
逻辑回归–乳腺癌数据集
一直以为西瓜书中没有逻辑回归这一内容,原来是放在了线性模型这一章节。里面称之为“对数几率回归”。原文给出的理由是:
有文献译为“逻辑回归”,但中文“逻辑”与logistic 和 logit 的含义相去甚远,因此本书意译为“对数几率回归”,简称”对率回归“。
实验要求
实验要求:
- 使用乳腺癌数据集作为实验数据集(load_breast_cancer),加载并划分数据集
- 使用sklearn的逻辑回归分类器进行模型训练,并进行至少3个参数调参
(sklearn的线性模型的API文档:https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model) - 使用多项式回归对sklearn的逻辑回归分类器进行优化。
- 编写一个逻辑回归分类器,使用多项式回归优化模型。
实验内容
首先导入相关的库
from sklearn import preprocessing
from sklearn.datasets import load_breast_cancer #加载数据集-乳腺癌数据集
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler # 标准化工具
import numpy as np
from math import exp
from sklearn.preprocessing import MinMaxScaler
1.使用乳腺癌数据集作为实验数据集(load_breast_cancer),加载并划分数据集
cancer = load_breast_cancer() # 加载数据集
print(cancer.keys())
# Out: dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])
X = cancer.data
Y = cancer.target
print('数据大小:',X.shape)
print('---其中有{0}条数据,有{1}个特征'.format(X.shape[0],X.shape[1]))
print('标签是:',Y.shape)
print('---其中有{0}条数据'.format(Y.shape[0]))
# Out: 数据大小: (569, 30)
# ---其中有569条数据,有30个特征
# 标签是: (569,)
# ---其中有569条数据
# 归一化处理
mm = MinMaxScaler()
X = mm.fit_transform(X)
# 划分数据集和训练集,其中测试集占0.3 random_state 是 随机数种子,0或不填每次会不一样
x_train,x_test,y_train,y_test = train_test_split(X,Y,test_size=0.3)
1.1归一化处理
这里使用的是 MinMaxScaler(),把X归一化到0-1这个区间,加速模型收敛。如果注释掉归一化处理,那正确率会明显下降。且自己编写的逻辑回归分类器也会出错,详见4.1
2.使用sklearn的逻辑回归分类器进行模型训练,并进行至少3个参数调参
lr = LogisticRegression(penalty='l2',max_iter=5000,tol=1e-2)
# penalty:惩罚项,默认为l2
# max_iter: 最大迭代次数
# tol:停止求解的标准,float类型,默认为1e-4。就是求解到多少的时候,停止,认为已经求出最优解
lr.fit(x_train,y_train)
lr.predict(x_test)
score = lr.score(x_test,y_test)
print("训练所得特征参数为:",lr.coef_)
print("所得截距:",lr.intercept_)
print("得分为:%.3f"%score)
2.1LogisticRegression参数解释
关于tol的解释:
当某一轮,所有参数的梯度更新量中最大的梯度更新量(前一次和后一次进行比较)都小于给定的阈值的时候,则认为模型已经收敛,此时模型训练自动停止。另外如果模型的收敛次数达到了max_iter的时候也会自动停止。
此外,如果模型的收敛次数达到了max_iter的时候,还没达到规定的tol值,此时会抛出一个错误,STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.此时,最好是把数据归一化,让数据相对集中,收敛速度加快;或者把迭代次数调高,再或者把tol调高些。
其他参数解释
3.使用多项式回归对sklearn的逻辑回归分类器进行优化
poly = PolynomialFeatures(degree=2)
print('训练集的维度:',x_train.shape)
x_train_poly = poly.fit_transform(x_train)
print('扩展后训练集的维度:',x_train_poly.shape)
lr = LogisticRegression(penalty='l2',max_iter=10000)# 逻辑回归
lr.fit(x_train_poly, y_train)
x_test_poly = poly.fit_transform(x_test) # 多测试集进行扩展,为了进行检测与分数预测
y_p = lr.predict(x_test_poly)
score = lr.score(x_test_poly,y_test)
print("分数为:%.3f"%score)
4.编写一个逻辑回归分类器,使用多项式回归优化模型。
自己编写的分类器
class LogisticReressionClassifier:
def __init__(self, max_iter=200, learning_rate=0.01):
self.max_iter = max_iter
self.learning_rate = learning_rate
def sigmoid(self, x):
return 1 / (1 + exp(-x))
# 在原本的X前面加上常数1,常数项
def data_matrix(self, X):
data_mat = []
for d in X:
data_mat.append([1.0, *d])
return data_mat
def fit(self, X, y):
data_mat = self.data_matrix(X) # 1.对X前置加一列1,方便接下来的矩阵计算。
self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32) # 2.初始化权重和偏移量。
for iter_ in range(self.max_iter): # 3.根据迭代次数进行迭代训练
for i in range(len(X)): # 4.这里训练集shape是(398,30),即len是398,特征量为30
result = self.sigmoid(np.dot(data_mat[i], self.weights)) # 5.得到此次预测值,需要通过sigmoid处理,得到正确的概率
error = y[i] - result # 得到错误的概率
# 这里使用的是梯度上升法
self.weights += self.learning_rate * error * np.transpose( # np.transpose是对矩阵进行转置
[data_mat[i]])
print('(学习率={},最大迭代次数={})'.format(self.learning_rate, self.max_iter))
def score(self, X_test, y_test):
right = 0
X_test = self.data_matrix(X_test)
for x, y in zip(X_test, y_test): # 使用zip打包
result = np.dot(x, self.weights)
if (result > 0 and y == 1) or (result < 0 and y == 0):
right += 1
return right / len(X_test)
zip的效果:
x = np.array([[1,2,3],[3,4,5],[6,7,8]])
y = np.array([[5],[6],[7]])
In: print(*zip(x,y))
Out:(array([1, 2, 3]), array([5])) (array([3, 4, 5]), array([6])) (array([6, 7, 8]), array([7]))
In: for a,b in zip(x,y):
print(a,b)
Out: [1 2 3] [5]
[3 4 5] [6]
[6 7 8] [7]
训练并打印分数
lr_clf = LogisticReressionClassifier()
lr_clf.fit(x_train, y_train)
score = lr_clf.score(x_test, y_test)
print("分数为:%.3f"%score)
–公式推论–
这里是一篇我自认为比较简单易懂的推论:公式推论
下面是结合西瓜书中的推导过程和个人理解的推导过程。
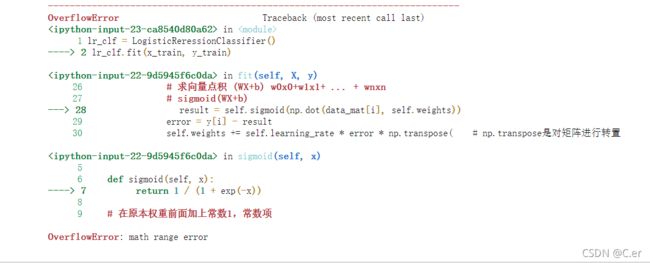
4.1 如果没有归一化处理时报错
看到报错内容为:math range error。
这是由于,在没有归一化之前,这些原始数据都非常的离散(这里的离散指没有相对集中),我们可以打印出错时的数字,如在sigmoid函数加一句print(x),得到最后出错时的x是[-10610.26234112],以-x作为指数,结果可想而知,数太大越界了。
多项式回归优化模型
和上面一样,就是换了个训练器。
poly = PolynomialFeatures(degree=2)
lr_clf.fit(x_train_poly, y_train)
x_test_poly = poly.fit_transform(x_test) # 多测试集进行扩展,为了进行检测与分数预测
score = lr_clf.score(x_test_poly,y_test)
print("分数为:%.3f"%score)