【图像处理】——Python实现图像特征提取&BP神经网络实现图像二分类

目录

 

一、图像特征提取

二、BP实现图像二分类

1、输入层、隐层、输出层结点个数设置

（1）one hot码（假设是n分类问题）

(2)一个输出，输出层结点为1

---

一、图像特征提取

图像具有灰度特征、GLCM特征、Huments不变矩特征、LBP特征，具体可参考我主页的其他博客

import cv2
import numpy as np
from numpy import histogram

#灰度特征
def GrayFea(faultness):
	'''
	:param faultness: 灰度图像
	:return: list->(4)
	'''
	hist0 = cv2.calcHist([faultness], [0], None, [256], [0, 255])
	h, w = faultness.shape
	hist = hist0 / (h * w)

	# 灰度平均值
	mean_gray = 0
	for i in range(len(hist)):
		mean_gray += i * hist[i]

	# 灰度方差
	var_gray = 0
	for i in range(len(hist)):
		var_gray += hist[i] * (i - mean_gray) ** 2

	# 能量
	##归一化
	max_ = np.max(hist)
	min_ = np.min(hist)
	hist_ = (hist - min_) / (max_ - min_)
	##求解能量
	energy = 0
	for i in range(len(hist_)):
		energy += hist_[i] ** 2

	#灰度对比度
	con = np.max(faultness)-np.min(faultness)
	gray_fea = [mean_gray[0], var_gray[0], energy[0],con]
	return gray_fea


#计算不变矩特征
def huMoments(faultness):
    '''
    opencv_python自带求矩以及不变矩的函数
    :param faultness: 灰度图像，对于二值图像来说就只有两个灰度0和255
    :return: 返回以10为底对数化后的hu不变矩，（7*1）
    '''
    moments = cv2.moments(faultness)#返回的是一个字典，三阶及以下的几何矩（mpq）、中心矩(mupq)和归一化的矩(nupq)
    humoments = cv2.HuMoments(moments)#根据几何矩（mpq）、中心矩(mupq)和归一化的矩(nupq)计算出hu不变矩
    # 因为直接计算出来的矩可能很小或者很大，因此取对数好比较,这里的对数底数为e,通过对数除法的性质将其转换为以10为底的对数
    humoment = (np.log(np.abs(humoments)))/np.log(10)
    humoment = -humoment.ravel()#将其变为一维的
    return humoment


#灰度共生矩阵GLCM
from skimage.feature import greycomatrix, greycoprops
import cv2

image = cv2.imread(r'E:bpPackage\colorful_lena.jpg',0)

def GLCM(grayImg):
	'''
	:param grayImg: 灰度图像
	:return: list->(24),因为GLCM特征有6个，每个特征取了四个方向的特征，因此共有24个特征值
	'''
	GLCMFeas = []
	#这一步类似于数据压缩，因为8位图像含有256个灰度级，这样会导致计算灰度共生矩阵是的计算量过大，因此将其进行压缩成16级，将灰度进行分区
	bins = np.array([0, 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 255]) #16-bit
	inds = np.digitize(grayImg, bins)#返回的是一个和image大小一样的矩阵，只是矩阵元素表示的是image中元素在bins中的区间位置，小于0为0,0-16为1，以此类推
	max_value = inds.max()+1
	matrix_coocurrence = greycomatrix(inds, #需要进行共生矩阵计算的numpy矩阵
									  [1],#步长
									  [0, np.pi/4, np.pi/2, 3*np.pi/4],#方向角度
									  levels=max_value, #共生矩阵阶数
									  normed=False, symmetric=False)
	print(matrix_coocurrence)
	#P[i,j,d,theta]返回的是一个四维矩阵，各维代表不同的意义


	# GLCM properties
	#对比度CON
	# [[2.26653266 3.03593344 1.1861809  2.33115325]]返回的是一个数组，要将其元素求出来，首先进行取0元素然后再进行extend加入列表中
	contrast = greycoprops(matrix_coocurrence,'contrast')
	GLCMFeas.extend(contrast[0])
	#差异性DISL
	dissimilarity = greycoprops(matrix_coocurrence,'dissimilarity')
	GLCMFeas.extend(dissimilarity[0])
	#反差分矩阵HOMO
	homogeneity = greycoprops(matrix_coocurrence,'homogeneity')
	GLCMFeas.extend(homogeneity[0])
	#熵ENT
	energy = greycoprops(matrix_coocurrence, 'energy')
	GLCMFeas.extend(energy[0])
	#相关性COR
	correlation = greycoprops(matrix_coocurrence, 'correlation')
	GLCMFeas.extend(correlation[0])
	#角二阶矩（能量）ASM
	asm = greycoprops(matrix_coocurrence, 'ASM')
	GLCMFeas.extend(asm[0])
	print(GLCMFeas)
	return GLCMFeas

#LBP特征
from skimage import feature as skft
def LBPFeas(grayimg):
	'''
	:param grayimg: 灰度图像
	:return: 返回list->(256)
	'''
	#uniform,nri_uniform,var
	lbp = skft.local_binary_pattern(grayimg,P=8,R=1,method='nri_uniform')#将原图分割成256个小子图像，得到每个小区域的LBP十进制直方图，然后将256个直方图进行叠加得到全局直方图
	lbp = lbp.astype(np.uint8)
	max_bins = int(lbp.max() + 1)  # 得到图片中最大的灰度级别
	# hist size:256
	#对图像的256个子图像的LBP值进行统计
	LBPHist,_ = np.histogram(lbp, bins=max_bins, range=(0, max_bins),density=False)  # 绘制每一个小区域的直方图
	return list(LBPHist.ravel())

#求得一个图像的所有特征
def CalAllFeas(img):
	'''
	:param img: 灰度图像
	:return: 返回一个含有所有特征的列表，4+7+24+256
	'''
	##存放全部特征
	Allfeas = []
	##加入灰度特征
	grayFeas = GrayFea(img)
	Allfeas.extend(grayFeas)
	##加入不变矩特征
	HuMomentFeas = huMoments(img)
	Allfeas.extend(HuMomentFeas)
	##加入共生矩阵特征
	GlcmFeas = GLCM(img)
	Allfeas.extend(GlcmFeas)
	##加入LBP纹理特征
	LbpFeas = LBPFeas(img)
	Allfeas.extend(LbpFeas)
	return Allfeas

#进行特征特取以及标签标记
def main():
	'''
	特征标记规则：渣点图像标记为1，其余标记为0
	:return: 返回含标记的数据集，第一位是图片编号，编号规则：渣点图像编号从1-102，非渣点从103-203
	'''
	dataSets = []#数据集
	PosImgDatasets = []#渣点图像数据集
	NegImgDatasets = []#非渣点图像数据集
	for i in range(1,103):
		img = cv2.imread(r'E:bpPackage\PositiveImg\ObjImg{}.jpg'.format(i),0)
		PosAllFeas = [i]#加入图片编号
		PosAllFeas.extend(CalAllFeas(img))
		PosAllFeas.append(1)
		PosImgDatasets.append(PosAllFeas)
	dataSets.extend(PosImgDatasets)

	for i in range(1,101):
		img = cv2.imread(r'E:bpPackage\NegativeImg\NoObjImg{}.jpg'.format(i),0)
		NegAllFeas = [i+len(dataSets)]
		NegAllFeas.extend(CalAllFeas(img))
		NegAllFeas.append(0)
		NegImgDatasets.append(NegAllFeas)
	dataSets.extend(NegImgDatasets)
	dataSets = np.array(dataSets)
	#将数组以元素为浮点数的形式写入TXT文件中，元素间用\t进行分割
	np.savetxt(r"E:dataSets94.txt", dataSets, fmt='%f', delimiter='\t')

if __name__ == '__main__':
	main()

二、BP实现图像二分类

1、输入层、隐层、输出层结点个数设置

参考：《BP神经网络的隐含层，输入层，输出层的节点数确定》

《神经网络隐藏层节点数最少可以是多少个？》

输入层结点个数等于一个样本的特征个数

隐层结点个数一般是输入层结点个数开根号取整+1

输出层结点取决于你分类的方式

（1）one hot码（假设是n分类问题）

        可以实现多分类的输出，对于一个样本来说，最终会得到n个输出值，输出值是样本归属于每一类的概率，我们最后将其归类到概率最大的那一类中，这种规则叫做通吃规则，这时候为了方便，我们将最大概率的值设置为1，其余的设置为0，这样对于每一个样本的分类都对应一个行向量，[0 0 0 0 ... 1 0 0 0 ... 0 0],这里1所对应的类别就是样本的类别，要是有m个样本，则得到的将会是nXm的一个分类矩阵

关于one hot在实例中如何实现的可以参考：Python 基于BP神经网络的鸢尾花分类

关键代码：

# 结果的维度
    n_rows = y_test.shape[0]
    n_cols = y_test.shape[1]

    # 预测值结果存储
    output = np.empty(shape=(n_rows, n_cols), dtype=int)

    for i in range(n_rows):
        for j in range(n_cols):
            if a2[i][j] > 0.5:
                output[i][j] = 1
            else:
                output[i][j] = 0

(2)一个输出，输出层结点为1

这个就是直接将输出的结果作为标签，以三分类为准，输出0为类别一，输出1为类别二，输出2为类别三

本案例就是通过这种方式进行分类的

import pandas as pd
import numpy as np
import datetime
from sklearn.utils import shuffle

#####################################BP神经网络模型创建#########################################
# 1.初始化参数
def initialize_parameters(n_x, n_h, n_y):#n_x = 94一个样本具有的特征个数,n_h = 10,n_y = 1
    np.random.seed(2)
    # 权重和偏置矩阵
    w1 = np.random.randn(n_h, n_x) * 0.01#(10,94)
    b1 = np.zeros(shape=(n_h, 1))#(10,1)
    w2 = np.random.randn(n_y, n_h) * 0.01#(1,10)
    b2 = np.zeros(shape=(n_y, 1))#(1,1)

    # 通过字典存储参数
    parameters = {'w1': w1, 'b1': b1, 'w2': w2, 'b2': b2}
    return parameters

# 2.前向传播
def forward_propagation(X, parameters):
    w1 = parameters['w1']#(10,94)
    b1 = parameters['b1']#(10,1)
    w2 = parameters['w2']#(1,10)
    b2 = parameters['b2']#(1,1)

    # 通过前向传播来计算a2,x(94,141)
    z1 = np.dot(w1, X) + b1    #(10,141) # 这个地方需注意矩阵加法：虽然(w1*X)和b1的维度不同，但可以相加
    a1 = 1 / (1 + np.exp(-z1)) #(10,141) # 使用tanh作为第一层的激活函数
    z2 = np.dot(w2,a1) + b2   #(1,141)
    a2 =  1 / (1 + np.exp(-z2)) #(1,141) 使用sigmoid作为第二层的激活函数

    # 通过字典存储参数
    cache = {'z1': z1, 'a1': a1, 'z2': z2, 'a2': a2}

    return a2, cache


# 3.计算代价函数
def compute_cost(a2, Y, parameters):
    '''
    :param a2: (1,141)最后一层经过激活函数处理的
    :param Y: (1,141)标签
    :param parameters: 
    :return: 
    '''
    m = Y.shape[1]      #Y(1,141) Y的列数即为总的样本数

    # 采用交叉熵（cross-entropy）作为代价函数
    logprobs = np.multiply(np.log(a2), Y) + np.multiply((1 - Y), np.log(1 - a2))
    cost = - np.sum(logprobs) / m

    return cost


# 4.反向传播（计算代价函数的导数）
def backward_propagation(parameters, cache, X, Y):
    m = Y.shape[1]

    w2 = parameters['w2']

    a1 = cache['a1']
    a2 = cache['a2']

    # 反向传播，计算dw1、db1、dw2、db2
    dz2 = a2 - Y
    dw2 = (1 / m) * np.dot(dz2, a1.T)
    db2 = (1 / m) * np.sum(dz2, axis=1, keepdims=True)
    dz1 = np.multiply(np.dot(w2.T, dz2), 1 - np.power(a1, 2))
    dw1 = (1 / m) * np.dot(dz1, X.T)
    db1 = (1 / m) * np.sum(dz1, axis=1, keepdims=True)

    grads = {'dw1': dw1, 'db1': db1, 'dw2': dw2, 'db2': db2}

    return grads


# 5.更新参数
def update_parameters(parameters, grads, learning_rate=0.0075):
    w1 = parameters['w1']
    b1 = parameters['b1']
    w2 = parameters['w2']
    b2 = parameters['b2']

    dw1 = grads['dw1']
    db1 = grads['db1']
    dw2 = grads['dw2']
    db2 = grads['db2']

    # 更新参数
    w1 = w1 - dw1 * learning_rate
    b1 = b1 - db1 * learning_rate
    w2 = w2 - dw2 * learning_rate
    b2 = b2 - db2 * learning_rate

    parameters = {'w1': w1, 'b1': b1, 'w2': w2, 'b2': b2}

    return parameters


# 建立神经网络
def nn_model(X, Y, n_h, n_input, n_output, num_iterations=100000, print_cost=False):
    np.random.seed(3)
    n_x = n_input           # 输入层节点数
    n_y = n_output          # 输出层节点数

    # 1.初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)

    # 梯度下降循环
    for i in range(0, num_iterations):
        # 2.前向传播
        a2, cache = forward_propagation(X, parameters)
        # 3.计算代价函数
        cost = compute_cost(a2, Y, parameters)
        # 4.反向传播
        grads = backward_propagation(parameters, cache, X, Y)
        # 5.更新参数
        parameters = update_parameters(parameters, grads)

        # 每1000次迭代，输出一次代价函数
        if print_cost and i % 1000 == 0:
            print('迭代第%i次，代价函数为：%f' % (i, cost))

    return parameters

# 对模型进行测试
def predict(parameters, x_test, y_test):
    '''
    :param parameters: 神经网络参数，权重和偏置
    :param x_test: 用于测试的样本集
    :param y_test: 用于测试的样本集对应的真实标签分类
    :return: 返回的是对测试数据集预测的标签output以及预测的正确率acc
    '''
    w1 = parameters['w1']
    b1 = parameters['b1']
    w2 = parameters['w2']
    b2 = parameters['b2']

    z1 = np.dot(w1, x_test) + b1
    a1 = 1 / (1 + np.exp(-z1))
    z2 = np.dot(w2, a1) + b2
    a2 = 1 / (1 + np.exp(-z2))
    # 结果的维度
    n_rows = y_test.shape[0]#1
    n_cols = y_test.shape[1]#61

    # 预测值结果存储
    output = np.empty(shape=(n_rows, n_cols), dtype=int)

    # 取出每条测试数据的预测结果,大于0.5的设置为1，小于0.5的设置为0
    for i in range(n_cols):
        for j in range(n_rows):
            if a2[j,i] > 0.5:
                output[j][i] = 1
            else:
                output[j][i] = 0

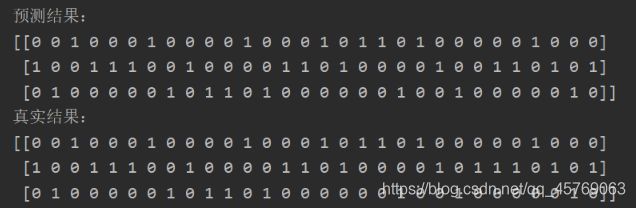
    # print('预测结果：')
    # print(output)
    # print('真实结果：')
    # print(y_test)

    count = 0
    for k in range(0, n_cols):
        if output[0][k] == y_test[0][k]:
            count = count + 1
    acc = count / int(y_test.shape[1]) * 100
    # print('准确率：%.2f%%' % acc)
    return output,acc


#数据集处理
def createdataset(path):
    '''
    :param path: TXT文件路径
    :return: 返回的是数据集->list
    '''
    #通过utf-8格式打开含有中文的TXT文件
    datasets = open(path,encoding='utf-8')
    #按行读取文件，得到的是一个列表，每一个元素是将一行作为一个字符串
    lines = datasets.readlines()
    #遍历列表
    dataSets = []
    for line in lines:
        #通过去除首位空格和根据逗号来分割字符串，将一串字符串分割成了多个字符组成的列表
        line = line.strip().split('\t')
        line = list(map(float,line))#将字符串数字转化为浮点型数据
        dataSets.append(line)#将之前的数据集规整化为一个列表
    return dataSets

#划分数据集
def splitDatasets(dataSets,trainingSize):
    '''
    :param dataSets: 数据集，第一列是编号，最后一列是类别
    :param trainingSize: 训练集样本占比，小数表示一般为0.7
    :return: 返回训练集和测试集trainDatas(141,94),trainLabels(141,1),testDatas(61,94),testLabels(61,1)
    '''
    numOfData = len(dataSets)
    numOfTrainData = int(numOfData*trainingSize)
    trainSets = []
    testSets = []
    trainSets.extend(dataSets[0:numOfTrainData])
    testSets.extend(dataSets[numOfTrainData:])
    #划分数据集,将数据集进行转置,数据集通过转置来实现，标签集通过reshape来实现
    trainDatas = (np.array(trainSets)[:,1:-1]).T
    testDatas = (np.array(testSets)[:,1:-1]).T
    trainLabels = (np.array(trainSets)[:,-1]).reshape(1,numOfTrainData)
    testLabels = (np.array(testSets)[:,-1]).reshape(1,numOfData-numOfTrainData)
    return trainDatas,trainLabels,testDatas,testLabels

if __name__ == "__main__":
    # 读取数据
    start_time1 = datetime.datetime.now()
    path = r'E:bpPackage\dataSets94.txt'
    accSum = 0.0
    for i in range(10):
        print("------------------------第%d次------------------------------------"%i)
        dataSets = createdataset(path)#102个正样本，100个负样本
        dataSets = shuffle(dataSets)            # 打乱数据，这样保证了数据的随机性
        #划分数据集,训练样本特征、训练样本标签、测试样本特征、测试样本标签
        trainDatas, trainLabels, testDatas, testLabels = splitDatasets(dataSets,trainingSize=0.7)
        # print(trainDatas)
        # print(testDatas.shape)
        # 开始训练
        start_time = datetime.datetime.now()
        # 输入94个节点，隐层6个节点，输出1个节点，迭代100000次
        parameters = nn_model(trainDatas, trainLabels, n_h=10, n_input=94, n_output=1, num_iterations=100000, print_cost=True)
        end_time1 = datetime.datetime.now()
        print("训练模型用时：" + str((end_time1 - start_time).seconds) + 's' + str(round((end_time1 - start_time).microseconds / 1000)) + 'ms')
        # 对模型进行测试，随机测试100次，取正确率的平均值
        output,acc = predict(parameters, testDatas, testLabels)
        accSum += acc
    accMean = accSum/10
    print("正确率：",accMean)
    end_time2 = datetime.datetime.now()
    print("总用时：" + str((end_time2 - start_time1).seconds) + 's' + str(round((end_time2 - start_time).microseconds / 1000)) + 'ms')

上述可以调的超参数是：迭代次数：num_iterration,循环次数：10