1.ADT 抽象数据类型
抽象数据类型就是只定义一些操作,而不去具体实现这些操作,例如双端队列(Deque):
Deque ADT:
addFirst(Item x);
addLast(Item x);
boolean isEmpty();
int size();
printDeque();
Item removeFirst();
Item removeLast();
Item get(int index);在Project 1中,Deque只给了一些API,而具体的实现代码交由我们处理,由此产生了ArrayDeque和LinkedListDeque。
还有就是之前课上讲的List61B接口,只声明一些方法,具体实现为AList和SLList
准确来说,Java的interface并不是ADT,因为interface允许存在一些default的方法。
一个有趣的问题
现有一种抽象数据类型名为GrabBag,支持以下操作:
- insert(int x)向GrabBag中插入x
- int remove():随机地从GrabBag中移除
- int sample():随机地从GrabBag中返回一个样本值
- in size():返回GrabBag的元素个数
那么选取何种底层数据结构来实现GrabBag性能更佳?(数组 or 单链表)
答案是:数组
GrabBag中最需要考虑的操作就是随机地从Grab中删除一个元素,在数组中的实现为:
\(把数组最后一个元素B与待删除的元素A进行交换,然后指向数组末尾的指针减一\)
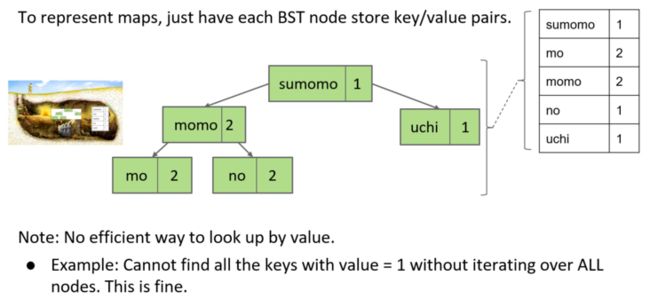
Map Example
几乎java.util library中最重要的interface是Collections,List,Set,Map均继承了该接口: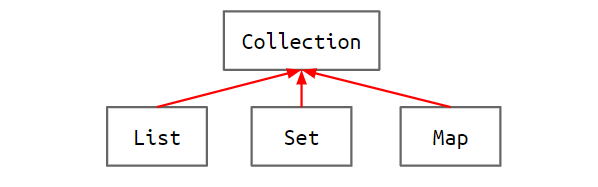
Map即
Map m = new TreeMap<>();
String[] text = {"sumomo", "mo", "momo", "mo",
"momo", "no", "uchi"};
for (String s : text) {
int currentCount = m.getOrDefault(s, 0);
m.put(s, currentCount + 1);
}
其中,getOrDefault(Object key, V defaultValue)方法获取指定 key 对应对 value,如果找不到 key ,则返回设置的默认值。
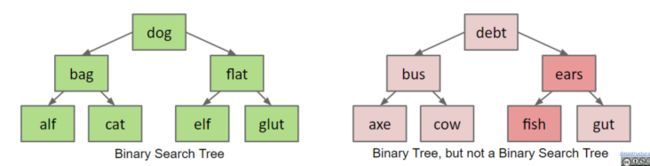
2.BST的定义
BST(Binary Search Tree)二叉搜索树的定义:
二叉搜索树是一棵有根树,且满足BST性质:
树的所有左子树的结点的值(key)小于根结点,且所有右子树的结点的值(key)大于根节点
BST的有序性必须满足:完整性,传递性和反对称性
给定两个key p和q:
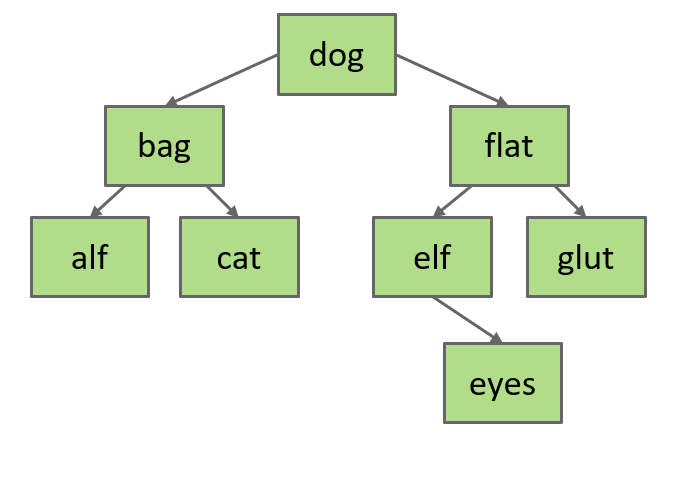
\( 反对称:p 且二叉搜索树中不能有重复的值,即不能出现相同的值(Josh的说法) 在二叉搜索树中查询某个值: 查询的路线即基于树的BST性质,对于经过的每个结点,将查询值与结点值进行比较, 在二叉搜索树中插入某个值: 如果没找到 例如下图二叉搜索树字母按字典排列,现在要向其中插入eyes: 大于dog-->进入右子树-->小于flat-->进入左子树-->大于elf-->作为其右孩子 三种情况: 情况1: 情况2: 情况3: 因此在g和m中二选一,将其作为新的根节点,替换掉k即可,假设我们选择g,需要做的是: 以上删除结点的方法被称作Hibbard deletion\( 传递:若p
3.BST的搜索
若小于当前结点值,则进入左子树继续搜索
若大于当前结点值,则进入右子树进行搜索,此后递归进行。
伪代码:static BST find(BST T, Key sk) {
if (T == null)
return null;
if (sk.equals(T.key))
return T;
else if (sk ≺ T.key)
return find(T.left, sk);
else
return find(T.right, sk);
}
时间复杂度

对于一棵bushy BST(稠密的二叉搜索树),当结点个数N为2的整次幂时,由于树的高度为\(log_{2}N\),其查询的时间复杂度为\( \Theta(logN) \)
4.BST的插入

static BST insert(BST T, Key ik) {
if (T == null)
return new BST(ik);
if (ik ≺ T.key)
T.left = insert(T.left, ik);
else if (ik ≻ T.key)
T.right = insert(T.right, ik);
return T;
}
5.BST的删除
直接将其删除,随后被垃圾回收器回收
假设我们要删除flat,删除之后一定要保持BST的性质,那么将flat的父节点dog指向flat的子树elf即可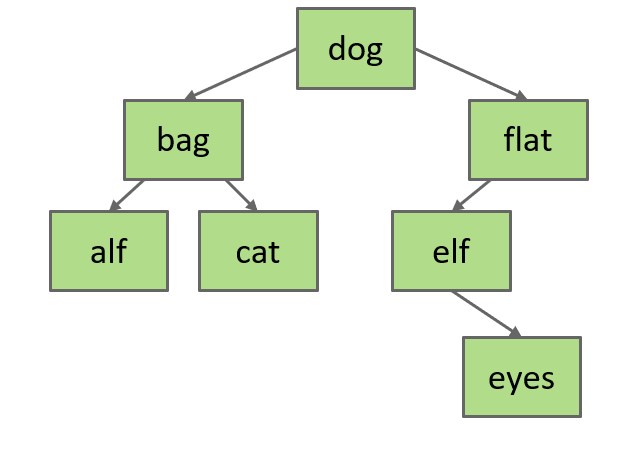
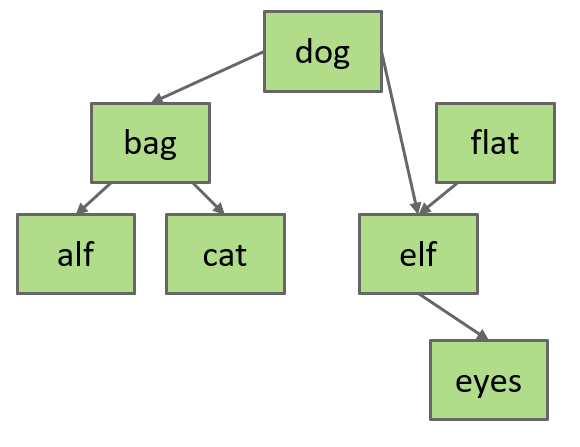

删除k
如果对二叉搜索树进行中序遍历,那么得到的结果就是一系列有序的字符,如图即abdefgkmprvxyz
假如我们称中序顺序中某一结点的前一个结点为前驱,后一个结点为后继,那么就是相当于用前驱或后继替换该结点的过程
由于本次课并没有讲中序遍历,以Josh的定义:
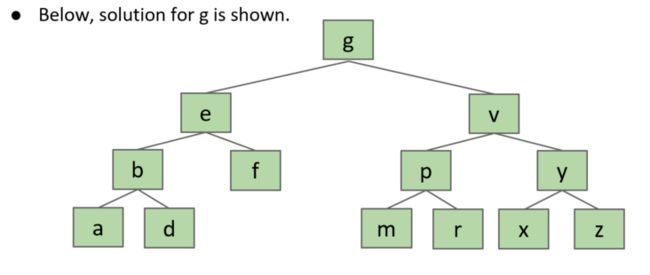
有人可能有疑问,假设前驱或后继有两个孩子,那么删除操作会变得更加复杂?
事实上,前驱或后继只有一个孩子或没有孩子,例如:
6.TreeMap的例子