今天再讲一篇关于利用贪心算法解决的题目。
一、金条切割问题
1、题目描述
一块金条切成两半,是需要花费和长度数值一样的铜板的。比如长度为20的金条,不管怎么切,都要花费20个铜板。一群人想整分整块金条,怎么分最省铜板?输入一个数组,返回分割的最小代价。
例如:
给定数组{10,20,30},代表一共三个人, 整块金条长度为10 + 20 + 30 = 60,金条要分成10, 20, 30三个部分(不考虑顺序)。
如果先把长度60的金条分成10和50,花费60;再把长度50的金条分成20和30,花费50;一共花费110铜板。
但如果先把长度60的金条分成30和30,花费60;再把长度30金条分成10和20,花费30;一共花费90铜板。
2、思路
(1)准备一个小根堆。将数组放到这个小根堆里。
(2)每次弹出堆顶的两个数求和为A,将A再放回小根堆里。
(3)一直执行第2步,直到堆只剩一个数。最后,每一次第二步A的累加和即是最后的结果。
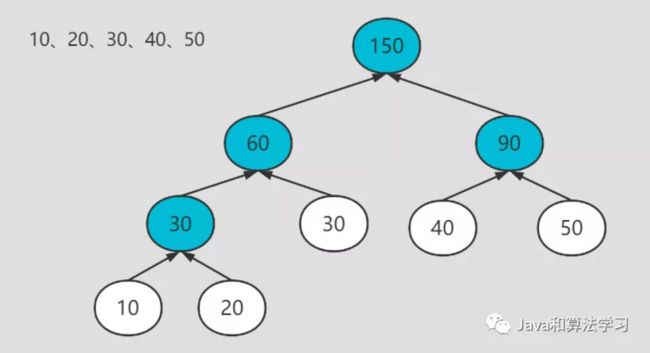
例如给定的金条长度为150,要分成10、20、30、40、50的块,最后花费的铜板数量即是上图中蓝色圆圈的和,即150+60+90+30=330。
也就是我们代码求解的时候是从叶子往根求的,求完后再从根往叶子即是金条的切割顺序,最后所有的叶子即是需要切成的块的大小。
3、代码
/**
* @author Java和算法学习:周一
*/
public static int lessMoneySplitGold(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
// 准备一个小根堆
Queue queue = new PriorityQueue<>();
// 将所有数放到小根堆中
for (Integer s : arr) {
queue.offer(s);
}
int result = 0;
int current;
while (queue.size() > 1) {
// 每次弹出堆顶两个数求和
current = queue.poll() + queue.poll();
result += current;
queue.offer(current);
}
return result;
}
二、点灯问题
1、题目描述
给定一个字符串str,只由 'X' 和 '.' 两种字符构成。'X’ 表示墙,不能放灯,点亮不点亮都可;'.' 表示居民点,可以放灯,需要点亮。如果灯放在i位置,可以让 i-1,i 和 i+1 三个位置被点亮。返回如果点亮str中所有需要点亮的位置,至少需要几盏灯。
2、思路
(1)i 位置是 'X’,不管,来到 i + 1位置
(2)i 位置是 '.' ,i + 1是 'X’,i 位置需要放灯,来到 i + 2位置
(3)i 位置是 '.' ,i + 1是 '.',i + 2是 '.',i + 1 位置需要放灯,来到 i + 3位置(此步即是贪心)
(4)i 位置是 '.' ,i + 1是 '.',i + 2是 'X’,i 或 i + 1 位置需要放灯,来到 i + 3位置
3、代码
/**
* @author Java和算法学习:周一
*/
public static int light(String light) {
char[] lightChars = light.toCharArray();
// 已经点灯的数量
int result = 0;
// 当前来到的位置
int i = 0;
while (i < lightChars.length) {
// i 位置是 'X’,不管,来到 i + 1位置
if (lightChars[i] == 'X') {
i++;
} else {
// i 位置是 '.' ,不管后续是怎样的,都要点一个灯
result++;
if (i + 1 == lightChars.length) {
break;
} else {
// i 位置是 '.' ,i + 1是 'X’,i 位置需要放灯,来到 i + 2位置
if (lightChars[i + 1] == 'X') {
i = i + 2;
} else {
// i 位置是 '.' ,i + 1是 '.',i + 2是 '.',i + 1 位置需要放灯,来到 i + 3位置
// i 位置是 '.' ,i + 1是 '.',i + 2是 'X’,i 或 i + 1 位置需要放灯,来到 i + 3位置
i = i + 3;
}
}
}
}
return result;
}
包含对数器的所有代码地址:https://github.com/monday-pro/algorithm-study/blob/master/src/basic/greedy/Light.java
三、IPO问题
1、题目描述
链接:https://leetcode-cn.com/probl...
假设 力扣(LeetCode)即将开始 IPO 。为了以更高的价格将股票卖给风险投资公司,力扣希望在 IPO 之前开展一些项目以增加其资本。由于资源有限,它只能在 IPO 之前完成最多 k 个不同的项目(串行做项目)。帮助力扣设计完成最多 k 个不同项目后得到最大总资本的方式。
给你 n 个项目。对于每个项目 i ,它都有一个纯利润 profits[i] ,和启动该项目需要的最小资本 capital[i] 。
最初,你的资本为 w 。当你完成一个项目时,你将获得纯利润,且利润将被添加到你的总资本中。
总而言之,从给定项目中选择 最多 k 个不同项目的列表,以最大化最终资本 ,并输出最终可获得的最多资本。
示例:
输入:k = 2, w = 0, profits = [1,2,3], capital = [0,1,1]
输出:4
解释:
由于你的初始资本为 0,你仅可以从 0 号项目开始。
在完成后,你将获得 1 的利润,你的总资本将变为 1。
此时你可以选择开始 1 号或 2 号项目。
由于你最多可以选择两个项目,所以你需要完成 2 号项目以获得最大的资本。
因此,输出最后最大化的资本,为 0 + 1 + 3 = 4。
2、思路
(1)准备一个小根堆,以启动项目需要的资本为标准,将所有项目放到小根堆里
(2)准备一个大根堆,把此时能做的项目从小根堆弹出来(拥有的资本 >= 项目启动资本),以利润为标准将项目放到大根堆中,弹出大根堆中的堆顶项目A,k加1,w加A的利润
(3)一直执行第2步,直到达到k个项目,最后返回w。
和游戏中的打怪升级很像,每次都在自己打得过的怪中找到收益最大的,一直打,自己越来越强同时保证不会被打败。
3、代码
/**
* @author Java和算法学习:周一
*/
public static int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
// 准备一个小根堆
Queue capitalSmallQueue = new PriorityQueue<>((a, b) -> a.capital - b.capital);
// 以启动项目需要的资本为标准,将所有项目放到小根堆中
for (int i = 0; i < profits.length; i++) {
capitalSmallQueue.offer(new Program(profits[i], capital[i]));
}
// 准备一个大根堆
// 放入的项目按项目的利润为标准
Queue profitsBigQueue = new PriorityQueue<>((a, b) -> b.profit - a.profit);
for (int i = 0; i < k; i++) {
// 当前拥有的资本 >= 项目的启动资本,将项目从小根堆中弹出放到大根堆中
while (!capitalSmallQueue.isEmpty() && w >= capitalSmallQueue.peek().capital) {
profitsBigQueue.offer(capitalSmallQueue.poll());
}
// 可能资本不足,造成现在还能做项目但是大根堆没有项目给你做了
if (profitsBigQueue.isEmpty()) {
return w;
}
w += profitsBigQueue.poll().profit;
}
return w;
}
public static class Program {
public int profit;
public int capital;
public Program(int profit, int capital) {
this.profit = profit;
this.capital = capital;
}
}
本题可以直接在LeetCode上测试,所以就不需要对数器来验证了。
4、测试结果
是不是发现贪心算法的解法正如上一篇所说,难的在于贪心策略的提出和证明,代码往往都比较简单,同时在面试时区分度也不是很高。