机器学习|R语言|利用随机森林对二手车交易价格进行评估
目录
利用随机森林对二手车交易价格进行评估
随机森林原理
前情提要
数据来源
数据预处理
数据补全与变量删除
数据异常值处理
随机森林模型建立与优化
树的棵树选取
自变量的选取
mtry参数的调整
maxdepth调参
扩展篇
GridSearch方法
交叉验证
利用随机森林对二手车交易价格进行评估
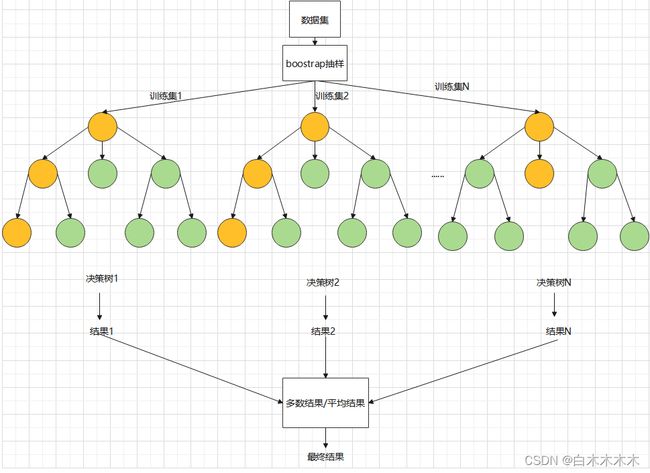
随机森林原理
随机森林算法作为一种取代神经网络等传统机器学习方法的分类回归算法,具有高准确率、不易过度拟合、对噪声及异常值容忍度高等特点。相比于 传统的多元线性回归模型,随机森林算法能够克服协变量之间复杂的交互作用。[1]随机森林算法通过构建多棵决策树形成森林,使用bootstrap重采样方法。实际操作为从原始样本中抽取一定数量样本,允许重复抽样;根据抽出的样本计算给定的统计量;重复上述步骤多次,得到多个计算的统计量结果;由统计量结果得到统计量方差。
随机森林算法流程为:
1、假设原始样本含量为N,应用bootstrap有放回随机抽取b个自助样本集(一般样本集中样本量越大回归效果越好),并由此构建b颗回归树,同时未抽取到的数据即袋外数据(OOB)作为随机森林的测试样本;
2、设原始数据变量个数为p,在每一个回归树的每个节点处随机抽取个变量( )作为备选分枝变量,一般取=p/3,然后再其中根据分枝优度准则选取最优分枝(同回归树模型建立);其中分枝优度准则是基于离均差平方和。
假设有p个自变量和连续型因变量Y。为预测二手车价格,将附件一数据处理后的各变量作为自变量X,将二手车交易价格作为连续型因变量Y。
对于树的某一节点t的样本为{..xn,yn},改节点样本量为N(t),由此可知该节点的的离均差平方和。假定该阶段t内所有可能的分枝集合(含变量和相应的切点)为A,分枝s将节点t分裂为两个子节点与,其中最佳分枝既为使得t节点的离均差平方和与分裂后的两个子节点对应的离均差平方和之和差距最大的分枝,即分裂后效果优于分裂前,使得各子节点内的变异最小。
3、每棵树开始自顶向下递归分枝,设定叶节点最小尺寸为5,并以此作为回归树生长的终止条件,即当叶节点数目小于5时,停止分枝;
4、将生成的b颗回归树组成随机森林回归模型。回归的效果评价采用带袋外数据(OOB)均方误差MSE,平均绝对误差MAE及拟合优度 。其中
在本模型中,选择划分训练集和测试级的比例为7:3。
前情提要
伴随我国经济的发展,汽车市场日渐繁荣,在新车保有量逐年攀升的同时,也有更多的消费者从观念上接受了二手车。2021年国内的二手车交易量为1758.51万辆,同比2020年1434.14万辆增长了22.6%。二手车交易量的增加带来了更大的二手车交易市场,同时也对二手车价值评估提出了更高的要求。
如今大数据、机器学习、深度学习等概念与技术已日渐普及,且逐渐开始落地,帮助企业降低实际的运作与生产中的成本。在一些汽车行业发达的国家(美、日、德等),利用大数据技术进行二手车交易价格的评估已在大企业中得到了广泛应用,而在中国大数据技术还未普及。本篇文章便基于随机森林建立预测模型对二手车交易价格进行评估。
数据来源
本文所采用数据来自《2021年MathorCup高校数学建模挑战赛——大数据竞赛》中赛道A所附带数据集,共两个附件(附件1:估价训练集与附件2:估价验证集)。训练集共有36列30000行,其中包含了车系、厂商类型、展销时间、新车价等20列车辆本身信息与市场信息。除此之外还包含了15列匿名数据,匿名数据即未给出数据具体含义。最后一列为二手车的准确交易价格。验证集与训练集数据类型相同,共10000行数据。我们此篇文章仅采用附件1:训练集中的数据。
导入包及数据读取:
###导入所需包
library(datasets)
library(plyr)
library(randomForest)
library(xlsx)
require(caret)
library(ggplot2)
library(vioplot)
library(dplyr)
library(tidyverse)
###数据的读取
set.seed(987654321) #设置随机种子
data <- read.csv('F:/R/处理数据.csv')
data <- data[,c(-1,-2)] #由于数据集的前两列为数据表自带序号与车辆id,属于无用信息,故删除
数据预处理
数据补全与变量删除
首先,对附件1和附件2中训练集和验证集进行数据预处理。附件一和附件二的数据处理方法相同。分析各数据中存在的缺失值数量。统计出的缺失数量如下:
| 缺失变量名称 |
附件1:估价训练数据 |
| country |
3757 |
| maketype |
3641 |
| modelyear |
312 |
| carCode |
9 |
| gearbox |
1 |
| anonymousFeature1 |
1582 |
| anonymousFeature4 |
12108 |
| anonymousFeature7 |
18044 |
| anonymousFeature8 |
3775 |
| anonymousFeature9 |
3744 |
| anonymousFeature10 |
6241 |
| anonymousFeature11 |
461 |
| anonymousFeature12 |
0 |
| anonymousFeature13 |
1619 |
| anonymousFeature15 |
27580 |
针对变量缺失个数结合分析,有下表中处理方法:
| 变量 |
处理方式 |
| country |
众数补全 |
| maketype |
|
| modelyear |
|
| carcode |
|
| anonymousFeature8 |
|
| anonymousFeature9 |
|
| anonymousFeature10 |
|
| anonymousFeature1 |
删除变量 |
| anonymousFeature4 |
|
| anonymousFeature7 |
|
| anonymousFeature15 |
|
| anonymousFeature13 |
|
| tradeTime |
计算差值构造新变量 |
| licenseDate |
|
| anonymousFeature12 |
拆分成三变量后对缺失值进行众数补全 |
| anonymousFeature11 |
特殊值代替 |
其中country为国别,maketype为厂商类型,modelyear为年款,carcode为国标码,gearbox为变速箱,均可看做分类型数据,使用其对应数据的众数补全。需要注意,由于附件2中数据量远远小于附件1,因此附件2验证集的缺失数据均用附件1对应数据的众数进行补全,从而确保更加合理。
匿名变量8,匿名变量9,匿名变量10只存在几种可能的数值,同样可看做分类型数据,采用众数补全。分析原数据发现,匿名变量1的数据值全为1,方差为0,无信息量,因此剔除。匿名变量4,匿名变量7,匿名变量15包含大量缺失值,仅有少部分有效值,因此剔除。匿名13和上牌日期与注册日期相近,为避免数据重复使用,增加工作量,因此剔除匿名13和上牌日期。
考虑二手车的使用时间对二手车价格影响较大,因此用展销日期减去上牌日期构造新变量:二手车使用天数。由于展销日期年份相同,方差为0,因此剔除。此外,保留注册日期的年份,而将影响较小的月份,日期数据剔除。
匿名变量11有1, 1+2,3+2,(1+2,4+2),等多种类型,亦可看做分类型数据,分别用数值1,2,3,4代表这四种类型,并取众数进行补全。匿名变量12为三个乘数相乘的形式,猜测为长宽高,相乘以表示车的体积等物理量,因此将三个乘数分为三列数据,形成三个新变量,以增强数据的完整性,最终形成项目所采用的数据集。
数据预处理脚本代码(python):
import pandas as pd
from pandas import read_csv
# 列名
names = ['carid', 'tradeTime', 'brand', 'serial', 'model', 'mileage', 'color', 'cityId', 'carCode', 'transferCount',
'seatings',
'registerDate', 'licenseDate', 'country', 'maketype', 'modelyear', 'displacement', 'gearbox', 'oiltype',
'newprice']
# 填补众数列名
modenames = ['country', 'maketype', 'modelyear', 'carCode', 'gearbox', 'anonymousFeature1'
, 'anonymousFeature8', 'anonymousFeature9', 'anonymousFeature10']
# 删除列名
delete_name = ['anonymousFeature4', 'anonymousFeature7', 'anonymousFeature15', 'tradeTime'
, 'registerDate', 'licenseDate', 'anonymousFeature12', 'anonymousFeature13', 'anonymousFeature1']
# 记录对应众数
modedict = {}
# 填充众数
def fillmode(train, name):
mod = train[name].mode()
mod = mod.tolist()[0]
train[name].fillna(mod, inplace=True)
x = {name: mod}
modedict.update(x)
# 分割数据处理
def sepdata(train):
# # 时间处理
train['tradeTime'] = pd.to_datetime(train['tradeTime'])
train['registerDate'] = pd.to_datetime(train['registerDate'])
train['licenseDate'] = pd.to_datetime(train['licenseDate'])
train['registerDate_year'] = train['registerDate'].dt.year
train['used_time'] = train['tradeTime'] - train['licenseDate']
train['used_time'] = train['used_time'].dt.days
# 分割处理
res = train['anonymousFeature12'].str.split('*', expand=True)
train['length'] = res[0]
train['width'] = res[1]
train['high'] = res[2]
# 分割处理
train['anonymousFeature11'] = train['anonymousFeature11'].map(func)
# 匿名变量映射
def func(x):
if x == '1':
x = 1
elif x == '1+2':
x = 2
elif x == '3+2':
x = 3
else:
x = 4
return x
# 处理过程
def process(train, filename):
sepdata(train)
for name in names:
if name in modenames:
fillmode(train, name)
if name in delete_name:
train = train.drop(name, 1)
print(train)
# 加入长宽高众数
modedict.update({'length': train['length'].mode().tolist()[0]})
modedict.update({'width': train['width'].mode().tolist()[0]})
modedict.update({'high': train['high'].mode().tolist()[0]})
train.to_csv(filename)
# 处理验证数据
def process_eval(eval, filename):
sepdata(eval)
for name in names:
# 填补附件一众数
if name in modedict.keys():
eval[name].fillna(modedict[name], inplace=True)
if name in delete_name or name == 'price':
eval = eval.drop(name, 1)
eval['width'].fillna(modedict['width'], inplace=True)
eval['high'].fillna(modedict['width'], inplace=True)
eval['length'].fillna(modedict['width'], inplace=True)
print(eval)
eval.to_csv(filename)
if __name__ == "__main__":
for i in range(15):
names.append('anonymousFeature' + str(i + 1))
names.append('price')
train = read_csv('附件/附件1:估价训练数据.csv', sep='\t', names=names)
process(train, './附件/处理数据1.csv')
eval = read_csv('附件/附件2:估价验证数据.csv', sep='\t', names=names)
process_eval(eval, './附件/验证数据.csv')
数据异常值处理
在对数据进行初步处理之后,需要对给出的数据中存在明显错误的点进行异常处理。在本文中主要采用箱型图法对异常数据进行处理。箱型图是用来表示数据分散情况的统计图,主要反映了数据的分布特征。
在箱型图中主要具有五个点,分别称位上限,下限,Q3(上四分位数,即位置的数),Q2(中位数),Q1(下四分位数,即位置的数)。上限等于Q3+1.5IQR,下限等于Q1-1.5IQR,有IQR=Q3-Q1。当数据的超过其对应的箱型图的上限以及下限时,可以判断其为异常值。示意图如下:
去除异常值:
OutVals = boxplot(data[,'price'], plot=FALSE)$out
data <- data[-(which(data[,'price'] %in% OutVals)),] #去除price值异常的数据行
data <- data[-(which(data[,'country']==0)),] #有些country值为0,属于异常值范畴
我们将异常值去除,并在去除异常值前后分别建立随机森林模型比较性能。(除异常值所在行外其它数据均相同,随机森林所有参数采用默认参数)得到结果如下表:
| 异常值去除前 | 异常值去除后 | |
| R方 | 0.000266 | 0.934676 |
由此可见去除异常点后模型性能有极大提升,所以这一步相当关键。
随机森林模型建立与优化
树的棵树选取
此次项目我们对随机森林的ntree,mtry,maxdepth等三个重要参数进行调节,我们首先对ntree即随机森林中决策树的数量进行调节。
我们采用预处理后的数据,随机森林的参数设为默认:
train_sub <- sample(datasize,round(0.7*datasize)) #将数据集打乱
train_data <- data[train_sub,]
test_data <- data[-train_sub,] #按照7:3的比例将原始数据集随机划分为训练集与验证集
fit.rf1 <- randomForest(price~. ,data=train_data,importance=T) #生成随机森林预测模型
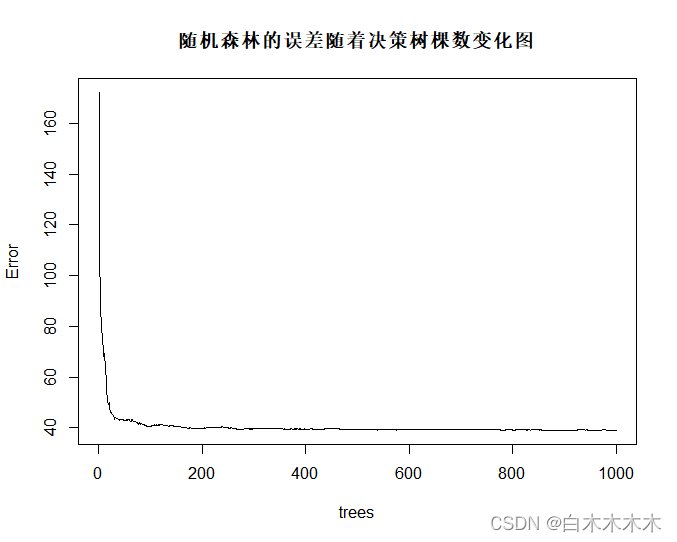
plot(fit.rf1) #采用plot()函数将随机森林的预测误差随着决策树棵数变化的曲线画出来
得到图:
由图可以看出当随机森林中决策树的棵树超过500后,随机森林的误差基本不变,为了使模型更高效,训练模型时间更短,我们将决策树的棵树确定为500。
自变量的选取
在建立初步的随机森林模型之后(采用默认参数),还需要对自变量个数进行相应的调整,从而获得最佳的R2值,使得模型的精度达到最佳。
train_sub <- sample(datasize,round(0.7*datasize))
train_data <- data[train_sub,]
test_data <- data[-train_sub,] #获得训练集与验证集
fit.rf <- randomForest(price~. ,data=train_data,importance=T) #importance设为T,可以采用随机森林自己计算各个变量的重要性
im <- importance(fit.rf,type=2) #将结果保存
pred <- predict(fit.rf,test_data)
obs <- test_data[,'price']
result <- data.frame(obs,pred)
obs <- as.numeric(as.character(result[,'obs']))
pred <- as.numeric(as.character(result[,'pred']))
r <- r2fun(pred,obs) #计算出模型的R2,以此为标准判断模型的性能
print(im) #输出自变量重要性的排名
起初未删除变量时各变量的重要程度排名:
接下来我们便从重要性最低的变量开始,将与其它变量重要性相差较多的变量删除。每删除完一次变量后重新计算各个变量的重要性排名,并重复上述操作。共进行三次变量的删除,四次实验,进行横向比较:
| 调整方式 |
R2 |
| 不删除 |
0.932 |
| 删除四个变量 anonymousFeature14 anonymousFeature10 anonymousFeature9 anonymousFeature3 |
0.935 |
| 删除九个变量 anonymousFeature14,anonymousFeature10,anonymousFeature9,anonymousFeature3,color,transferCount,oiltype,cityId,seatings |
0.942 |
| 删除十一个变量 anonymousFeature14,anonymousFeature10,anonymousFeature9,anonymousFeature3,color,transferCount,oiltype,cityId,seatings anonymousFeature8,carCode |
0.929 |
可以得知,在删除了十一个变量之后,MSE开始减小,因此不宜删除过多变量,本模型最后选择brand(品牌id),serial(车系id),model(车型id),mileage(里程),cityId(城市id),carCode(国标码) ,country(国别),maketype(厂商类型),modelyear(年款),displacement(排量),gearbox(减速箱),oiltype(燃油类型),newprice(新车价),anonymousFeature2(匿名变量2), anonymousFeature5(匿名变量5),anonymousFeature6(匿名变量6),anonymousFeature8(匿名变量8), anonymousFeature11(匿名变量11) ,registerDate_year(注册年份),used_time(使用时间),length(长),width(宽),height(高)这23个变量构建对应的随机森林模型。
mtry参数的调整
mtry代表的是从所有自变量中随机抽取了多少个自变量用于每棵决策树的建立。例如:当mtry值为5时,若此时我们共采取13个自变量建立随机森林,那么每棵决策树建立时便从这13个自变量中随机抽取5个自变量作为分类标准。
对于mtry的调参,我们采用遍历方法,将合理范围内的所有mtry参数遍历一遍,取模型结果最优时的mtry参数值。
我们共有21个自变量,于是将mtry的范围设为(2:20),因为mtry的取值不能小于2,也不能大于等于自变量的总数。
mtry参数调整代码:
###mtry调参
r2list <- c() #利用r2list记录每个不同mtry取值所确定的模型的R2值,以此评判模型的性能
r2best <- 0 #用于存储最大的R2值,即最好的模型性能值
mtrybest <- 0 #记录当模型性能达到最好时mtry所对应的值
r_m <- 0
for(i in 2:20)
{
fit.rf1 <- randomForest(price~. ,data=train_data1,importance=T,proximity=TRUE,ntree=500,mtry=i)
pred1 <- predict(fit.rf1,test_data1)
obs1 <- test_data1[,'price']
result1 <- data.frame(obs1,pred1)
obs1 <- as.numeric(as.character(result1[,'obs1']))
pred1 <- as.numeric(as.character(result1[,'pred1']))
r_m <- r2fun(pred1,obs1)
r2list <- c(r2list,r_m)
if( r_m > r2best) #若当前模型的R2值r_m比r2best所存储的值大,则将r2best的值替换为r_m
{
r2best <- r_m
mtrybest <- i
}
}
若想画出R2随mtry参数变化的曲线图,只需加上下面的代码:
plot(x=c(2:20),y=r2list,xlab='mtry',ylab='R2',main='R2随mtry取值变化图')
在此我们便不一一作展示。
最终所得最佳R2值与所对应mtry值如下表:
| 评价指标 |
R方 | MSE | MAE |
| 测试集 |
0.9541 |
1.8406 |
0.8649 |
maxdepth调参
maxdepth参数的调整过程与mtry基本相同,将范围设为seq(10,100,10)即介于10到100之间,以10为跨度取值。
maxdepth调参代码:
###maxdepth调参
r2list <- c() #记录不同的maxdepth取值所对应的R2
r2best <- 0 #记录R2最大值为多少
maxdepthbest <- 0 #记录R2最大时所对应的maxdepth值
r_d <- 0
for(j in seq(10,100,10))
{
fit.rfd <- randomForest(price~. ,data=train_data,importance=T,proximity=TRUE,ntree=500,mtry=20,max_depth=j)
pred <- predict(fit.rfd,test_data)
obs <- test_data[,'price']
result <- data.frame(obs,pred)
obs <- as.numeric(as.character(result[,'obs']))
pred <- as.numeric(as.character(result[,'pred']))
r_d <- r2fun(pred,obs)
depthlist <- c(depthlist,r_d)
if( r_d > r2best)
{
r2best <- r_d
maxdepthbest <- j
}
}
原理同mtry的调参过程相同,由于时间关系,我们最终并未计算出最终结果。因为数据量较大,模型的构建时间较长,而我们做这个项目的时间有限。感兴趣的小伙伴可以试试噢。
扩展篇
GridSearch方法
上面我们对于mtry与maxdepth的调参运用的方法是先找到mtry的最佳取值,而后将其固定,再进行maxdepth的调参。此种方法虽然比之GridSearch更快,但很容易陷入局部最优。
如同这张图,我们有可能到达了某个小山峰的峰顶,但却不是整个曲面中最高的顶点,这种情况下我们仅达到了局部最优,并不是全局最优。想要达到全局最优我们可以采用GridSearch方法。
那么GridSearch是什么呢?GridSearch的中文直译是网格搜索。这听起来很高大上,但其实原理非常简单,就是将不同参数的遍历循环嵌套,得到最优的参数组合。话不多说,先上代码:
###GridSearch方法
r2list <- c() #记录不同的maxdepth与mtry的参数组合所对应的R2
r2best <- 0 #记录R2最大值为多少
mtrybest <- 0 #记录R2最大时mtry所对应值
depthbest <- 0 #记录R2最大时depth所对应值
r_g <- 0
for(i in 2:20)
{
for(j in seq(10,100,10))
{
fit.rf1 <- randomForest(price~. ,data=train_data1,importance=T,proximity=TRUE,ntree=500,mtry=i,maxdepth=j)
pred1 <- predict(fit.rf1,test_data1)
obs1 <- test_data1[,'price']
result1 <- data.frame(obs1,pred1)
obs1 <- as.numeric(as.character(result1[,'obs1']))
pred1 <- as.numeric(as.character(result1[,'pred1']))
r_g <- r2fun(pred1,obs1)
r2list <- c(r2list,r_m)
if( r_g > r2best)
{
r2best <- r_g
mtrybest <- i
depthbest <- j
}
}
}
可以看到此方法并没有本质上的变化,同样是进行遍历,找出最优的参数。只不过不再是单个参数的遍历,而是两个参数组合的遍历。如这个项目中mtry有19种情况,maxdepth有10种情况,那么他们的参数组合便有190种情情况。这190种情况就像一张大网上的许多小网格。网格搜索便是在这190个小网格中找到让R2最大的小网格,即是mtry与maxdepth的最佳参数组合。这样一来自然能达到全局最优,但同时计算量也大大增加。由于我们设备计算能力的有限,我们并未采取GridSearch方法,有兴趣的小伙伴可以试试噢。
交叉验证
交叉验证是指将数据集分成k份,这k份数据子集轮流作为验证集,其余(k-1)份数据集作为训练集。最终得到k个模型,在做回归分析时将这k个模型的结果平均,这样会使预测值更稳定,也更准确。
附上交叉验证代码:
###交叉验证
CVgroup <- function(k,datasize,seed){
cvlist <- list()
set.seed(seed)
n <- rep(1:k,ceiling(datasize/k))[1:datasize] #将数据分成K份,并生成数据集n
temp <- sample(n,datasize) #把n打乱
x <- 1:k
dataseq <- 1:datasize
cvlist <- lapply(x,function(x) dataseq[temp==x]) #dataseq中随机生成k个随机有序数据列
return(cvlist)
}
k即子集的划分个数,datasize为数据集的大小,seed是自己设置的随机种子。分成k份便是k折交叉验证。
这个项目也可以采用k折交叉验证。但同样因为设备计算能力的有限以及时间的有限,我们并未采用交叉验证的方法。感兴趣的小伙伴可以自己尝试噢。