前端学数据结构与算法（五）：二叉树特性及从零实现二叉搜索树

前言

之前的章节主要介绍的都是线性的数据结构(队列下章介绍)，从这章开始将介绍01世界里另一个更普遍与常用的数据结构-树，这也是比线性数据结构更复杂，更好玩一种数据结构。树的结构有非常多种，二叉的、多叉的、平衡的、有序的等等。这一章上半部分主要介绍二叉树及其相关定义，后半部分从底层实现一颗二叉搜索树，包括它的增、删、查等，最后谈谈它的性能以及优缺点，从完整的角度理解这种数据结构。

什么是二叉树

就像是自然界里的树一样，从树干上分出树杈，从树杈到树梢，只不过说二叉树指定的就是每次分出两个杈而已。在01世界里是这么展现的：

image

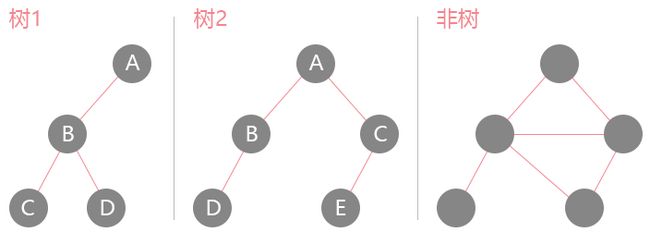
树的种类很多，首先来看看它们对应的名词：

• 根节点：树1和树2的节点A都是该树的根节点。
• 父节点：树1里节点A是B的父节点，B又是C和D的父节点。
• 左/右孩子：树2里B和C是A的左右孩子，D又是B的左孩子节点。
• 兄弟节点：当两个节点的父节点相同时，他们之前就是兄弟关系，例如树2里的B和C。
• 左/右子树：以左右孩子为起点，形成的完整的子树，就是其父节点的左右子树，如树2里BD形成的二叉树就是A的左子树，CE就是其右子树。
• 叶子节点：一棵树里位于最底层的节点，也就是没有孩子节点的节点，就是叶子节点，如树2里的DE。
• 路径：从一个节点到另外一个节点时，其间经过节点形成的线路就是路径。
• 高度：某节点到叶子节点的路径，例如树1里节点A的高度就是2，B的高度是1。
• 深度：根节点到某个节点的路径，例如树2里节点A的深度是0，节点B和C的深度是1，
• 层数：节点位于整棵树的第几层，值为节点的深度值加一。

二叉搜索树

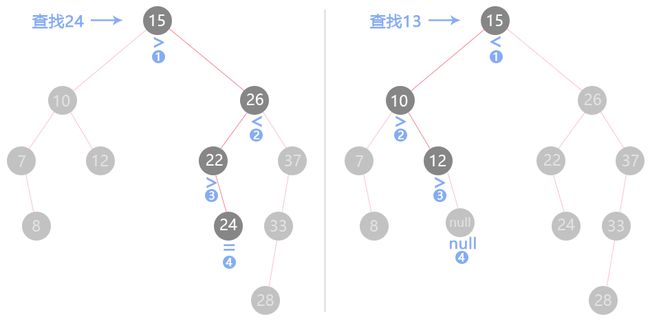
顾名思义是二叉树的一种，专注于检索，特点是让节点按照一定的规律摆放，从而让搜索某个节点特别的高效，例如下图就是一颗二叉搜索树：

image

如果以根节点左右划分这棵树，左子树里的节点全部小于根节点，右子树全部大于根节点，而且无论以哪个节点作为根节点来划分，规律亦是如此。

为什么要这么排列？当我们需要检索一个值时，如果大于该节点就去右子树查找，如果小于就去该节点的左子树查找，每次都可以过滤掉一半查找返回。需要说明的就是，二叉搜索树里每个节点的值必须具备可比较性。例如图中一共有15个数字，找到数字33根据比对只需要查找4次即可，这也是为什么叫它二叉搜索树的原因。

满二叉树与完全二叉树

image

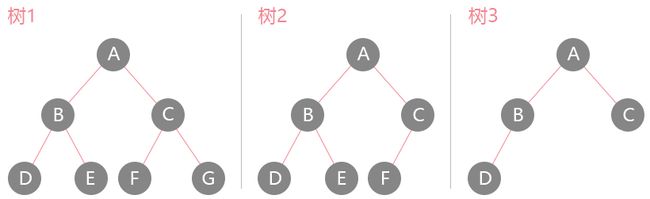
这是二叉树里面排列比较特殊两种，上图中树1就是一颗满二叉树，它的特点是叶子节点全部都在最底层，而且除了叶子节点之外，每个节点都有左右两个孩子，排的满满当当；上图中树2和树3就是一颗完全二叉树，它的特点是最底下一层的叶子节点全部朝左边摆放，并且如果最底层的叶子节点没了的话，剩下的节点是一颗满二叉树。同理满二叉树又是一颗特殊的完全二叉树。

为什么要这么区分？因为一颗完全二叉树是可以用数组来存储的，而不会有任何内存空间的浪费。树2我们可以用数组来表示：

const tree2 = ['A', 'B', 'C', 'D', 'E', 'F']

如根节点A的下标是0，那么它的左孩子就是2 * 0 + 1，右孩子就是2 * 0 + 2。以此类推，0替换为i后，就可以表示每个节点的左右孩子，而不需要常规节点类，使用两个左右指针去指向左右孩子，这也是一种更高效的存储方案。例如之后章节还会介绍另一种二叉树-二叉堆，它无论何时都是一颗完全二叉树，所以它的最优存储方案就是用数组。

实现二叉搜索树

还是首先初始化两个类，一个节点类，一个树类：

class TreeNode {
  constructor(val) {
    this.val = val
    this.left = null // 左孩子
    this.right = null // 右孩子
  }
}

class BST {
  constructor() {
    this.root = null // 根节点
  }
}

增

根据二叉搜索树的定义，所以需要保证无论往这颗树上增加多少个节点，都需要保证其定义不被破坏。当遇到一个新的节点需要插入时，我们可以与根节点进行比较，如果比根节点值大就放入右子树内，如果比根节点值小就放入左子树内，使用这样的插入规则，逐层往下，总会遇到一个节点的孩子为空，将新节点设置为其新的孩子节点即可。

image

class BST {
  ...
  add(val) { // 不考虑重复值的情况
    const _helper = (node, val) => {
      if (node === null) { // 如果某个节点的孩子节点为空，创建新节点返回即可
        return new TreeNode(val)
      }
      if (node.val > val) { // 如果当前节点值比val大，新节点需要放在其左子树里
        node.left = _helper(node.left, val) // 以当前节点左孩子为起点，返回新的左孩子节点
        return node // 返回新的节点
      } else if (node.val < val) { // 同理
        node.right = _helper(node.right, val) // 同上
        return node
      }
    }
    this.root = _helper(this.root, val)
    // 从根节点开始插入val, 返回新的根节点
  }
}

查

根据二叉搜索树的特性从根节点开始比较，还是逐层进行递归，如果根据规则最后遇到了空节点，那说明这颗树里没有这个节点。

image

class BST {
  ...
  contains(val) {
    const _helper = (node, val) => {
      if (node === null) { // 如果到头也没右找到
        return false
      }
      if (node.val === val) { // 正好找到
        return true
      }
      if (node.val > val) { // 如果比当前节点小
        return _helper(node.left, val) // 去左子树里找
      } else { // 如果比当前节点大
        return _helper(node.right, val) // 去右子树里找 
      }
    }
    return _helper(this.root, val) // 从根节点开始
  }
}

删

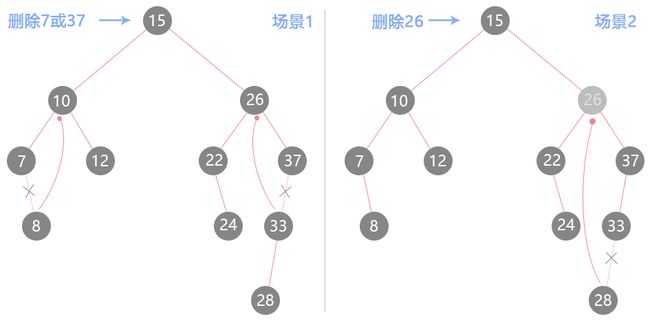
二叉搜索树最麻烦的操作也就是删除，因为在删除了一个节点之后，原来位置的节点并不会空着，必须找到替代的节点续上才行。怎么续上而又保持二叉搜索树的定义又分为几种情况：

image

• 1. 一边有孩子节点

场景1里面的两种场景，将另一边的孩子节点续上即可。

• 2. 两边都有孩子节点

场景2里面也有两种处理方式，一种是在待删除节点的左子树里面找到最大的值替代(24)，然后切断其链接；另一种是在待删除的右子树里面找到最小值替代(28)，然后切断其链接。

为了应对场景2，我们需要找到指定节点树的最小或最大节点，然后还需要在指定节点树里删除最小或最大的节点，所以先把辅助方法写出来以便后面使用，这里采用在右子树里找最小值的方案：

class BST {
  ...
    _minimum(node) { // 返回指定节点树的最小值节点
    if (node.left === null) {
      return node
    }
    return this._minimum(node.left)
  }
  
  _removeMin(node) { // 删除指定节点树的最小节点
    if (node.left === null) {
      const rightNode = node.right
      node.right = null
      return rightNode
    }
    node.left = this._removeMin(node.left)
    return node
  }
}

根据二叉搜索树的特性，指定树的最小值一定就是沿着左边一直找，最后找到的那个非空节点；而删除指定树的最小值节点，也只需要用被删除节点的右子树续上即可。

class BST {
  ...
  remove(val) { // 删除指定值
    const _helper = (node, val) => {
      if (node === null) { // 如果到底了也没有
        return node // 直接返回空
      }
      if (node.val === val) { // 如果正好找到了
        if (node.left === null) { // 左孩子为空时，让右孩子续上
          const rightNode = node.right
          node.right = null
          return rightNode
        } else if (node.right === null) { // 右孩子为空时，让左孩子续上
          const leftNode = node.left
          node.left = null
          return leftNode
        } else { // 如果左右都右孩子
          const successor = this._minimum(node.right) // 在右子树里找最小的节点
          node.right = this._removeMin(node.right) // 并且删除右子树里最小的节点
          successor.left = node.left // 让新节点指上之前的左孩子
          successor.right = node.right // 让新节点指上之前的右孩子
          return successor // 返回新节点
        }
      } else if (node.val > val) { // 比值递归
        node.left = _helper(node.left, val)
        return node
      } else { // 比值递归即可
        node.right = _helper(node.right, val)
        return node
      }
    }
    this.root = _helper(this.root, val) // 从根节点开始，删除指定值没返回值
  }
}

从上面的代码可以看出，删除二叉搜索树的某个节点还是很麻烦的，分的情况比较多。但如果把几种对应场景的应对思路理清楚后，看懂代码和写出对应的逻辑其实并太难。

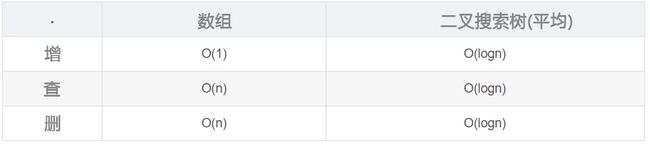
性能比对

存储需要占用额外空间去保存节点的指针，就是简单的增删查就这么的复杂，这还不包括更麻烦的其他操作，这么折腾是为了什么？没错，一切为了性能服务，假如从100万条数据里查找对应数据，数组需要O(n)的复杂度，而二叉搜索树平均只需要O(logn)即可，也就是查找20次即可找到，当树的节点数量每次乘2的倍增时，查找的次数只是加1而已。而从100万条数据里移除某条数据时，数组需要O(n)的搬家操作，而二叉树每次也是只需要O(logn)即可完成操作。

image

最后

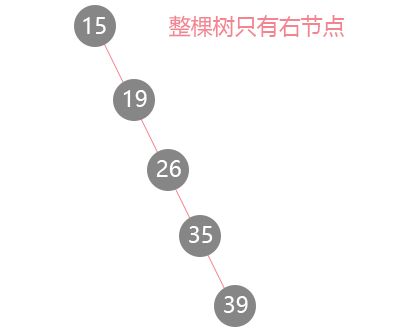
为什么在最后的比对性能中二叉树各项需要加上平均二字了？因为会出现极端的情况，如一颗二叉树是这样的：

image

所以二叉搜索树的缺点也很明显，极端情况下会退化成了链表，这时它的任何操作将会变成O(n)。为了避免这种情况出现，就需要使用自平衡的二叉搜索树，也就是之后会介绍的AVL树和大名鼎鼎的红黑树，而这两种树结构太过复杂，再介绍完其他树后再做介绍吧。本章github源码