空洞卷积的理解
一、空洞卷积的本质
空洞卷积(dilated convolution)在标准卷积里注入空洞,增加感受野(reception filed)。
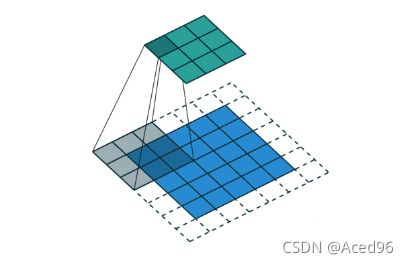
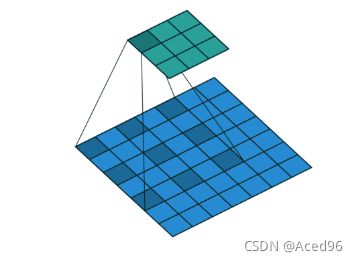
空洞卷积比普通卷积多了个超参数称为dilation rate,指的是kernel的间隔数量。普通卷积的dilation rate为1。
普通卷积:
空洞卷积:
二、空洞卷积的优点
关于传统深度卷积的up-sampling和pooling layer的缺点
2.1 up-sampling(放大特征图)
up-sampling(放大特征图):线性插值、反卷积(deconvolution)、unpooling。
-
unpooling:恢复max的位置,其余部分补零
-
deconvolution(反卷积):先对input补零,再conv
-
插值方法:双线性插值等;
2.2 pooling-layer(缩小特征图)
pooling-layer(缩小特征图):max pooling、average pooling。
**池化层本质:**在精简feature map数据量的同时,最大化保留空间信息和特征信息。
2.3 主要问题
1)上采样+池化层的参数不可学习
2) 小物体信息无法重构(假设有4个池化层,则任何小于[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w0WTggNZ-1630381240320)(https://math.jianshu.com/math?formula=2%5E4)]=16 pixel的物体在理论上无法重建。)
3) 内部数据结构丢失,空间层级化信息丢失。
图像分割流程:
-
图像输入到CNN(FCN)中,FCN先对图像做卷积再池化(降低图像尺寸的同时增大每个像素的感受野)。
-
由于图像分割预测是像素级,需要将池化后较小的特征图上采样到原始的图像尺寸来进行预测。
-
FCN中两个关键:池化减小图像尺寸增大感受野+ 上采样扩大图像尺寸
问题:在先减小再增大尺寸过程中,肯定有一些信息损失掉了。可以不通过池化也能有较大感受野,看到更多信息吗? 空洞卷积。
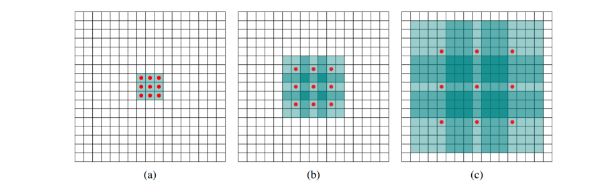
(a):普通
(b):k为3x3,空洞为1 ------>感受野为7x7
(c): 感受野为15x15
2.4 空洞卷积
**空洞卷积的好处:**在不做池化损失信息的情况下,加大了感受野,使得内部数据结构得到保留。
三、空洞卷积存在的问题
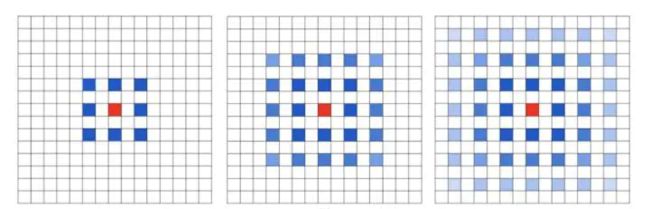
潜在问题1:The Gridding Effect(网格效果)
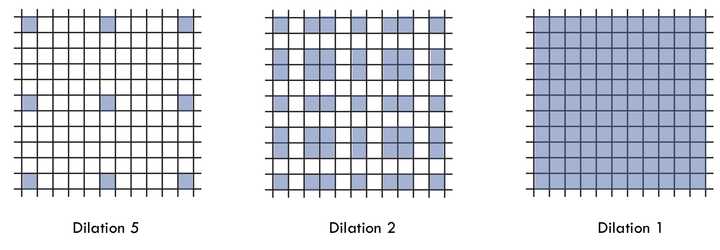
例如:假设我们仅仅多次叠加dilation rate=2的 3x3 kernel ,会出现以下问题:
我们的卷积核是不连续的,也就是说特征图中不是所有的pixel都用来计算了。这里将信息看作checker-board的方式会损失信息的连续性。这对像素密集型的任务来说是致命的。
潜在问题2:长期的信息可能不相关。
从空洞卷积的设计背景来看,这样的设计是用来获取long-ranged 信息。光采用大dilation rate的信息或许只对一些大物体分割有效果,对小物体来说有弊无利。
如何同时处理不同大小的物体关系,是设计好dilated convolution网络的关键。
四、通过标准化设计:Hybrid Dilated Convolution(HDC)
针对上一节提到的问题,图森组的文章提出好的解决方案,设计了一个称之为HDC的设计结构。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PLjKW61c-1630381240337)(https://math.jianshu.com/math?formula=%5Cbullet%20)] 第一个特性:叠加捐的的dilation rate不可能有大于1的公约数。比如[2,4,6]则不是好的三层卷积,依然会出现gridding effect。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mMMsGUDG-1630381240340)(https://math.jianshu.com/math?formula=%5Cbullet%20)] 第二个特性: 将dilation rate设计成锯齿状结构,例如[1,2,5,1,2,5]循环结构。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l1C1BxLi-1630381240343)(https://math.jianshu.com/math?formula=%5Cbullet%20)] 第三个特性: 满足下面一下这个式子
![]()
r i : r_i : ri: 第i层的dilation rate
M i : M_i : Mi: 在第i层的最大dilation rate
假设总共有 n 层, 默认 M n = r n M_n=r_n Mn=rn.
假设我们应用于 kernel 为 k x k 的话,我们的目标则是 M 2 ≤ K M_2 ≤ K M2≤K ,这样我们至少可以用dilation rate 1 即 standard convolution 的方式来覆盖掉所有洞。
一个简单的例子: dilation rate [1, 2, 5] with 3 x 3 kernel (可行的方案)
而这样的锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求(小 dilation rate 来关心近距离信息,大 dilation rate 来关心远距离信息)。
这样我们的卷积依然是连续的也就依然能满足VGG组观察的结论,大卷积是由小卷积的 regularisation 的 叠加。
以下的对比实验可以明显看出,一个良好设计的 dilated convolution 网络能够有效避免 gridding effect.

ffect.